- •2. Источники эдс и источники тока и их внешние характеристики.
- •4. Расчет сложных электрических цепей методом уравнений Кирхгофа.
- •5. Расчет сложных электрических цепей методом контурных токов.
- •6. Расчет сложных электрических цепей методом узловых потенциалов.
- •7. Расчет параллельных электрических цепей методом двух узлов.
- •8. Параметры синусоидального тока и их отображение на временной диаграмме. Угол сдвига фаз.
- •9. Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление. Фазовые соотношения между напряжением и током.
- •10. Конденсатор в цепи переменного тока. Емкостное сопротивление. Фазовые соотношения между напряжением и током.
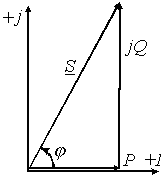
- •12. Изображение синусоидальных электрических величин в комплексной форме. Комплексные амплитуды и комплексы электрических величин. Векторные диаграммы электрических величин на комплексной плоскости.
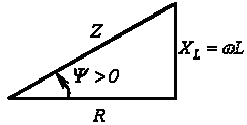
- •14. Последовательная цепь r, l на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
- •15. Последовательная цепь r, c на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
- •16. Последовательная цепь r, l, c на переменном токе: векторная диаграмма тока и напряжений. Реактивное сопротивление цепи. Резонанс напряжений.
- •17. Разветвленные электрические цепи переменного тока: комплексная проводимость последовательной ветви r, l, треугольник проводимостей, эквивалентная параллельная схема с проводимостями.
- •18. Параллельная электрическая цепь из конденсатора и катушки индуктивности: эквивалентная параллельная схема, векторная диаграмма токов. Резонанс токов.
- •20. Коэффициент мощности. Повышение коэффициента мощности компенсацией сдвига фаз.
- •23. Гармонический анализ несинусоидального периодического тока: разложение в тригонометрический ряд, параметры гармоник, параметры несинусоидального тока.
- •25. Уравнения четырехполюсника в разных формах. Экспериментальное определение коэффициентов четырехполюсника формы а из опытов холостого хода и короткого замыкания.
- •26. Уравнения длинной линии с потерями в показательной форме. Коэффициент отражения.
- •27. Расчет переходных процессов классическим методом: определение независимых условий, составление характеристического уравнения его решение, определение постоянных интегрирования.
- •28. Расчет переходных процессов операторным методом: операторная схема, операторные изображения электрических величин и параметров цепей, переход к функции времени по формуле разложения.
- •30. Графические методы расчета последовательных нелинейных электрических цепей постоянного тока.
- •31. Графические методы расчета параллельных нелинейных электрических цепей методом двух узлов.
- •33. Расчет последовательной магнитной цепи.
- •34. Расчет параллельной магнитной цепи методом двух узлов.
14. Последовательная цепь r, l на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
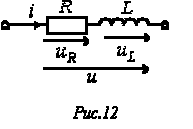
если
в такой ветви течет ток
![]() ,
то падение напряжения будет складываться
из:
,
то падение напряжения будет складываться
из: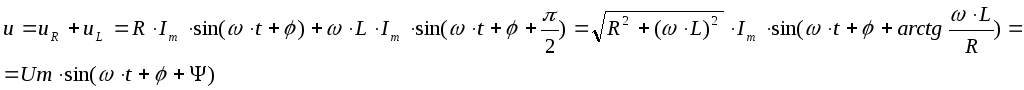
где
![]() ;
приведенному выше уравнению можно
поставить в соответствие выражение:
;
приведенному выше уравнению можно
поставить в соответствие выражение:![]() ,
которое наглядно демонстрируют векторные
диаграммы, называемые соответственнотреугольником
напряжений и
треугольником сопротивлений,:
,
которое наглядно демонстрируют векторные
диаграммы, называемые соответственнотреугольником
напряжений и
треугольником сопротивлений,:
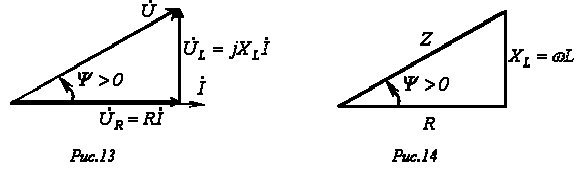
-
закон Ома в комплексной форме:
![]()
15. Последовательная цепь r, c на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
если
в такой ветви течет ток
![]() ,
то падение напряжения будет складываться
из:
,
то падение напряжения будет складываться
из:
где
![]() ;
приведенному выше уравнению можно
поставить в соответствие выражение:
;
приведенному выше уравнению можно
поставить в соответствие выражение:![]() ,
которое наглядно демонстрируют векторные
диаграммы, называемые соответственнотреугольником
напряжений и
треугольником сопротивлений,:
,
которое наглядно демонстрируют векторные
диаграммы, называемые соответственнотреугольником
напряжений и
треугольником сопротивлений,:


-
закон Ома в комплексной форме:
![]()
16. Последовательная цепь r, l, c на переменном токе: векторная диаграмма тока и напряжений. Реактивное сопротивление цепи. Резонанс напряжений.
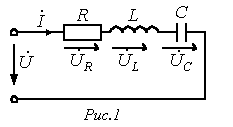
падение
напряжения на цепи:
![]() ,
где:
,
где:![]() ,
а
,
а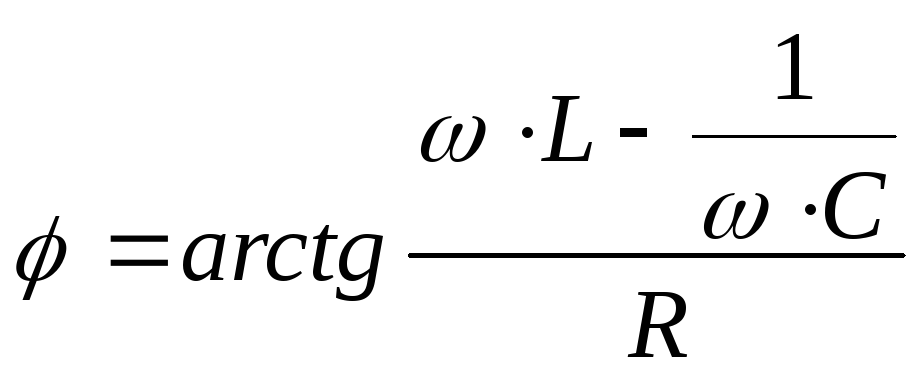 .
В зависимости от соотношения величин
.
В зависимости от соотношения величин![]() и
и![]() возможны
три различных случая:
возможны
три различных случая:
-
в цепи преобладает индуктивность, т.е.
![]() ,
а следовательно
,
а следовательно![]() .
Этому режиму соответствует векторная
диаграмма нарисунке
а.
.
Этому режиму соответствует векторная
диаграмма нарисунке
а.
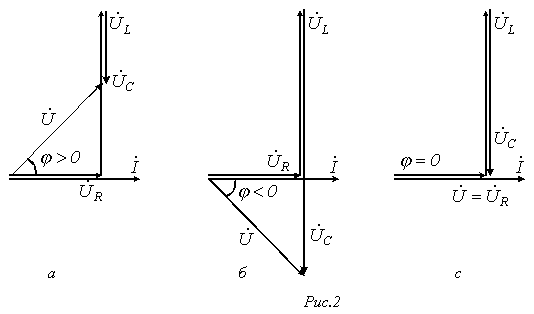
-
в цепи преобладает емкость, т.е.
![]() ,
а значит,
,
а значит,![]() .
Этот случай отражает векторная диаграмма
нарисунке
б.
.
Этот случай отражает векторная диаграмма
нарисунке
б.
-
![]() - случай резонанса напряжений (рисунок
в).
- случай резонанса напряжений (рисунок
в).
Условие
резонанса напряжений:
![]() ,
при котором
,
при котором![]() .
При резонансе напряжений или режимах,
близких к нему, ток в цепи резко возрастает.
В теоретическом случае при R=0 его величина
стремится к бесконечности. Соответственно
возрастанию тока увеличиваются напряжения
на индуктивном и емкостном элементах,
которые могут во много раз превысить
величину напряжения источника питания.
Физическая сущность резонанса заключается
в периодическом обмене энергией между
магнитным полем катушки индуктивности
и электрическим полем конденсатора,
причем сумма энергий полей остается
постоянной.
.
При резонансе напряжений или режимах,
близких к нему, ток в цепи резко возрастает.
В теоретическом случае при R=0 его величина
стремится к бесконечности. Соответственно
возрастанию тока увеличиваются напряжения
на индуктивном и емкостном элементах,
которые могут во много раз превысить
величину напряжения источника питания.
Физическая сущность резонанса заключается
в периодическом обмене энергией между
магнитным полем катушки индуктивности
и электрическим полем конденсатора,
причем сумма энергий полей остается
постоянной.
- резонансными кривыми называются зависимости тока и напряжения от частоты:
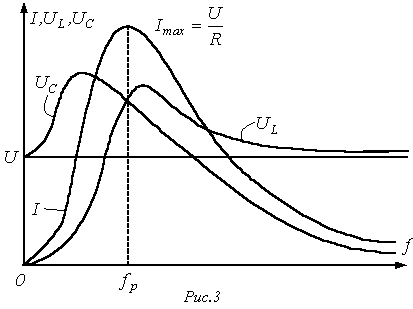
17. Разветвленные электрические цепи переменного тока: комплексная проводимость последовательной ветви r, l, треугольник проводимостей, эквивалентная параллельная схема с проводимостями.
![]()
-
полное
сопротивление
такой цепи:
![]() ;
;
-
полная
проводимость:
![]() ;
;
-
преобразуя далее:
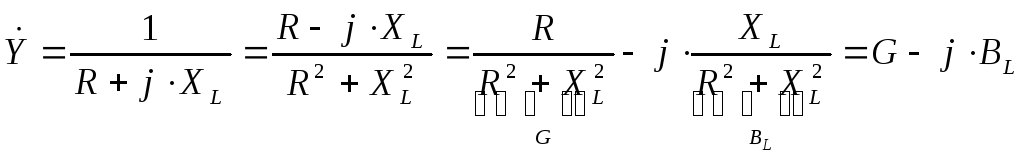 ,
получим выражения дляG
(активной
проводимости
цепи RL)
и ВL
(индуктивной
проводимости
цепи RL);
,
получим выражения дляG
(активной
проводимости
цепи RL)
и ВL
(индуктивной
проводимости
цепи RL);
-
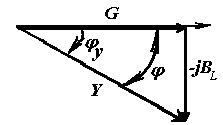
при изображении треугольника проводимостей
на комплексной площади откладывают
активную, индуктивную и полную
проводимости: ( см. рис.)
![]() и
и![]()
- последовательную схему соединения R и L можно заменить на параллельную преобразовав ток через цепь как сумму активного и реактивного тока:
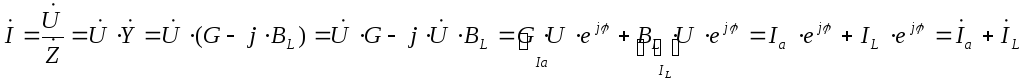
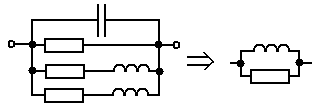
производить расчеты разветвленных схем удобно, приводя их к эквивалентной параллельной:
18. Параллельная электрическая цепь из конденсатора и катушки индуктивности: эквивалентная параллельная схема, векторная диаграмма токов. Резонанс токов.
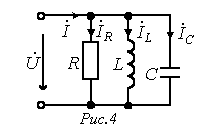
-
комплекс общего тока через такую ветвь:
![]() ;
;
-
проводимость такой цепи:
![]() ,
а
,
а![]()
,
В
зависимости от соотношения величин
![]() и
и
![]() возможны
три различных случая.
возможны
три различных случая.
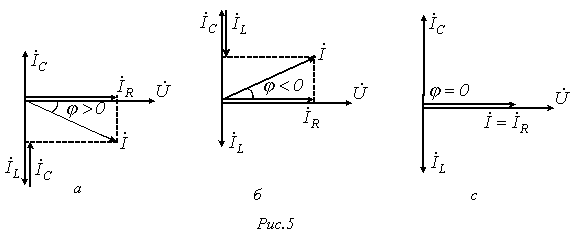
-
в цепи преобладает индуктивность, т.е.
![]() ,
а следовательно,
,
а следовательно,![]() .
Этому режиму соответствует векторная
диаграмма нарисунке
а.
.
Этому режиму соответствует векторная
диаграмма нарисунке
а.
-
в цепи преобладает емкость, т.е.
![]() ,
а значит,
,
а значит,![]() .
Этот случай иллюстрирует векторная
диаграмма нарисунке
б.
.
Этот случай иллюстрирует векторная
диаграмма нарисунке
б.
-
и
![]() - случай резонанса токов (рисунок
в).
- случай резонанса токов (рисунок
в).
Условие
резонанса токов
![]() или
или![]() .
Таким образом, при резонансе токов
входная проводимость цепи минимальна,
а входное сопротивление, наоборот,
максимально. В частности при отсутствии
в цепи на рисунке резистораR
ее входное сопротивление в режиме
резонанса стремится к бесконечности,
т.е. при резонансе токов ток на входе
цепи минимален.
.
Таким образом, при резонансе токов
входная проводимость цепи минимальна,
а входное сопротивление, наоборот,
максимально. В частности при отсутствии
в цепи на рисунке резистораR
ее входное сопротивление в режиме
резонанса стремится к бесконечности,
т.е. при резонансе токов ток на входе
цепи минимален.
Приведенное условие резонанса справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов.
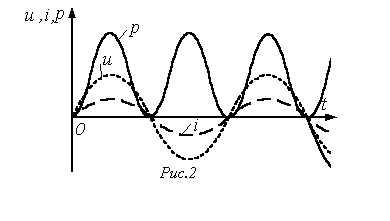
19. Мощность в электрической цепи переменного тока: мгновенная мощность в элементах R, L, C. Реактивная мощность индуктивности и емкости. Треугольник мощностей. Активная, реактивная, полная и комплексная мощности всей цепи.
-
интенсивность передачи или преобразования
энергии называется мощностью:
![]()
-
мгновенное
значение мощности
в электрической цепи:
![]() ,
приняв начальную фазу напряжения за
нуль, а сдвиг фаз между напряжением и
током за
,
приняв начальную фазу напряжения за
нуль, а сдвиг фаз между напряжением и
током за![]() ,
получим:
,
получим:
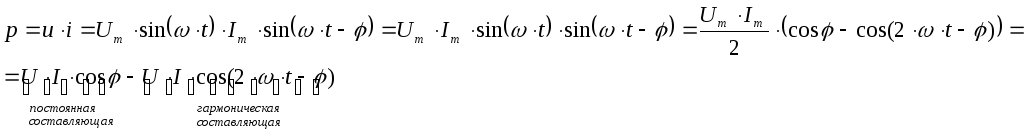
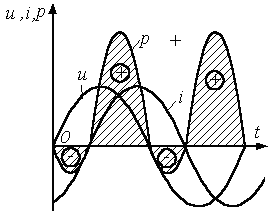
Т.о., мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.
Когда мгновенная мощность отрицательна, а это имеет место (см. рисунок), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.
Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника;
-
энергия, отдаваемая источником
двухполюснику в течение времени t
равна
![]() .
.
-
среднее за период значение мгновенной
мощности называется активной
мощностью:
![]() ,
[Вт]; Учитывая, что
,
[Вт]; Учитывая, что
![]() ,
получим:
,
получим:![]() .
Активная мощность, потребляемая пассивным
двухполюсником, не может быть отрицательной
(иначе двухполюсник будет генерировать
энергию), поэтому
.
Активная мощность, потребляемая пассивным
двухполюсником, не может быть отрицательной
(иначе двухполюсник будет генерировать
энергию), поэтому![]() ,
т.е. на входе пассивного двухполюсника
,
т.е. на входе пассивного двухполюсника![]() .
СлучайР=0,
.
СлучайР=0,
![]() теоретически возможен для двухполюсника,
не имеющего активных сопротивлений, а
содержащего только идеальные индуктивные
и емкостные элементы.
теоретически возможен для двухполюсника,
не имеющего активных сопротивлений, а
содержащего только идеальные индуктивные
и емкостные элементы.
-
мощность
на резисторе
(идеальном активном сопротивлении)
потребляется только активная, т.к. ток
и напряжение совпадают по фазе:
![]()
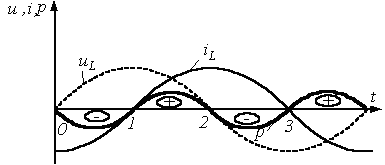
- мощность на катушке индуктивности (идеальной индуктивности) не потребляется:
Т.к.
ток отстает от напряжения по фазе на
![]() ,
то:
,
то:
![]() ;
На участке
1-2 (см. рис.) энергия, запасаемая в магнитном
поле катушки, нарастает. На участке 2-3
- убывает, возвращаясь в источник.
;
На участке
1-2 (см. рис.) энергия, запасаемая в магнитном
поле катушки, нарастает. На участке 2-3
- убывает, возвращаясь в источник.
- мощность на конденсаторе (идеальной емкости) также не потребляется:
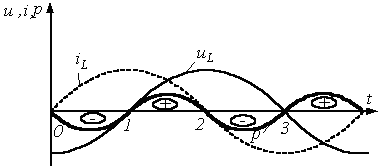
Ток
здесь опережает напряжение, поэтому
![]() ,
и
,
и
![]() .
Т.о., в катушке индуктивности и конденсаторе
не происходит необратимого преобразования
энергии в другие виды энергии. Здесь
происходит только циркуляция энергии:
электрическая энергия запасается в
магнитном поле катушки или электрическом
поле конденсатора на протяжении четверти
периода, а на протяжении следующей
четверти периода энергия вновь
возвращается в сеть. В силу этого катушку
индуктивности и конденсатор называют
реактивными элементами, а их сопротивления
ХL
и ХС
,
в отличие от активного сопротивления
R
резистора, –
реактивными.
.
Т.о., в катушке индуктивности и конденсаторе
не происходит необратимого преобразования
энергии в другие виды энергии. Здесь
происходит только циркуляция энергии:
электрическая энергия запасается в
магнитном поле катушки или электрическом
поле конденсатора на протяжении четверти
периода, а на протяжении следующей
четверти периода энергия вновь
возвращается в сеть. В силу этого катушку
индуктивности и конденсатор называют
реактивными элементами, а их сопротивления
ХL
и ХС
,
в отличие от активного сопротивления
R
резистора, –
реактивными.
-
интенсивность поступления энергии в
магнитное поле катушки или электрическое
поле конденсатора называется реактивной
мощностью:
![]() ,
[ВАр]. Она положительна при отстающем
токе (индуктивная нагрузка-
,
[ВАр]. Она положительна при отстающем
токе (индуктивная нагрузка-![]() )
и отрицательна при опережающем токе
(емкостная нагрузка-
)
и отрицательна при опережающем токе
(емкостная нагрузка-![]() ).
).
-
реактивная
мощность на индуктивности:
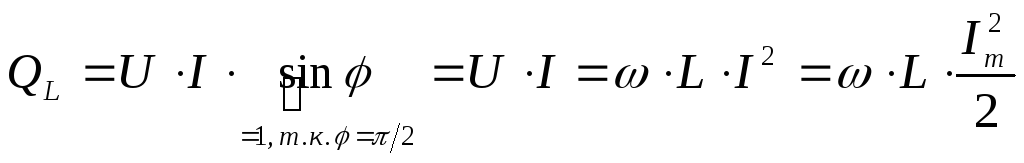
-
реактивная
мощность на конденсаторе
:
![]()
-
полная мощность:
![]() ,
[ВА]
,
[ВА]
-
комплексная мощность:
активную,
реактивную и полную мощности можно
определить, пользуясь комплексными
изображениями напряжения и тока. Если
![]() ,
а
,
а![]() ,
то комплекс полной мощности:
,
то комплекс полной мощности:
![]() ;
;
-
треугольник
мощностей
–
отображение комплексных значений
мощностей на комплексной плоскости
(при
![]() имеем следующее отображение):
имеем следующее отображение):