Дисциплина «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»

СОДЕРЖАНИЕ

1. Основные понятия, параметры и законы электрических цепей: элементы электрических цепей и их параметры; условные графические обозначения параметров; схемы замещения и топологические понятия: ветвь, узел, контур; законы Ома и Кирхгофа

- Электрическая цепь – совокупность электрических элементов, соединенных проводниками, в которой имеется источник электроэнергии и протекает электрический ток.

- Резистивные элементы – элементы, потребляющие активную электроэнергию, (R, [Ом]) - ,- модель;

- Индуктивный элемент – катушки индуктивности, трансформаторы, дроссели, (L, [Гн]) - ,,- модель;

- Емкостные элементы – конденсаторы, линии электропередач, (С, [Ф]), ,- модель;

- Электрический ток – направленное движение электрических зарядов, (I, [A]), ;

- Напряжение – разность потенциалов между двумя точками цепи, (U, [B]), ,;

- Схема замещения эл. цепи – изображение элементов эл. цепи с помощью УГО линий вместо проводников;

- Ветвь – участок эл. цепи, где протекает ток одной величины;

- Узел – точка схождения более чем двух узлов;

- Контур – замкнутый участок цепи;

- закон Ома для участка цепи: ;

- закон Ома для участка цепи с ЭДС: ;

- I-й закон Кирхгофа: сумма всех токов, сходящихся в любом узле электрической цепи, равна нулю - ;

- II-й закон Кирхгофа: алгебраическая сумма электродвижущих сил какого либо замкнутого контура электрической цепи равна алгебраической сумме падений напряжений в нем - ;

2. Источники эдс и источники тока и их внешние характеристики.

- источник ЭДС – источник с неизменной ЭДС, ,- внешняя характеристика, реальный источник ЭДС имеет внутреннее сопротивление -,;

- источник тока – источник с постоянным значением тока в независимости от нагрузки, ,, реальный источник тока,.

3. Преобразование схем: с последовательным, параллельным и смешанным соединением элементов. Преобразование треугольника сопротивлений в звезду сопротивлений и обратно – из звезды сопротивлений – в треугольник сопротивлений.

- последовательное - ;

- параллельное - ;

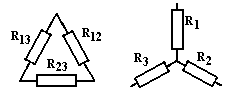
- Δ→Y - ; ;;

- Y→Δ - ; ;;

4. Расчет сложных электрических цепей методом уравнений Кирхгофа.

Метод применяется при рассмотрении сложных схем с несколькими источниками. Кол-во всех ур-й равно кол-ву токов.

- составляются ур-я по I-му з-ну Кирхгофа для узлов (один узел заземляется (см. рис. d), потенциал его равен нулю и для него уравнение не составляется (направления токов проставляем произвольно; ток, втекающий в узел “+”, вытекающий “-”):

- остальные ур-я составляется по II-му з-ну Кирхгофа для контуров (контуры обходим по часовой стрелке; при совпадении тока с обходом – “+”, при несовпадении – “-”):

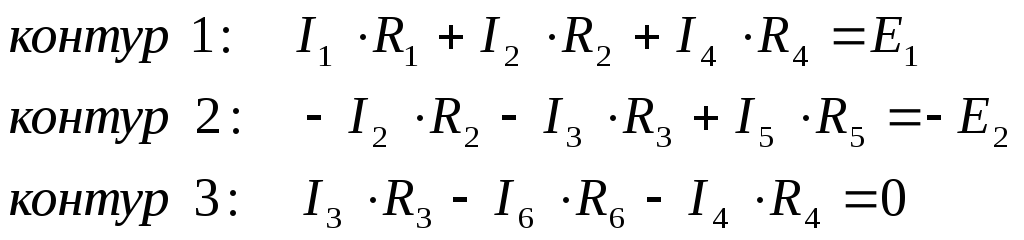
- из значений ЭДС и коэффициентов токов составляются матрицы:

;

- матрица искомых токов ветвей:

5. Расчет сложных электрических цепей методом контурных токов.

Заключается в вычислении расчетных контурных токов, с помощью которых потом вычисляются токи ветвей (см. рис. выше).

- расставляются произвольно токи ветвей и контурные;

- составляются ур-я по II-му з-ну Кирхгофа для контурных токов;

- из значений ЭДС и коэффициентов контурных токов составляются матрицы:

;

- матрица искомых контурных токов: ;

- из контурных токов находятся токи ветвей:

; ;;;;;

6. Расчет сложных электрических цепей методом узловых потенциалов.

Назначаются узлы с неизвестными потенциалами (потенциал d=0 (см. рис. выше).

- составляются ур-я по I-му з-ну Кирхгофа для узловых потенциалов:

- составляем матрицы коэффициентов правой и левой частей ур-й:

;

- матрица искомых узловых потенциалов: ;

- токи ветвей находятся как:

; ;;;;;

7. Расчет параллельных электрических цепей методом двух узлов.

Метод применяется в случае, когда в одной из ветвей необходимо рассчитать ток при нескольких режимах работы. Т.о. расчет выполняют для одной ветви (для простоты расчетов выбирают ветвь без источника питания).

- относительно выбранной ветви вся схема рассматривается как двухполюсник, в котором: ; на рис:R₃ заменено разрывом.

- вычисляется как напряжение между выбранными узлами;

- вычисляется как сопротивление схемы относительно выбранных зажимов (точки в виде звезды сопротивлений необходимо преобразовать в треугольник)

; ;;;;;

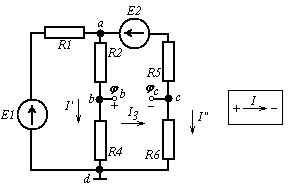
8. Параметры синусоидального тока и их отображение на временной диаграмме. Угол сдвига фаз.

- мгновенные значения: ;;

- ; разность фаз::- напряжение опережает ток

- напряжение отстает от тока

- действующее значение переменного тока – это значение переменного тока, равное такому значению постоянного, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и переменный:

- на временных диаграммах начальная фаза обозначается стрелкой, направленной от начала периода к началу координат. Угол φ показывается от начала периода напряжения к началу периода тока.