2.3. Пассивные элементы r, l, c в цепи синусоидального тока
2.3.1. Идеальный резистивный элемент (ИРЭ)
Мгновенное значение напряжения на ИРЭ:
.
Ток, протекающий через ИРЭ:
;
.
Т.о. напряжение и ток на ИРЭ всегда совпадают по фазе:
Комплексное
сопротивление
.
- закон
Ома в комплексной форме для ИРЭ.
Сопротивление у ИРЭ активное. Активная мощность оценивает интенсивность необратимого процесса преобразования электроэнергии в другие виды энергии.
Мгновенная мощность:
;
,
где
– действующие значения напряжения и
тока.
Среднее значение мощности на ИРЭ:
.
2.3.2. Идеальный ёмкостный элемент (иеэ)
Мгновенное значение напряжения на ИЕЭ:
.
Ток, протекающий через ИЕЭ:
Тогда
– ток
опережает напряжение на
.
Комплексное сопротивление ИЕЭ:
,
где
- емкостное сопротивление.
- закон
Ома в комплексной форме для ИЕЭ.
Мгновенная мощность:
;
.
Средняя мощность:
.
Энергетические процессы в ИЕЭ носят обменный характер с двойной частотой по отношению к частоте цепи.
Процессы обмена энергией между источником и приемником – реактивные процессы.
Сопротивление ИЕЭ – реактивное.
Интенсивность обменных процессов оценивается реактивной мощностью:
.
2.3.3. Идеальный индуктивный элемент (ииэ)
Мгновенное значение напряжения на ИИЭ:
.
С учетом явления самоиндукции 2-й закон Кирхгофа для данной цепи:
.
Тогда ток, протекающий через ИИЭ:
– ток
отстает от напряжения на
.
Комплексное сопротивление ИИЭ:
,
где
[Ом] - индуктивное сопротивление.
- закон Ома в комплексной форме для ИИЭ.
Процессы в ИЕЭ и ИИЭ проходят в противофазе.
Интенсивность объемных процессов оценивается реактивной мощностью:
.
2.4. Комплексный (символический) метод расчета
Комплексный метод расчета применяется при анализе цепей с синусоидальными э.д.с., напряжениями и токами.
Сущность (математическая)комплексного метода анализа состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся интегродифференциальными уравнениями к алгебраическим уравнениям, составленными относительно комплексов тока и ЭДС.
При переходе дифференцирование мгновенного значения заменяют умножением jωна соответствующую комплексную величину, а интегрирование – делением комплексной величины наjω.
Основные законы электрических цепей в комплексной форме.
;
- закон Ома для участка цепи.
- закон Ома для
участка цепи, содержащего ЭДС.
- первый закон
Кирхгофа.
- второй закон
Кирхгофа.
Это позволяет в математическом описание параметров элементов схемы замещения (резистивных, индуктивных, емкостных) цепи переменного тока в комплексной форме вложить всю необходимую информацию о поведении этих элементов в цепи синусоидального тока.При этом каждый элемент заменяют на его комплексное изображение:
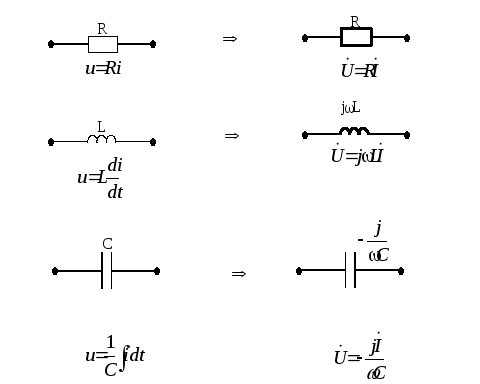
В результате получаем схему замещения в комплексной форме. К этой схеме применяют все известные методы расчета цепей постоянного тока.
Алгоритм комплексного метода
Составляют комплексную схему, заменяя мгновенные значения э.д.с., напряжений и токов источников тока их комплексными изображениями. Параметры ветвей схемы заменяют их комплексными сопротивлениями и проводимостями.
В полученной комплексной схеме произвольно выбирают направления комплексных токов в ветвях и обозначают их на схеме.
Составляют комплексные уравнения по выбранному методу расчета:
;
.
Решают уравнения относительно комплексного значения искомой величины:
.
При необходимости записывают мгновенное значение найденной комплексной величины:
.