1) , Где;

2) , где;

3) , где;

4) , где;

8. Градиент функции – это …

1) 2) 3)4)

9. В чем заключается геометрический смысл градиента?

1) указывает направление функции

2) указывает направление роста функции

3) Указывает направление наибыстрейшего роста функции

4) указывает направление, в котором функция постоянна

10. Необходимым условием экстремума функции двух переменных в точке является …

1) 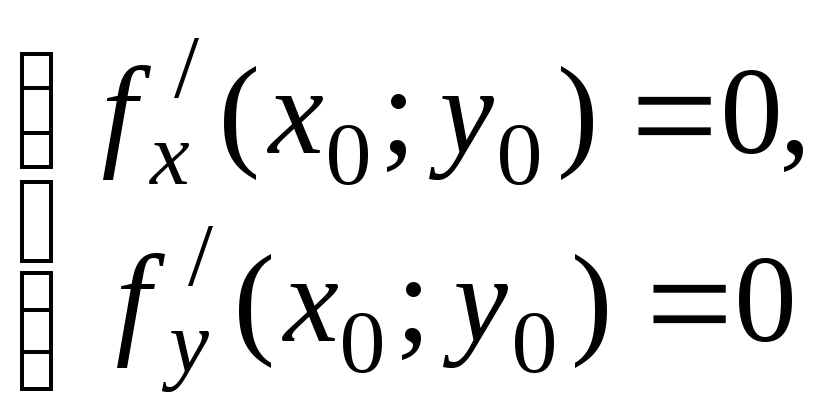2)

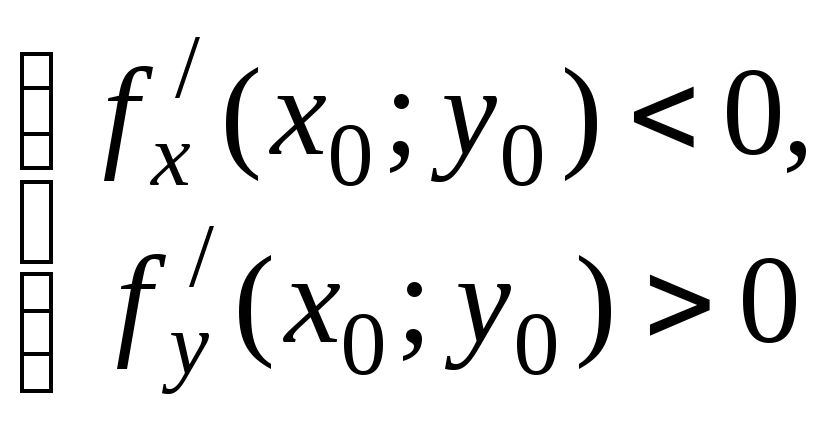3) 4)

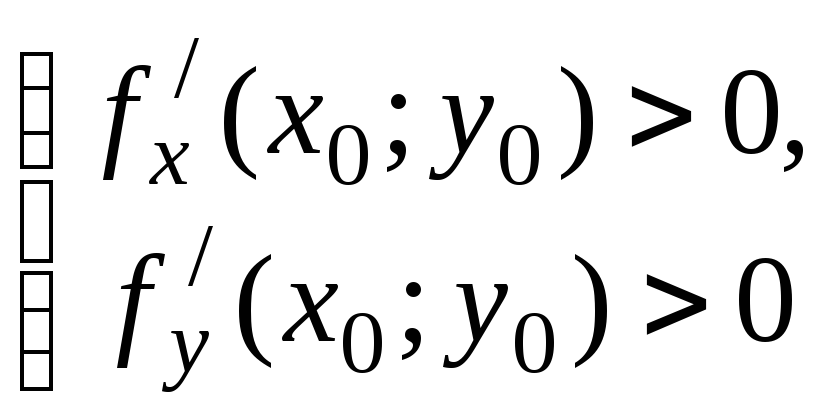
11. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

12. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

13. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

14. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

15. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

16. Пусть в стационарной точке и ее некоторой окрестности функцияимеет непрерывные частные производные до второго порядка включительно, причем;;;, тогда …

1) М₀ – точка минимума 2) М₀ – не является точкой экстремума

3) М₀ – точка максимума 4) нельзя определить

10