
Young D.C. - Computational chemistry (2001)(en)
.pdf262 33 RELATIVISTIC EFFECTS
couplings tend to be important for the heaviest actinides. For elements between these extremes, spin±orbit coupling is often included and other spin-coupling terms are sometimes included. The size of p orbitals is often relatively unchanged by relativistic e¨ects due to the mass defect and spin±orbit e¨ects canceling out.
Also arising from relativistic quantum mechanics is the fact that there should be both negative and positive energy states. One of these corresponds to electron energies and the other corresponds to the electron antiparticle, the positron.
33.2 EXTENSION OF NONRELATIVISTIC COMPUTATIONAL TECHNIQUES
The relativistic SchroÈdinger equation is very di½cult to solve because it requires that electrons be described by four component vectors, called spinnors. When this equation is used, numerical solution methods must be chosen.
The most common description of relativistic quantum mechanics for Fermion systems, such as molecules, is the Dirac equation. The Dirac equation is a oneelectron equation. In formulating this equation, the terms that arise are intrinsic electron spin, mass defect, spin couplings, and the Darwin term. The Darwin term can be viewed as the e¨ect of an electron making a high-frequency oscillation around its mean position.
The Dirac equation can be readily adapted to the description of one electron in the ®eld of the other electrons (Hartree±Fock theory). This is called a Dirac± Fock or Dirac±Hartree±Fock (DHF) calculation.
33.3CORE POTENTIALS
The most common way of including relativistic e¨ects in a calculation is by using relativisticly parameterized e¨ective core potentials (RECP). These core potentials are included in the calculation as an additional term in the Hamiltonian. Core potentials must be used with the valence basis set that was created for use with that particular core potential. Core potentials are created by ®tting a potential function to the electron density distribution from an accurate relativistic calculation for the atom. A calculation using core potentials does not have any relativistic terms, but the e¨ect of relativity on the core electrons is included.
The use of RECP's is often the method of choice for computations on heavy atoms. There are several reasons for this: The core potential replaces a large number of electrons, thus making the calculation run faster. It is the least computation-intensive way to include relativistic e¨ects in ab initio calculations. Furthermore, there are few semiempirical or molecular mechanics methods that are reliable for heavy atoms. Core potentials were discussed further in Chapter 10.
33.5 EFFECTS ON CHEMISTRY |
263 |
33.4EXPLICIT RELATIVISTIC CALCULATIONS
There are also ways to perform relativistic calculations explicitly. Many of these methods are plagued by numerical inconsistencies, which make them applicable only to a select set of chemical systems. At the expense of time-consuming numerical integrations, it is possible to do four component calculations. These calculations take about 100 times as much CPU time as nonrelativistic Hartree±Fock calculations. Such calculations are fairly rare in the literature.
Many researchers have performed calculations that include the two largemagnitude components of the spinnors. This provides a balance between high accuracy and making the calculation tractable. Such calculations are often done on atoms in order to obtain the wave function description used to create relativistic core potentials.
There are several ways to include relativity in ab initio calculations more e½ciently at the expense of a bit of accuracy. One popular technique is the Dirac±Hartree±Fock technique, which includes the one-electron relativistic terms. Another option is computing energy corrections to the nonrelativistic wave function without changing that wave function.
Relativistic density functional theory can be used for all electron calculations. Relativistic DFT can be formulated using the Pauli formula or the zero-order regular approximation (ZORA). ZORA calculations include only the zero-order term in a power series expansion of the Dirac equation. ZORA is generally regarded as the superior method. The Pauli method is known to be unreliable for very heavy elements, such as actinides.
Molecular mechanics and semiempirical calculations are all relativistic to the extent that they are parameterized from experimental data, which of course include relativistic e¨ects. There have been some relativistic versions of PM3, CNDO, INDO, and extended Huckel theory. These relativistic semiempirical calculations are usually parameterized from relativistic ab initio results.
33.5EFFECTS ON CHEMISTRY
As described above, relativistic e¨ects are responsible for shifts in the bond lengths of compounds, particularly those involving group 11 elements. This is called the gold maximum. For example, the Ag2 bond length predicted by nonrelativistic calculations will be in error by ÿ0.1 AÊ . The AuH deviation of ÿ0.2 AÊ and Au2 deviation of ÿ0.4 AÊ along with the Hg2 2‡ deviation of ÿ0.3 AÊ are among the largest known.
Relativistic e¨ects are cited for changes in energy levels, resulting in the yellow color of gold and the fact that mercury is a liquid. Relativistic e¨ects are also cited as being responsible for about 10% of lanthanide contraction. Many more speci®c examples of relativistic e¨ects are reviewed by PyykkoÈ (1988).
264 33 RELATIVISTIC EFFECTS
33.6RECOMMENDATIONS
The most di½cult part of relativistic calculations is that a large amount of CPU time is necessary. This makes the problem more di½cult because even nonrelativistic calculations on elements with many electrons are CPU-intensive. The following lists relativistic calculations in order of increasing reliability and thus increasing CPU time requirements:
1.Relativistic semiempirical calculations
2.Relativistic e¨ective core potentials
3.Dirac±Hartree±Fock
4.Relativistic density functional theory
5.Relativistic correlated calculations using the DHF Hamiltonian
6.Two-component calculations
7.Four-component calculations
BIBLIOGRAPHY
Introductory descriptions are
F.Jensen, Introduction to Computational Chemistry John Wiley & Sons, New York (1999).
M. Jacoby, Chem. & Eng. News March 23, 48 (1998).
C.B. Kellogg, An Introduction to Relativistic Electronic Structure Theory in Quantum Chemistry http://zopyros.ccqc.uga.edu/@kellogg/docs/rltvt/rltvt.html (1996).
I. N. Levine, Quantum Chemistry Fourth Edition Prentice Hall, Englewood Cli¨s (1991). W. H. E. Schwartz, Theoretical Models of Chemical Bonding Z. B. MaksicÏ, Ed.,
Springer-Verlag, Berlin (1990).
K. S. Pitzer, Acct. Chem. Res. 12, 271 (1979).
P. PyykkoÈ, J.-P. Desclaux, Acct. Chem. Res. 12, 276 (1979).
Review articles are
C. van Wullen, J. Comp. Chem. 20, 51 (1999).
K. Balasubramanian, Encycl. Comput. Chem. 4, 2471 (1998).
P. Schwerdtfeger, M. Seth, Encycl. Comput. Chem. 4, 2480 (1998). B. A. Hess, Encycl. Comput. Chem. 4, 2499 (1998).
J. Almlof, O. Gropen, Rev. Comput. Chem. 8, 203 (1996).
E.Engel, R. M. Dreizler, Density Functional Theory II Springer, Berlin (1996).
Y. Ishikawa, U. Kaldor, Computational Chemistry ± Reviews of Current Trends
J. Leszczynski, Ed., 1, World Scienti®c, Singapore (1996).
B.A. Hess, C. M. Marian, S. D. Peyerimho¨, Modern Electronic Structure Theory D. R. Yarkony, Ed., 152, World Scienti®c, Singapore (1995).
BIBLIOGRAPHY 265
K. Balasubramanian, Handbook on the Physics and Chemistry of Rare Earths K. A. Gschneidner, Jr., L. Eyring, Eds., 18, 29, Elsevier, Amsterdam (1994).
P. PyykkoÈ, Chem. Rev. 88, 563 (1988).
S. Wilson, Methods of Computational Chemistry Volume II Plenum, New York (1988). P. PyykkoÈ, Adv. Quantum Chem. 11, 353 (1978).
S.R. Langho¨, C. W. Kern, Modern Theoretical Chemistry 381, Plenum, New York (1977).
M. Bar®eld, R. J. Spear, S. Sternkell, Chem. Rev. 76, 593 (1976).
M. Bar®eld, B. Chakrabarti, Chem. Rev. 69, 757 (1969).
Books on relativistic quantum theory are
K. Balasubramanian, Relativistic E¨ects in Chemistry John Wiley & Sons, New York (1997).
R. Landau, Quantum Mechanics II John Wiley & Sons, New York, (1996). W. Greiner, Relativistic Quantum Mechanics Springer-Verlag, Berlin (1990).
A database of relativistic quantum mechanics references is at
http://www.csc.®/lul/rtam/
Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems. David C. Young Copyright ( 2001 John Wiley & Sons, Inc.
ISBNs: 0-471-33368-9 (Hardback); 0-471-22065-5 (Electronic)
34 Band Structures
In molecules, the possible electronic energies are discrete, quantized energy levels. As molecules become larger, these energy levels move closer together. In a crystal, the energy levels have merged together so closely that they are continuous bands of available energies for all practical purposes. Thus, the electronic structure of a crystal is described by its band structure.
34.1MATHEMATICAL DESCRIPTION OF ENERGY BANDS
The electronic structure of an in®nite crystal is de®ned by a band structure plot, which gives the energies of electron orbitals for each point in k-space, called the Brillouin zone. This corresponds to the result of an angle-resolved photo electron spectroscopy experiment.
k-space is not a physical space. It is a description of the bonding nature of orbitals. In an in®nitely long string of atoms, the phases of orbitals might be anywhere from all bonding to all antibonding (these extremes are labeled as k ˆ 0 and k ˆ p=a). Somewhere in between are combinations with three atoms in a row oriented for bonding, followed by an antibonding one or any other such combination. As k-space is de®ned, k ˆ 0 corresponds to complete bonding symmetry for some orbitals and complete antibonding for others, depending on the symmetry of the atomic orbitals.
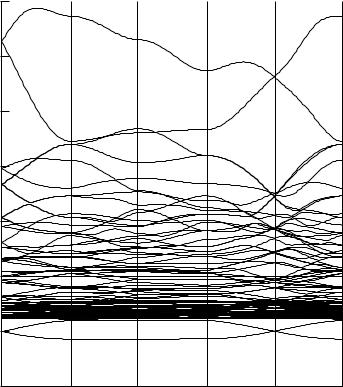
k-space will have three dimensions …kx; ky; kz† for three-dimensional crystals. Certain points in k-space are given names. The designator G refers to the point where k ˆ 0 in all dimensions. M is the point with k ˆ p=a in all directions. X, Y, K, and A are points with k ˆ 0 in some directions and k ˆ p=a in others, depending on the symmetry of the crystal. The typical band structure plot, called a spaghetti plot, maps the orbital energies along the paths between these points, as shown in Figure 34.1. These designations are discussed in more detail in the literature cited in the bibliography.
As orbitals spread into bands, orbitals oriented for s or s bonds spread into the widest bands. p orbitals form narrower bands and d bonding orbitals form the narrowest bands.
34.2COMPUTING BAND GAPS
In some cases, researchers only need to know the band gap for a crystal. Once a complete band structure has been computed, it is, of course, simple to ®nd the
266
34.2 COMPUTING BAND GAPS 267
|
100 |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
60 |
|
|
|
|
|
Energy (eV) |
40 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
-40 |
Γ |
X |
M |
R |
Γ |
|
Z |
FIGURE 34.1 Band-structure plot for CoNb4Si.
band gap by inspection. However, computing the entire band structure could involve an extensive amount of work to obtain a lot of unneeded information. There are ways of estimating the band gap, although these are not completely reliable.
Simply doing electronic structure computations at the M, K, X, and G points in the Brillouin zone is not necessarily su½cient to yield a band gap. This is because the minimum and maximum energies reached by any given energy band sometimes fall between these points. Such limited calculations are sometimes done when the computational method is very CPU-intensive. For example, this type of spot check might be done at a high level of theory to determine whether complete calculations are necessary at that level.
Some researchers use molecule computations to estimate the band gap from the HOMO±LUMO energy separation. This energy separation becomes smaller as the molecule grows larger. Thus, it is possible to perform quantum mechanical calculations on several molecules of increasing size and then extrapolate the energy gap to predict a band gap for the in®nite system. This can be useful for polymers, which are often not crystalline. One-dimensional band structures are
268 34 BAND STRUCTURES
also used for such systems, thus assuming crystallinity or at least a high degree of order.
34.3COMPUTING BAND STRUCTURES
Since ab initio and semiempirical calculations yield orbital energies, they can be applied to band-structure calculations. However, if it is time-consuming to calculate the energy for a molecule, it is even more time-consuming to calculate energies for a list of points in the Brillouin zone. Since these calculations are so computationally intensive, extended HuÈckel has been the method of choice unless more accurate results are needed. In the realm of band-structure calculations, extended HuÈckel is sometimes called the tight binding approximation. In recent years, there has been an increasing tendency to use ab initio or DFT methods.
Like molecular calculations, an ab initio method requires both a set of basis functions and a means for computing the energy. The choice of basis sets for band structure calculations is somewhat di¨erent than for molecular calculations. Large basis sets with di¨use functions can contain contractions having a large overlap, with their image in the adjacent unit cell. When this happens, it creates a linear dependency that prevents the self-consistent equations from being solved. Most often, smallto medium-size basis sets are used to avoid this problem. The linear combination of atomic orbitals (LCAO) scheme used for molecular calculations can be applied to crystal calculations, but it is not the only option. Actually, the basis functions centered on atoms are formed into Bloch functions, which obey the translational symmetry of the system, although the term LCAO is still used.
Another basis technique that is popular for modeling crystals is the use of plane wave basis functions. Plane waves were proposed because they re¯ect the in®nite symmetry of a crystal. There have been several di¨erent plane wave techniques proposed. The earliest plane wave calculations assumed the SchroÈdinger equation was spherically symmetric in a region around each atom (dubbed a mu½n tin potential), but su¨ered from an inability to conserve charge. These mu½n tin calculations gave reasonable results for ionic crystals. They are no longer performed since algorithms and computer hardware improvements make more accurate and reliable calculations feasible. A technique still used is the augmented plane wave (APW) technique, which is a cellular calculation over the Vigner±Seitz cell. There are many other basis function methods that are used for certain types of problems.
Band structure calculations have been done for very complicated systems; however, most of software is not yet automated enough or su½ciently fast that anyone performs band structures casually. Setting up the input for a band structure calculation can be more complex than for most molecular programs. The molecular geometry is usually input in fractional coordinates. The unit cell lattice vectors and crystallographic angles must also be provided. It may be nec-
34.4 DESCRIBING THE ELECTRONIC STRUCTURE OF CRYSTALS |
269 |
essary to provide a list of k points and their degeneracies. It is safest to check the convergence of any input option a¨ecting the calculation accuracy. Manuals accompanying the software may give some suggested values. Researchers wishing to complete band structure calculations should expect to put a lot of time into their e¨orts particularly during the learning stage for the software to be used.
As mentioned above, the preferred computational methods for modeling crystals have changed over the years. Below is a list of basis function schemes, with the most often used appearing ®rst:
1.Linear combination of atomic orbitals (LCAO)
2.Augmented plane wave method (APW)
3.Green's function method of Korringa, Kohn, and Rostoker (sometimes denoted KKR)
4.Orthogonalized plane wave (OPW)
5.Pseudopotential method
6.Various approximate or empirical methods
Any orbital-based scheme can be used for crystal-structure calculations. The trend is toward more accurate methods. Some APW and Green's function methods use empirical parameters, thus edging them toward a semiempirical classi®cation. In order of preference, the commonly used methods are:
1.Self-consistent ab initio or DFT methods
2.Semiempirical methods
3.Methods using an ad hoc or model potential
34.4DESCRIBING THE ELECTRONIC STRUCTURE OF CRYSTALS
The population analysis techniques used for molecular calculations are not directly applicable to band structure calculations. A series of techniques for analyzing the band structure have been introduced. These are generally presented as graphical plots. The data for these plots come from a series of calculations at various points in k-space. Very good plots can be obtained by calculating a very large number of points. In order to reduce computer time, a more widely spaced set of points can be generated; then the plots are smoothed by some kind of interpolation algorithm. It is always prudent to perform several calculations with points increasingly close together to see if the plot changes signi®cantly.
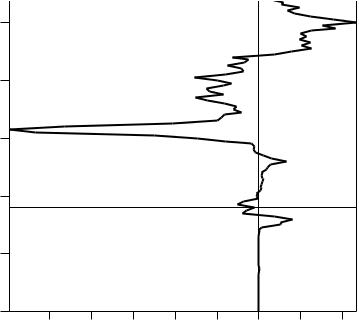
One important question is how many orbitals are available at any given energy level. This is shown using a density of states (DOS) diagram as in Figure 34.2. It is typical to include the Fermi level as denoted by the dotted line in this ®gure. A material with a half-®lled energy band is a conductor, but it may be a

270
(eV) Energy
34 BAND STRUCTURES
20
10
0
10
20
30
0 |
2 |
4 |
6 |
8 |
10 |
12 |
DOS
FIGURE 34.2 Density of states plot for CoNb4Si.
very poor conductor if there are very few un®lled orbitals available. In some cases, the contributions of a particular orbital to the DOS are plotted on the same graph as a shaded region or dotted line.
Another question is whether the ®lled orbitals are of a bonding or antibonding character. This is displayed on a crystal orbital overlap population (COOP) plot as shown in Figure 34.3. Typically, the positive bonding region is plotted to the right of the zero line.
The Fermi energy is the energy of the highest-energy ®lled orbital, analogous to a HOMO energy. If the orbital is half-®lled, its energy will be found at a collection of points in k-space, called the Fermi surface.
34.5COMPUTING CRYSTAL PROPERTIES
There has not been as much progress computing the properties of crystals as for molecular calculations. One property that is often computed is the bulk modulus. It is an indication of the hardness of the material.
It may be desirable to predict which crystal structure is most stable in order to predict the products formed under thermodynamic conditions. This is a very di½cult task. As of yet, no completely automated way to try all possible crystal structures formed from a particular collection of elements (analogous to a molecular conformation search) has been devised. Even if such an e¨ort were attempted, the amount of computer power necessary would be enormous. Such studies usually test a collection of likely structures, which is by no means infal-
Energy (eV)
BIBLIOGRAPHY 271
20
10
0
10
20
30
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
0.1 |
0.2 |
COOP
FIGURE 34.3 Crystal orbital overlap plot for CoNb4Si.
lible. Energy minimizations can be performed, provided that the starting structure has the correct symmetry.
34.6DEFECT CALCULATIONS
Sometimes, the system of interest is not the in®nite crystal, but an anomaly in the crystal, such as an extra atom adsorbed in the crystal. In this case, the in®nite symmetry of the crystal is not rigorously correct. The most widely used means for modeling defects is the Mott±Littleton defect method. It is a means for performing an energy minimization in a localized region of the lattice. The method incorporates a continuum description of the polarization for the remainder of the crystal.
BIBLIOGRAPHY
Text books describing band structures are
P. Y. Yu, M. Cardone, Fundamentals of Semicondutors Springer-Verlag, Berlin (1996).
