Ersoy O.K. Diffraction, Fourier optics, and imaging (Wiley, 2006)(ISBN 0471238163)(427s) PEo

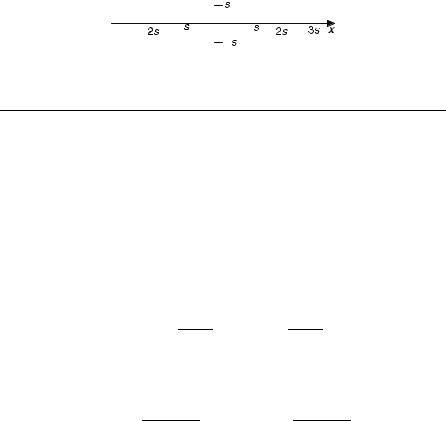
Figure 10.8. The aperture function for Example 10.9.

EXAMPLE 10.9 An exit aperture function consists of two open squares as shown in Figure 10.8.

Determine

(a)the coherent transfer function

(b)the coherent cutoff frequencies

(c)the amplitude impulse response

(d)the optical transfer function

Solution: (a) The coherent transfer function is the same as the scaled aperture function. Mathematically, the aperture function can be written as

(c) The amplitude impulse response hðx; yÞ is the inverse Fourier transform of Hð fx; fyÞ. Let a be equal to ld0s. hðx; yÞ is computed as

(d) The total area A under Hð fx; fyÞ equals 8s2. The OTF is given by

ðð1

HI ð fx; fyÞ ¼ Hð fx0; fy0ÞH ð fx0 fx; fy0 fyÞd fx0d fy0

1

A

The computation of the above integral is not trivial and can be best done by the computer.

10.9 COMPUTER COMPUTATION OF THE OPTICAL TRANSFER FUNCTION

The easiest way to compute the discretized OTF is by using the FFT. For this purpose, both hðx; yÞ; Hð fx; fyÞ and HI ð fx; fyÞ, have to be discretized. The discretized coordinates can be written as follows:

hðn1; n2Þ, Hðk1; k2Þ, and HI ðk1; k2Þ, respectively. The size of the matrices involved are assumed to be N1, by N2. In order to use the FFT, the following must be satisfied:

Hðk1; k2Þ equals Pð ld0 fxk1; ld0 fyk2Þ. N1 and N2 should be chosen such that the pupil function is sufficiently represented. For example, the nonzero portion of the pupil function must be completely covered. In order to minimize the effect of periodicity imposed by the FFT, N1 and N2 should be at least twice as large the minimum values dictated by the nonzero portion of the pupil function.

Once N1 and N2 are properly chosen, Hðk1; k2Þ is arranged as discussed in Section 4.4 so that k1 and k2 satisfy 0 k1 < N1 and 0 k2 < N2 respectively.

HI ðk1; k2Þ is approximately given by

The numerator above is the 2-D DFT of jh0ðn1; n2Þj2. HI ðk1; k2Þ above is actually shifted to positive frequencies because of the underlying periodicity. It should be shifted down again to include negative frequencies.

In summary, Hðk1; k2Þ is determined by using the pupil function. h0ðn1; n2Þ is obtained by the inverse DFT of Hðk1; k2Þ according to Eq. (10.9-8). HI ðk1; k2Þ is given by the DFT of jh0ðn1; n2Þj2 normalized by the area under jHðk1; k2Þj2.

Note that fx and fy should be chosen small enough so that h0ðn1; n2Þ is not aliased when computed by using Eq. (10.9-8). Once fx and fy are chosen, N1 and N2 are determined by considering the pupil function as discussed above.

10.9.1Practical Considerations

In studies of the OTF and MTF, ld0 is often chosen to be equal to 1, and the negative signs in the pupil function are neglected so that Hðfx; fyÞ is simply written as Pð fx; fyÞ. Normalization by the area of the pupil function may also be neglected.

Another way to generate OTF is by autocorrelating the pupil function with itself.

10.10ABERRATIONS

A diffraction-limited system means the wave of interest is perfect at the exit pupil, and the only imperfection is the finite aperture size. The wave of interest is typically a spherical wave. Aberrations are departures of the ideal wavefront within the exit pupil from its ideal form. They are typically phase errors.

In order to include aberrations, the exit pupil function can be modified as

where Pðx; yÞ is the exit pupil function without aberrations, and fAðx; yÞ is the phase error due to aberrations.

The theory of coherent and incoherent imaging developed in the previous sections is still applicable with the replacement of Pðx; yÞ by PAðx; yÞ. For example, the amplitude transfer function becomes

Note that Að fx; fyÞ is to be computed in the area of overlap of the two pupil functions shifted with respect to each other. The ordinary pupil function in this area