
Ersoy O.K. Diffraction, Fourier optics, and imaging (Wiley, 2006)(ISBN 0471238163)(427s) PEo
.pdf
78 |
FRESNEL AND FRAUNHOFER APPROXIMATIONS |
wavelengths travel in different directions. The peak intensity at each wavelength depends on the number of slits in the grating.
The transmission function of a grating is defined by
t |
ð |
x; y |
Þ ¼ |
Uðx; y; 0þÞ |
ð |
5:6-2 |
Þ |
|
|
Uðx; y; 0 Þ |
|
where Uðx; y; 0 Þ and Uðx; y; 0þÞ are the wave functions immediately before and after the grating, respectively. If the grating is of reflection type, the transmission function becomes the reflection function.
t(x,y) is, in general, complex. If arg(t(x,y)) equals zero, the grating modifies the amplitude only. If jtðx; yÞj equals a constant, the grating modifies the phase only.
Gratings are sometimes manufactured to work with the reflected light, for example, by metalizing the surface of the grating. Then, the transmission function becomes the reflection function.
The phase of the incident wave can be modulated by periodically varying the thickness or the refractive index of a transparent plate. Reflecting diffraction gratings can be generated by fabricating periodically ruled thin films of aluminum evaporated on a glass substrate.
5.7 FRAUNHOFER DIFFRACTION BY A SINUSOIDAL AMPLITUDE GRATING
Assuming a plane wave incident perpendicularly on the grating with unity amplitude, the transmission function is the same as U(x,y,0) given by
1 |
|
m |
x |
|
y |
|
||
Uðx; y; 0Þ ¼ |
|
þ |
|
cosð2pf0xÞ rect |
|
rect |
|
ð5:7-3Þ |
2 |
2 |
D |
D |
|||||
where the diffraction grating is assumed to be limited to a square aperture of width D. U(x,y,0) can be written as
Uðx; y; 0Þ ¼ f ðx; yÞgðx; yÞ |
ð5:7-4Þ |
where
|
1 |
|
m |
|
|
|
|||
f ðx; yÞ ¼ |
|
þ |
|
|
cosð2pf0xÞ |
ð5:7-5Þ |
|||
2 |
2 |
||||||||
|
|
|
|
x |
y |
|
|||
gðx; yÞ ¼ rect |
|
|
rect |
|
|
ð5:7-6Þ |
|||
|
D |
D |
|||||||

FRESNEL DIFFRACTION BY A SINUSOIDAL AMPLITUDE GRATING |
79 |
The FTs of f(x,y) and g(x,y) are given by
Fðfx; fyÞ ¼ 1 dðfx; fyÞ þ m ½dðfx þ f0; fyÞ þ dðfx f0; fyÞ&
2 4
Gðfx; fyÞ ¼ D2 sin cðDfxÞ sin cðDfyÞ
The FT of U(x,y,0) is the convolution of Fðfx; fyÞ with Gðfx; fyÞ:
Uðx; y; 0Þ $ Fðfx; fyÞ Gðfx; fyÞ
where |
|
|
Fðfx; fyÞ Gðfx; fyÞ |
2 ðsin c½Dðfx þ f0Þ& þ sin c½Dðfx f0Þ&Þ |
|
¼ 2 sin cðDfyÞnhsin cðDfxÞ þ |
||
|
D2 |
m |
Then, the wave field at z is given by
ð5:7-7Þ
ð5:7-8Þ
ð5:7-9Þ
io
ð5:7-10Þ
|
ejkz |
|
k 2 |
2 |
ÞFð fx; fyÞ Gð fx; fyÞ |
|
|
Uðx0; y0; zÞ ¼ |
|
ej |
|
ðx0 |
þy0 |
ð5:7-11Þ |
|
|
2z |
||||||
jlz |
|||||||
where fx ¼ x0=lz and fy ¼ y0=lz.
5.8 FRESNEL DIFFRACTION BY A SINUSOIDAL AMPLITUDE GRATING
In order to compute Fresnel diffraction by a sinusoidal amplitude grating, we can use the convolution form of the diffraction integral given by Eq. (5.2-8). The transfer function of the system is rewritten here as
Hðfx; fyÞ ¼ ejkze jplzðfx2þfy2Þ |
ð5:8-1Þ |
where ejkz can be suppressed as it is a constant phase factor.
The Fourier transform of the transmittance function is given by Eq. (5.7-9). In order to simplify the computations, we will assume that the diffraction grating aperture is large so that the Fourier transform of the transmittance function of the grating can be approximated by Eq. (5.7-7). Then, the frequencies that contribute are given by
ðfx; fyÞ ¼ ð0; 0Þ; ð f0; 0Þ; ðf0; 0Þ
The propagated wave has the following Fourier transform:
|
1 |
|
m |
2 |
2 |
|
Uðx0; y0; zÞ $ |
|
dðfx; fyÞ þ |
|
½e jplzf0 |
dðfx f0; fyÞ þ e jplzf0 |
dðfx þ f0; fyÞ& ð5:8-2Þ |
2 |
4 |

80 |
FRESNEL AND FRAUNHOFER APPROXIMATIONS |
The inverse Fourier transform yields
Uðx0; y0; zÞ ¼ 12 þ m4 e jplzf02 ½ej2pf0x0 þ e j2pf0x0 &
ð5:8-3Þ
¼ 12 ½1 þ m e jplzf 02 cosð2pf0x0Þ&
The intensity of the wave is given by
Iðx0; y0; zÞ ¼ |
1 |
1 |
þ 2mcos plzf02 cosð2pf0x0Þ þ m2 cos2ð2pf0x0Þ |
ð5:8-4Þ |
4 |
EXAMPLE 5.11 Determine the intensity of the diffraction pattern at a distance z that satisfies
2n
z ¼ n integers
lf02
Solution: Iðx0; y0; zÞ is given by
Iðx0; y0; zÞ ¼ 14 ½1 þ mcosð2pf0x0Þ&2
This is the image of the grating. Such images are called Talbot images or selfimages.
EXAMPLE 5.12 Repeat the previous example if
z |
¼ |
|
ð2n þ 1Þ |
n integer |
|
lf02 |
|||||
|
|
|
Solution: Iðx0; y0; zÞ is given by
Iðx0; y0; zÞ ¼ 14 ½1 mcosð2pf0x0Þ&2
This is the image of the grating with a 180 spatial phase shift, referred to as contrast reversal. Such images are also called Talbot images.

FRAUNHOFER DIFFRACTION WITH A SINUSOIDAL PHASE GRATING |
81 |
EXAMPLE 5.13 Repeat the previous example if
z |
¼ |
2n 1 |
|
n integer |
|||
|
|
2lf02 |
|
|
|
|
|
Solution: Iðx0; y0; zÞ is given by |
|
|
|
|
|
|
|
|
|
1 |
|
m2 |
|
m2 |
|
Iðx0; y0; zÞ ¼ |
|
1 þ |
|
þ |
|
cosð4pf0x0Þ |
|
4 |
2 |
2 |
|||||
This is the image of the grating at twice the frequency, namely, 2f0. Such images are called Talbot subimages.
5.9 FRAUNHOFER DIFFRACTION WITH A SINUSOIDAL PHASE GRATING
As with the sinusoidal amplitude grating, with an incident plane wave on the grating, the transmission function for a sinusodial phase grating is given by
m |
x |
y |
|
||||||
Uðx; y; 0Þ ¼ ej2 sinð2pf0xÞrect |
|
rect |
|
|
ð5:9-1Þ |
||||
D |
D |
||||||||
U(x,y,0) can be written as |
|
|
|
|
|
|
|
||
Uðx; y; 0Þ ¼ f ðx; yÞgðx; yÞ |
|
|
ð5:9-2Þ |
||||||
where |
|
|
|
|
|
|
|
||
f ðx; yÞ ¼ ejm2 sinð2pf0xÞ |
|
|
|
|
|
|
ð5:9-3Þ |
||
|
x |
|
|
y |
|
|
|
||
gðx; yÞ ¼ rect |
|
rect |
|
|
|
|
ð5:9-4Þ |
||
D |
D |
|
|
||||||
The analysis can be simplified by use of the following identity:
|
m |
X |
m |
|
|
|
1 |
ej2pf0kx |
|
||
ej |
2 sinð2pf0xÞ ¼ k¼ 1 Jk |
2 |
ð5:9-5Þ |
||
where Jkð Þ is the Bessel function of the first kind of order k. Using the above identity, the FT of f(x,y) is given by
X |
m |
|
|
1 |
dð fx kf0; fyÞ |
|
|
Fðfx; fyÞ ¼ k¼ 1 Jk |
2 |
ð5:9-6Þ |
82 FRESNEL AND FRAUNHOFER APPROXIMATIONS
The FT of U(x,y,0) is given by |
|
|
|
|
|
|
|
|
Uðx; y; 0Þ $ Fðfx; fyÞ Gðfx; fyÞ |
ð5:9-7Þ |
|||||||
where |
|
|
|
|
|
|
|
|
X |
|
|
|
m |
|
|
||
|
1 |
|
|
|
sinc½Dðfx kf0Þ& sincðDfyÞ |
|
||
Fðfx1; fyÞ Gðfx; fyÞ ¼ D2 k¼ 1 Jk |
2 |
ð5:9-8Þ |
||||||
Then, |
|
|
|
|
|
|
|
|
|
|
ejkz |
|
k |
2 |
2 |
|
|
Uðx0; y0; zÞ ¼ |
|
|
ej |
2z |
ðx0þy0ÞFð fx; fyÞ Gð fx; fyÞ |
ð5:9-9Þ |
||
|
jlz |
|||||||
It is observed that sinusoidal amplitude grating in Section 5.7 has three orders of energy concentration due to three sin c functions, which do not significantly overlap if the grating frequency is much greater than 2/D. In contrast, the sinusoidal phase grating has many orders of energy concentration. Whereas the central order is dominant in the amplitude grating, the central order may vanish in the phase grating when J0ðm=2Þ equals 0.
5.10DIFFRACTION GRATINGS MADE OF SLITS
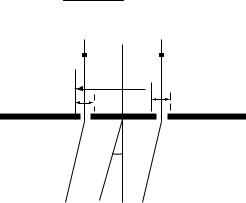
Sometimes diffraction gratings are made of slits. A two-slit example is shown in Figure 5.9, where b is the slit width, and f is the diffraction angle as shown in this figure.
The intensity of the wave field coming from the grating in the Fraunhofer region can be shown to be
I |
|
2I |
|
|
sinðkbf=2Þ |
|
2 |
1 |
cos |
k |
|
kd |
|
|
5:10-1 |
|
ðfÞ ¼ |
|
|
þ |
fÞ& |
ð |
Þ |
||||||||||
|
kbf=2 |
|
||||||||||||||
|
|
0 |
|
½ þ |
ð |
|
|
|
d
b 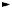 b
b
φ
Figure 5.9. A two-slit diffraction grating.

DIFFRACTION GRATINGS MADE OF SLITS |
83 |
where is the difference of the optical path lengths between the rays of two adjacent slits and I0 is the initial intensity of the beam.
When there are N parallel slits, the intensity in the Fraunhofer region can be shown to be
I |
|
2I |
|
|
sinðkbf=2Þ |
2 |
sinðNkdf=2Þ |
|
2 |
|
5:10-2 |
|
ðfÞ ¼ |
|
|
ð |
Þ |
||||||||
|
kbf=2 |
|
|
|||||||||
|
|
0 |
sinðkdf=2Þ |
|
|
|||||||
The second factor above equals N cosðpNmÞ= cosðpmÞ when the grating equation d sin f ¼ ml is satisfied.

6
Inverse Diffraction
6.1INTRODUCTION
Inverse diffraction involves recovery of the image of an object whose diffraction pattern is measured, for example, on a plane. In the case of the Fresnel and Fraunhofer approximations, the inversion is straightforward. In the very near field, the angular spectrum representation can be used, but then there are some technical issues that need to be addressed.
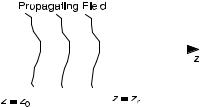
The geometry to be used in the following sections is shown in Figure 6.1. The observation plane and the measurement plane are assumed to be at z ¼ z0 and z ¼ zr, respectively. Previously, zr was chosen equal to 0. The distance between the two planes is denoted by z0r. The medium is assumed to be homogeneous. The problem is to determine the field at z ¼ z0, assuming it is known at z ¼ zr.
Like all inverse problems, the inverse diffraction problem is actually difficult if evanescent waves are to be incorporated into the solution [Vesperinas, 1991]. Then, the inverse diffraction problem involves a singular kernel [Shewell, Wolf, 1968]. When the evanescent waves are avoided as discussed in the succeeding sections, the problem is well behaved.
This chapter consists of four sections. Section 2 is on inversion of the Fresnel and Fraunhofer approximations. Section 6.3 describes the inversion of the angular spectrum representation. Section 6.4 discusses further analysis of the results of Section 6.3.
6.2 INVERSION OF THE FRESNEL AND FRAUNHOFER REPRESENTATIONS
The Fresnel diffraction is governed by Eq. (5.2-13). As the integral is a Fourier transform, its inversion is given by
|
je jkz0r |
|
k |
2 |
2 |
|
1 1 |
|
k |
2 |
2 |
|
2p |
|
Uðx; y; zrÞ ¼ |
|
e j |
|
ðx |
þy |
Þ |
ð ð |
Uðx0; y0; z0Þe j |
|
ðx0 |
þy0 |
Þej |
|
ðx0xþy0yÞdx0dy0 |
|
2z0r |
2z0r |
lz0r |
|||||||||||
lz |
||||||||||||||
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
ð6:2-1Þ
Diffraction, Fourier Optics and Imaging, by Okan K. Ersoy
Copyright # 2007 John Wiley & Sons, Inc.
84
INVERSION OF THE ANGULAR SPECTRUM REPRESENTATION |
85 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 6.1. Geometry for inverse diffraction.
where zr and z0 are the input and output z variables, and z0r ¼ z0 zr.
The Fraunhofer diffraction is governed by Eq. (5.4-2). Its inversion is given by
|
je jkz0r |
1 1 |
|
k |
2 |
2 |
|
2p |
|
Uðx; y; zrÞ ¼ |
|
ð ð |
Uðx0; y0; z0Þe j |
|
ðx0 |
þy0 |
Þe j |
|
ðx0xþy0yÞdx0dy0 ð6:2-2Þ |
|
2z0r |
lz0r |
|||||||
lz0r |
|||||||||
|
|
1 1 |
|
|
|
|
|
|
|
6.3 INVERSION OF THE ANGULAR SPECTRUM REPRESENTATION
Below the method is first discussed in 2-D. Then, it is generalized to 3-D. Equation (4.3-12) in 2-D can be written as
|
1 |
|
|
Uðx0; z0Þ ¼ |
1 |
ð6:3-1Þ |
|
ð |
Aðfx; zrÞejz0r pk2 4p2fx2 e j2pfxx0 dfx |
As this is a Fourier integral, recovery of Aðfx; zrÞ involves the computation of the Fourier transform of Uðx0; z0Þ:
|
1 |
Uðx0; z0Þe j2pfxx0 dx0 |
|
1 |
ð6:3-2Þ |
||
Aðfx; zrÞ ¼ e jz0r pk2 4p2fx2 |
ð |
Uðx; zrÞ is the inverse Fourier transform of Aðfx; zrÞ:
Uðx; zrÞ ¼ |
1 |
2 1 |
Uðx0; z0 |
Þe j2pfxx0 dx03e jz0r pk2 |
4p2fx2 e j2pfxxdfx |
ð6:3-3Þ |
|
ð |
ð |
|
|
|
|
|
1 |
41 |
|
5 |
|
|
With F[.] and F 1[.] indicating the forward and inverse Fourier transforms, Eq. (6.3-3) can be expressed as
h |
pi |
ð6:3-4Þ |
Uðx; zrÞ ¼ F 1 F½Uðx0; z0Þ&e jz0r |
k2 4p2fx2 |
86 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INVERSE DIFFRACTION |
|||
In 3-D, the corresponding equation is given by |
|
|
|
|
||||||||||||||||
U |
ð |
x |
; ; |
rÞ ¼ |
F |
|
h |
½ |
U |
ð |
x |
0; |
y |
0; |
z |
0Þ& |
i |
ð : |
3-5 |
Þ |
|
y z |
|
|
1 |
F |
|
|
|
e jz0r pk2 4p2ðfx2þfy2Þ |
6 |
|
|||||||||
Note that zr can be varied above to reconstruct the wave field at different depths. In this way, a 3-D wave field reconstruction is obtained.
If measurements are made with nonmonochromatic waves, resulting in a wave field Uðx0; y0; z0; tÞ, where t indicates the time dependence, a single time frequency component Uðx0; y0; z0; f Þ can be chosen by computing
|
1 |
|
|
|
|
|
Uðx0; y0; z0; f Þ ¼ |
ð |
Uðx0; y0; z0; tÞe j2pftdt |
ð6:3-6Þ |
|||
1 |
|
|
|
|
||
Then, the equations discussed above can be used with k given by |
|
|||||
k ¼ |
|
2p |
¼ 2p |
f |
ð6:3-7Þ |
|
|
l |
v |
|
|||
where v is the phase velocity. The technique discussed above was used with ultrasonic and seismic image reconstruction [Boyer, 1971; Boyer et al., 1970; Ljunggren, 1980]. It is especially useful when z0r is small so that other approximations to the diffraction integral, such as Fresnel and Fraunhofer approximations discussed in Chapter 5, cannot be used.
6.4 ANALYSIS
Interchanging orders of integration in Eq. (6.4-3) results in
1ð
Uðx; zrÞ ¼ Uðx0; z0ÞBðx; x0Þdx0 |
ð6:4-1Þ |
1
where
p
Bðx; x0Þ ¼ |
e jz0r k2 4p2fx2 e j2pfxðx x0Þdfx |
ð6:4-2Þ |

ANALYSIS |
87 |
integration are restricted such that k > 2pfx [Lalor, 1968]. Then, fx is restricted to the range
1 |
ð6:4-3Þ |
jfxj l |
Suppose that the exact wave field at z ¼ zr is T(x,zr). How does U(x,zr) as computed above compare to T(x,zr)? In order to answer this question, we can first determine Uðx0; z0Þ in terms of T(x,zr) by forward diffraction. This is given by
|
|
Uðx0; z0Þ ¼ |
|
ð |
|
|
ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð6:4-4Þ |
||||
|
|
|
M 2 |
1 Tðx; zrÞe j2pfxxdx3ejz0r pk2 4p2fx2 ej2pfxx0 dfx |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||
where jfxj M is used. The upper bound for M is 1/l. |
|
|
|
|
|
|||||||||||||||||||||
|
Substituting this result in Eq. (6.4-3) and allowing fx to the range fx Q results in |
|||||||||||||||||||||||||
|
|
Uðx; zrÞ ¼ |
ð |
|
|
ð |
2 |
ð |
|
|
|
|
|
|
|
|
|
9 |
|
|
||||||
|
|
Q |
|
8 M |
1 Tðx; zrÞe j2pfx0xdx3ejz0r pk2 4p2fx02 ej2pfxx0 dfx0 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
Q |
< |
|
M |
|
|
|
|
|
|
|
|
5 |
|
|
= |
|
|
|||
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
x |
|
|
|
|
; |
|
|
||||
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
e jz0r pk2 4p2fx2 ej2pfxxdf |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Interchanging orders of integration, this can be written as [Van Rooy, 1971] |
|||||||||||||||||||||||||
|
|
|
ð |
ð |
|
dfx0e j2pfx0xejz0r pk2 |
4p2fx0 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
Uðx; zrÞ ¼ 1 |
2 M |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
4 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 Q |
dfxe j2pfxxe jz0r pk2 4p2fx2 |
|
1 |
dx0ej2px0ðfx0 fxÞ 13T |
|
x; zr |
dx |
||||||||||||||
|
|
|
|
|
|
|
|
ð |
|
|
|
|
|
|
|
2 |
ð |
3 |
|
ð |
|
Þ |
|
|||
|
|
|
|
|
B Q |
|
|
|
|
|
|
4 |
1 |
C7 |
|
|
|
|
|
|||||||
|
|
|
|
|
@ |
|
|
|
|
|
|
|
|
|
|
|
|
5A5 |
|
|
|
|
|
|||
As |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dðfx fx0Þ ¼ |
ð |
|
ej2pxðfx0 fxÞdx |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Eq. (6.4-4) becomes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U x; zr |
1 2 Me j2pfx0x0 ejz0r pk2 4p2fx02 dfx0 Qd fx fx0 ej2pfxxe jz0r pk2 4p2fx2 dfx3T x; zr dx |
|||||||||||||||||||||||||
ð |
|
16 M |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
7 |
ð |
|
Þ |
||||||
|
Þ ¼ð |
ð |
|
|
|
|
|
|
|
|
|
|
ð |
ð Þ |
|
|
5 |
|
||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
