Mueller M.R. - Fundamentals of Quantum Chemistry[c] Molecular Spectroscopy and Modern Electronic Structure Computations (Kluwer, 2001)
.pdf
6 |
Chapter 1 |
Taking the derivative of the Hamiltonian (Equation 1-7) with respect to position and applying Equation 1-5 yields:
Taking the derivative of the Hamiltonian (Equation 1-7) with respect to momentum and applying Equation 1-6 yields:
The second differential equation yields a trivial result:
however, the first differential equation can be used to determine the trajectory of the mass m. The time derivative of momentum is equivalent to the force, or mass times acceleration.
Classical Mechanics |
7 |
or
The solution to this differential equation is well known. One solution is given below.
Another mathematically equivalent solution can be found by utilizing the following Euler identities 
and
This results in the following mathematically equivalent trajectory as in Equation 1-9:
|
The value of is the equilibrium length of the spring. Since the product |
of |
must be dimensionless, the constant must have units of inverse time |
and must be the frequency of oscillation. By taking the second time derivative of either Equation 1-9 or 1-11 results in the following expression:
8 |
Chapter 1 |
|
By comparing Equation 1-12 with Equation |
l-8b, an expression for |
is |
readily obtained. |
|
|
Since the sine and cosine functions will oscillate from +1 to –1, the constants a and b in Equation 1-9 and likewise the constants A and B in Equation 1-11 are related to the amplitude and phase of motion of the mass. There are no constraints on the values of these constants, and the system is not quantized.
A model can now be developed that more accurately describes a diatomic molecule. Consider two masses,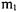 
and 
separated by a spring with a force constant k and an equilibrium length of 
as shown in Figure 1-2. The Hamiltonian is shown below.
Classical Mechanics |
9 |
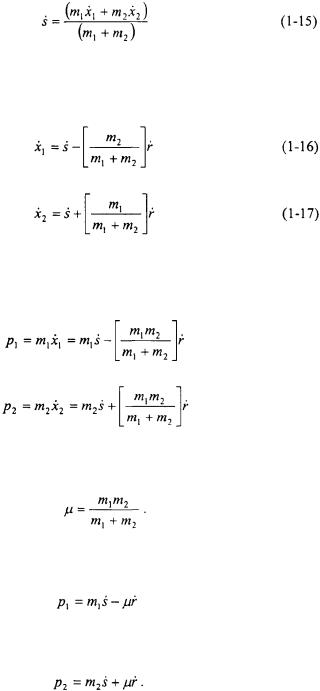
Note that the Hamiltonian appears to be inseparable. Making a coordinate transformation to a center-of-mass coordinate system can make this problem separable. Define r as the displacement of the spring from its equilibrium position and s as the position of the center of mass.
As a result of the coordinate transformation, the potential energy for the system becomes:
Now the momentum 
and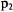 
must be transformed to the momentum in the s and r coordinates. The time derivatives of r and s must be taken and related to the time derivatives of 
and 
10 |
Chapter 1 |
From Equations 1-14 and 1-15, expressions for 
and 
in terms of 
and 
can be obtained.
The momentum terms 
and 
are now expressed in terms of the center of mass coordinates s and r.
The reduced mass of the system, 
is defined as
This reduces the expressions for 
and 
to the following:
and
Classical Mechanics |
11 |
The Hamiltonian can now be written in terms of the center-of-mass coordinate system.
A further simplification can be made to the Hamiltonian by recognizing that the total mass of the system, M, is the sum of 
and 
Recall that the coordinate s corresponds to the center of mass of the system whereas the coordinate r corresponds to the displacement of the spring. This ensures that r and s are separable. It can be concluded that the kinetic energy term
must correspond to the translation of the entire system in |
space. Since it is |
the vibrational motion that is of interest, the kinetic term |
for the translation |
of the system can be neglected in the Hamiltonian. The resulting Hamiltonian that corresponds to the vibrational motion is as follows:
Notice that the Hamiltonian in Equation 1-19 is identical in form to the Hamiltonian in Equation 1-7 solved previously. The solution can be inferred from the previous result recognizing that when the spring is in its equilibrium position 
then 
(refer to Equation 1-14).
12 |
Chapter 1 |
This example demonstrates a number of important techniques in solving mechanical problems. A mechanical problem can at times be made separable by an appropriate coordinate transformation. This will prove especially useful in solving problems that involve circular motion where coordinates can be made separable by transforming Cartesian coordinates to polar or spherical coordinates. Another more subtle point is to learn to recognize a Hamiltonian to which you know the solution. In chemical systems, the Hamiltonian of a molecule will often have components similar to other molecules or model problems for which the solution is known. The ability to recognize these components will prove important to solving many of these systems.
PROBLEMS AND EXERCISES
l.l) Calculate the range of a projectile with a mass of 10.0 kg fired from a cannon at an angle of 30.0° from the horizontal axis with a muzzle velocity of 10.0 m/s.
1.2) Using Hamiltonian mechanics, determine the time it will take a 1.00 kg block initially at rest to slide down a 1.00 m long frictionless ramp that has an angle of 45.0° from the horizontal axis.
1.3) Set up the Hamiltonian for a particle with a mass m that is free to move in the x, y, and z-coordinates that experiences the gravitational potential 
Using Equations 1-5 and 1-6, obtain the equations of motion in each dimension.
1.4) Determine the force constant of a harmonic spring oscillating at 
that is attached to an immovable object at one end the following masses at the other end: a) 0.100 kg; b) 1.00 kg; c) 10.0 kg; and d) 100. kg.
Classical Mechanics |
13 |
1.5) Determine the oscillation frequency of a 
bond that has a force constant of 
1.6) Show that a potential of the general form 
is the same as that for a harmonic oscillator because it can be written as 
Find k, 
and 
in terms of a, b, and c.
Chapter 2
Fundamentals of Quantum Mechanics
Classical mechanics, introduced in the last chapter, is inadequate for describing systems composed of small particles such as electrons, atoms, and molecules. What is missing from classical mechanics is the description of wavelike properties of matter that predominates with small particles. Quantum mechanics takes into account the wavelike properties of matter when solving mechanical problems. The mathematics and laws of quantum mechanics that must be used to explain wavelike properties cause a dramatic change in the way mechanical problems must be solved. In classical mechanics, the mathematics can be directly correlated to physically measurable properties such as force, momentum, and position. In quantum mechanics, the mathematics that yields physically measurable properties is obtained from mathematical operations with an indirect physical correlation.
2.1 THE DE BROGLIE RELATION
At the beginning of the 
century, experimentation revealed that electromagnetic radiation has particle-like properties (as an example, photons were shown to be deflected by gravitational fields), and as a result, it was theorized that all particles must also have wavelike properties. The idea that particles have wavelike properties resulted from the observation that a monoenergetic beam of electrons could be diffracted in the same way a monochromatic beam of light can be diffracted. The diffraction of light is a result of its wave character; hence, there must be an abstract type of wave
14
Fundamentals of Quantum Mechanics |
15 |
character associated with small particles. De Broglie summarized the universal duality of particles and waves in 1924 and proposed that all matter has an associated wave with a wavelength,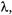 
that is inversely proportional to the momentum, p, of the particle (verified experimentally in 1927 by Davison and Germer).
The constant of proportionality, h, is Planck’s constant. The de Broglie relation fuses the ideas of particle-like properties (i.e. momentum) with wave-like properties (i.e. wavelength). This duality of particle and wave properties will be the theme throughout the rest of the text.
The de Broglie relationship not only provides for a mathematical relationship for the duality of particles and waves, but it also begins to hint at the idea of quantization in mechanics. If a particle is in an orbit, the only allowed radii and momenta are those where the waves associated with the particle will interfere non-destructively as they wrap around each orbit. Momenta and radii where the waves destructively interfere with one another are not allowed, as this would suggest an “annihilation” of the particle as it orbits through successive revolutions.
As mentioned in the introduction to Chapter 1, for any theory to be valid it must predict classical mechanics at the limit of macroscopic particles (called the Correspondence Principle). In the de Broglie relationship, the wavelength is an indication of the degree of wave-like properties. Consider an automobile that has a mass of 1000. kg travelling at a speed of 
The momentum of the automobile is
Dividing this result into Planck’s constant yields the de Broglie wavelength.