
Mueller M.R. - Fundamentals of Quantum Chemistry[c] Molecular Spectroscopy and Modern Electronic Structure Computations (Kluwer, 2001)
.pdf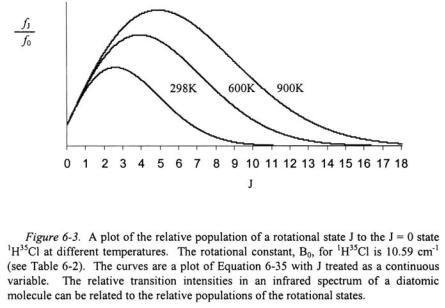
126 |
Chapter 6 |
A plot of the function in Equation 6-35 for  is shown in Figure 6-3. At room temperature (298 K), the rotational states with the highest population are at
is shown in Figure 6-3. At room temperature (298 K), the rotational states with the highest population are at  The peaks with the greatest intensity in an infrared spectrum for
The peaks with the greatest intensity in an infrared spectrum for  will correspond to the change in rotational states of
will correspond to the change in rotational states of 
 and
and  This is confirmed by the spectrum in Figure 6-2. In addition, as the temperature increases, the number of peaks that will appear in the P and R branches of the infrared spectrum increases, and the peaks of greatest intensity will correspond to increasingly larger initial J states.
This is confirmed by the spectrum in Figure 6-2. In addition, as the temperature increases, the number of peaks that will appear in the P and R branches of the infrared spectrum increases, and the peaks of greatest intensity will correspond to increasingly larger initial J states.
The RRHO approximation and analysis of the infrared spectrum of  formulates a picture of the vibration-rotation energy levels of a diatomic molecule. The energy difference between vibrational energy levels is large with respect to the rotational energy levels. A vibrational state
formulates a picture of the vibration-rotation energy levels of a diatomic molecule. The energy difference between vibrational energy levels is large with respect to the rotational energy levels. A vibrational state  will have an infinite manifold of J rotational states. This is depicted in Figure 6- 4.
will have an infinite manifold of J rotational states. This is depicted in Figure 6- 4.

Vibrational/Rotational Spectroscopy of Diatomic Molecules |
127 |

128 |
Chapter 6 |
6.3 VIBRATIONAL ANHARMONICITY
The realistic vibrational potentials of molecules are not strictly harmonic oscillations. The energy differences between vibrational levels are not uniform as predicted by the harmonic oscillator model problem but rather continuously decrease and form a continuum at sufficiently large vibrational eigenstates. In addition, all molecules will dissociate if promoted to a sufficiently high vibrational eigenstate. Vibrational anharmonicity refers to those parts of the stretching potential that are not harmonic, in other words, the parts of the potential that do not vary as the square of the displacement.
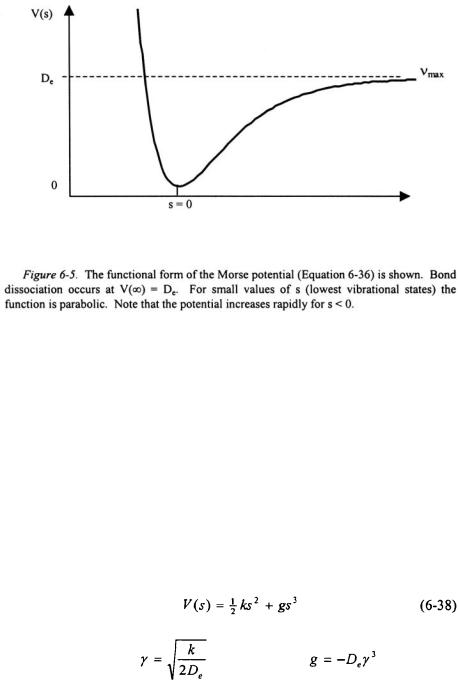
An approximate approach for modeling the anharmonicity of the stretching potential of a diatomic molecule is the Morse potential. The Morse potential is constructed such that  is the depth of the minimum of the curve (related to the dissociation energy of the diatomic molecule) and choosing a parameter
is the depth of the minimum of the curve (related to the dissociation energy of the diatomic molecule) and choosing a parameter  that yields the correct shape of the potential curve.
that yields the correct shape of the potential curve.
The coordinate s is the displacement of the bond from its equilibrium position  as defined in Equation 6-11. The qualitative form of the Morse potential is shown in Figure 6-5. At
as defined in Equation 6-11. The qualitative form of the Morse potential is shown in Figure 6-5. At  the potential is zero. As s approaches infinity, the value of the potential approaches
the potential is zero. As s approaches infinity, the value of the potential approaches  indicating dissociation of the bond. As a result, the Morse potential has a finite number of states
indicating dissociation of the bond. As a result, the Morse potential has a finite number of states  such that when
such that when  the bond is at the highest possible vibrational state before dissociation. For
the bond is at the highest possible vibrational state before dissociation. For  representing compression of the bond, the Morse potential rises very rapidly as in a real molecule. The Morse potential can be compared to the harmonic oscillator potential by writing Equation 6-36 in an infinite power series in terms of s.
representing compression of the bond, the Morse potential rises very rapidly as in a real molecule. The Morse potential can be compared to the harmonic oscillator potential by writing Equation 6-36 in an infinite power series in terms of s.
Vibrational/Rotational Spectroscopy of Diatomic Molecules |
129 |
The first term in Equation 6-37 is harmonic and the subsequent third, fourth, and higher order terms are varying degrees of anharmonicity.
In infrared spectroscopy of diatomic molecules, the vibrational motion is generally limited to the first two vibrational states of a diatomic molecule whereby the displacement of the bond is near the minimum (i.e. small values of s). As a result, it is reasonable as a first approximation to confine the anharmonicity to the third order term of Equation 6-37. The potential can be represented by a third order polynomial such that the first term is the same as in the harmonic oscillator model problem.
where |
and |

130 |
Chapter 6 |
Perturbation theory can now be used to determine the correction to the energy eigenvalues for vibrational motion. The first-order perturbing Hamiltonian is the cubic term in Equation 6-38.
The first-order correction to the energy is calculated by using Equation 4-13.
The first-order correction to the energy for all states is zero. The secondorder corrections to the energy due to the  term are computed using Equation 4-18b.
term are computed using Equation 4-18b.
The general solution to the second order correction to the energy is as follows:
or
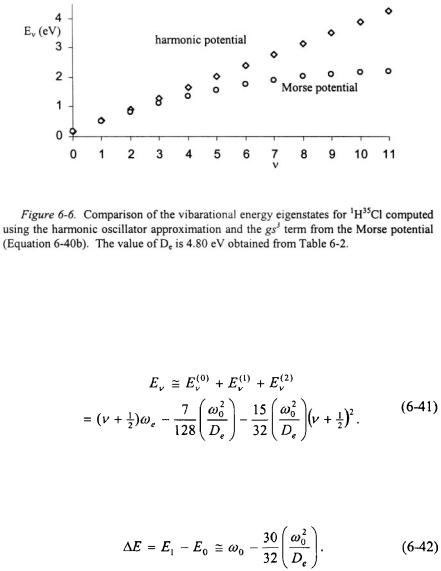
As can be seen in Equation 6-40b, the effect of the anharmonic term  is to lower the energy for each vibrational energy eigenstate relative to the harmonic oscillator. This is shown in Figure 6-6 for
is to lower the energy for each vibrational energy eigenstate relative to the harmonic oscillator. This is shown in Figure 6-6 for  The energy levels for an anharmonic oscillator become more closely spaced with increasing energy.
The energy levels for an anharmonic oscillator become more closely spaced with increasing energy.
Vibrational/Rotational Spectroscopy of Diatomic Molecules |
131 |
The energy of a vibrational eigenstate using the cubic term of the Morse potential to a second-order energy correction is as follows:
For a change in vibrational states of  (as in a typical infrared spectrum of a diatomic molecule), Equation 6-41 becomes:
(as in a typical infrared spectrum of a diatomic molecule), Equation 6-41 becomes:
Equation 6-42 suggests that the dissociation energy,  of a diatomic molecule can be estimated from an infrared spectrum. The dissociation energy of a diatomic molecule,
of a diatomic molecule can be estimated from an infrared spectrum. The dissociation energy of a diatomic molecule,  is defined as the difference between the depth of the potential well,
is defined as the difference between the depth of the potential well,  and the ground-state energy,
and the ground-state energy, 

132 |
Chapter 6 |
The Morse potential is only an approximation to an actual molecular oscillation. A more accurate representation is obtained via a polynomial that can be fitted to experimental data.
The term  is the first (equilibrium) anharmonicity constant,
is the first (equilibrium) anharmonicity constant,  is the second anharmonicity constant, and so on.
is the second anharmonicity constant, and so on.
6.4 CENTRIFUGAL DISTORTION
The energy eigenvalue expression for the vibration-rotation of a diatomic molecule can be improved by including more terms from Equation 6-18. If one additional term is added, the approximation becomes:
This makes the effective potential from Equation 6-17 as follows:
where |
and |
If the vibrational potential is assumed to be harmonic, the effective potential becomes the following quadratic polynomial:
The two-body vibrating/rotating Schroedinger equation becomes:

Vibrational/Rotational Spectroscopy of Diatomic Molecules |
133 |
One method for solving Equation 6-46 is to use perturbation theory. The term in the brackets in Equation 6-46 can be recognized as the Schroedinger equation for the RRHO approximation (Equation 6-19), and the term bs can be taken as a first-order perturbation. The first-order and higher order corrections to the energy eigenvalues to the RRHO approximation can then be computed using Perturbation Theory.
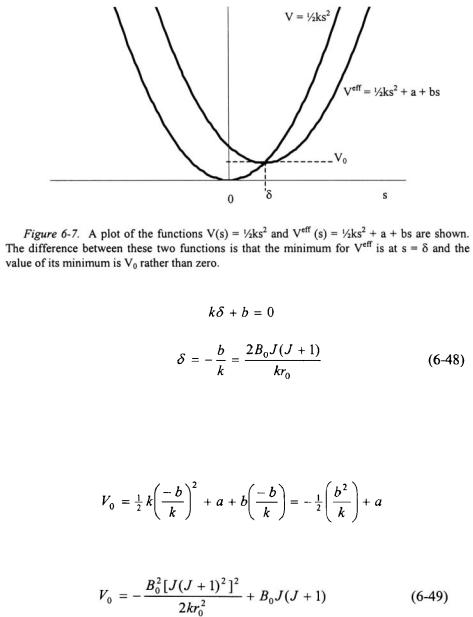
An easier approach to solving Equation 6-46 is recognize that the effective potential in Equation 6-45 is still a quadratic equation resulting in a parabola. As can be seen in Figure 6-7, the only difference between parabola  and the parabola from the effective potential in Equation 6-45 is that the minimum potential is no longer at
and the parabola from the effective potential in Equation 6-45 is that the minimum potential is no longer at  The minimum is shifted by amount
The minimum is shifted by amount  and the minimum potential is now
and the minimum potential is now 
Since the minimum of a parabolic potential of a harmonic oscillator is shifted, the effect is to add to each energy eigenvalue. As a result, each energy eigenvalue has a term  added to it.
added to it.
The wavefunctions  that satisfy Equation 6-47 are the same as for a harmonic oscillator since the Schroedinger equation has the same functional form. Since the value of
that satisfy Equation 6-47 are the same as for a harmonic oscillator since the Schroedinger equation has the same functional form. Since the value of 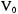 represents the minimum of
represents the minimum of  at
at  the value of
the value of  is determined by taking the derivative of
is determined by taking the derivative of  (Equation 6-45) and setting the derivative equal to zero.
(Equation 6-45) and setting the derivative equal to zero.
134 |
Chapter 6 |
The value of  is determined by substituting Equation 6-48 into Equation 6- 45.
is determined by substituting Equation 6-48 into Equation 6- 45.
or
The energy eigenvalues are as follows:
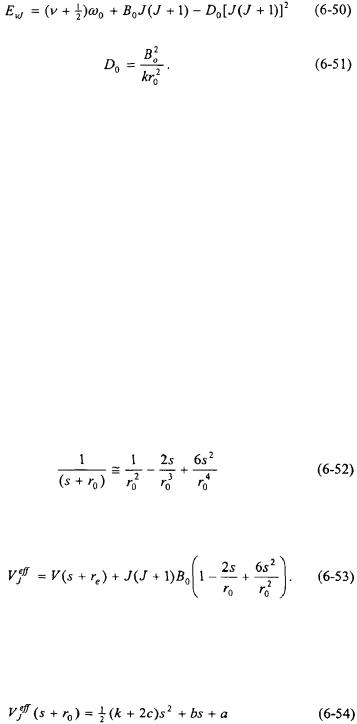
Vibrational/Rotational Spectroscopy of Diatomic Molecules |
135 |
where
The energy eigenvalue expression in Equation 6-50 is the same as for the RRHO approximation (Equation 6-25) except for the last term. The term  is called the centrifugal distortion constant. Note that it does have the same symbol as dissociation energy; however, its context will indicate whether it represents dissociation energy or the centrifugal distortion constant.
is called the centrifugal distortion constant. Note that it does have the same symbol as dissociation energy; however, its context will indicate whether it represents dissociation energy or the centrifugal distortion constant.
The physical interpretation of centrifugal distortion is that as a result of the rotation of the diatomic molecule, the “spring” representing the bond between the atoms is stretched. This increases the effective equilibrium bond length of the molecule lowering the energy of each eigenstate. The effect of centrifugal distortion increases with increasing value of J.
6.5 VIBRATION-ROTATION COUPLING
Including an additional term can make a further improvement to the truncation made in Equation 6-18.
The effective potential becomes as follows:
If the original vibrational potential,  is taken to be harmonic, the effective potential has the same form as in Equation 6-45 with a different effective force constant:
is taken to be harmonic, the effective potential has the same form as in Equation 6-45 with a different effective force constant:
