Mueller M.R. - Fundamentals of Quantum Chemistry[c] Molecular Spectroscopy and Modern Electronic Structure Computations (Kluwer, 2001)
.pdf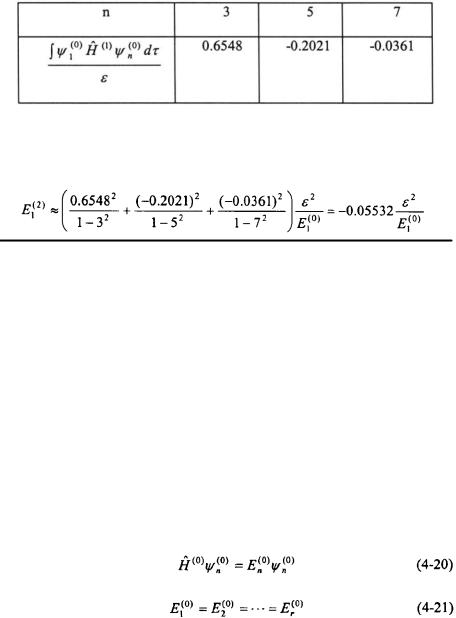
76 |
Chapter 4 |
Since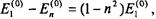 
the second-order energy correction for the ground-state of the perturbed system becomes:
4.3TIME-INDEPENDENT DEGENERATE PERTURBATION THEORY
The non-degenerate perturbation expressions that have been developed in the previous section will result in zero denominators for degenerate systems. As a result, the approach used to obtain the expressions for the various orders of corrections for a degenerate system must be modified from the approach used in non-degenerate systems.
Consider an unperturbed system where a given energy level n has an r- fold degeneracy. This means that there are r wavefunctions that will result in the same energy, 
when applied to the Hamiltonian, 
In this notation scheme, the n refers to the various degenerate states 
Now suppose this degenerate system experiences a perturbation. The Hamiltonian for this perturbed system is 
and the wavefunctions for the perturbed system are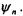 
The wavefunctions 
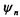may be non-degenerate, have a fraction of the degeneracy, or in some cases no change in the degeneracy relative to the unperturbed system. The change in degeneracy in
Techniques of Approximation |
77 |
the perturbed system has to do with the nature and symmetry of the perturbation relative to the unperturbed wavefunctions. For the perturbed system:
Equation 4-22 for the perturbed degenerate system is analogous to Equation 4-6 for the non-degenerate perturbed system. A natural assumption at this point is that the zero-order wavefunction of 
is 
as in Equation 4-20. If the eigenvalue 
is non-degenerate, then the assumption is certainly true as there is a unique normalized eigenfunction that will satisfy Equation 4-20 (this is precisely the approach used in the previous section). However, if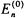 
has a degeneracy of r, then there are r normalized eigenfunctions along with an infinite number of other normalized linear combinations of the r functions that will satisfy Equation 4-20.
For the unperturbed system, any normalized linear combinations of the r unperturbed wavefunctions are acceptable solutions; however for the perturbed system, only certain normalized linear combinations form the correct zero-order perturbed (unperturbed) wavefunctions 
The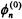 
wavefunctions depend on the type of perturbation that the system experiences. The perturbed energy eigenvalues and wavefunctions can now be written in terms of orders of 
78 |
Chapter 4 |
For an r-degenerate system, there will be r perturbed wavefunctions, 
and r energy eigenvalues, 
Equations 4-22, 4-25, and 4-26 can now be substituted into the Schroedinger equation for the perturbed system (Equation 4-23).
Ordering the orders of the coefficients of 
yields the following:
The same procedure as in the non-degenerate case is now continued to obtain the first-order correction to the energy. Equation 4-28 is now multiplied by the complex conjugate of one the unperturbed degenerate wavefunctions, 
and integrated over all space.
Since 
is hermitian (see Section 4.2),
Techniques of Approximation |
79 |
The expression for |
in Equation 4-24 can now be substituted into |
Equation 4-29. |
|
The degenerate unperturbed wavefunctions 
orthonormal. As a result, the relationship employed (see Equation 2-24).
can always be chosen to be for orthonormality can be
The orthonormality relationship can now substituted into Equation 4-30.
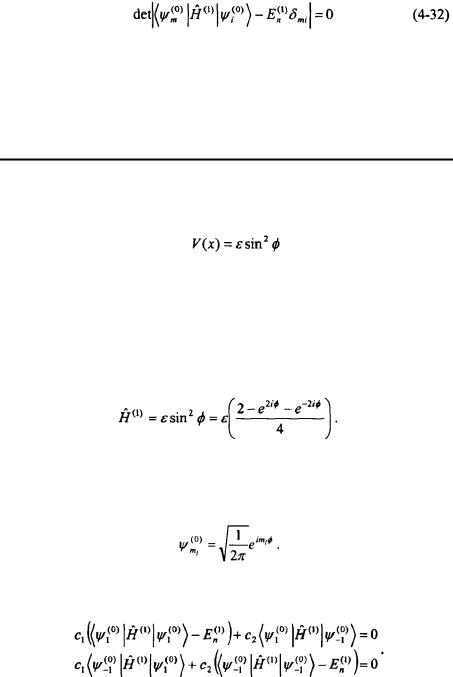
The expression in Equation 4-31 results in r homogeneous equations.
In order for these equations to have a non-trivial solution, the determinant of the coefficients must be equal to zero. The resulting expression is called the secular equation.
80 |
Chapter 4 |
The first-order correction to determinant. The coefficients Equation 4-31.
the energy is determined by solving the 
can then be found by substituting back into
Example 4-6
Problem: The Particle-on-a-Ring experiences the following potential:
Determine the first-order energy corrections to the degenerate 
states and the value of the coefficients for the zero-order wavefunctions, 
Solution: The first-order perturbing Hamiltonian for the problem can be written for convenience in the following form:
The unperturbed wavefunctions for the Particle-on-a-Ring are given as (see Equation 3-7):
The following equations must be solved:
The following integral needs to be solved:
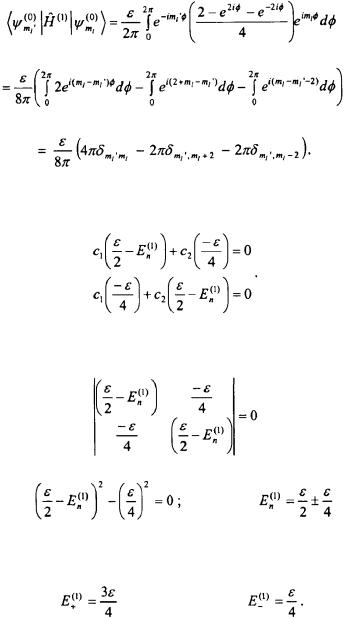
Techniques of Approximation |
81 |
This results in the following equations:
The non-trivial solution is when the following determinant is equal to zero.
This results in the following first-order energy corrections:
Now all that remains is to determine the value of the coefficients for 
for the two resulting states. Since 
must be normalized, one equation that must be satisfied is
82 |
Chapter 4 |
As a result of the perturbation, the degeneracy is lost for the 
state for the Particle-on-a-Ring.
PROBLEMS AND EXERCISES
4.1) Determine the normalized and optimized ground-state wavefunction for the one-dimensional Particle-in-a-Box using the following trial wavefunction:
where p is an adjustable parameter and N is the normalization constant. Compare the ground-state energy obtained using this trial function to the true ground-state energy.
Techniques of Approximation |
83 |
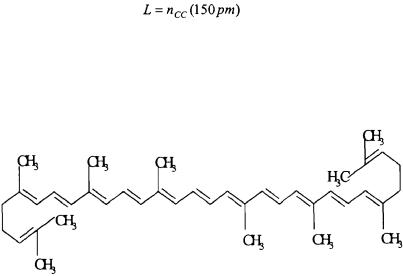
4.2) A simple model for predicting ultra-violet/visible absorption spectra of conjugated polyenes is the free-electron molecular orbital model. In this model, the electrons of the conjugated 
system are free to travel the length of the conjugated carbon chain. In this model, the 1- dimensional particle-in-a-box model problem can be used to simulate the molecular orbitals of the electrons in the conjugated chain. The length of the box, L, is equal to the length of the conjugated carbon chain.
The value 
corresponds to the number of carbon/carbon bonds in the conjugated chain. The electrons can be ordered two at a time in each energy level. In this problem, we will consider lycopene.
a.Determine the energy of the transition from the lowest occupied to the first unoccupied energy level for lycopene. Determine the wavelength
needed for this transition 
The experimental value for lycopene is 474 nm.
b.The value obtained from part (a) above is not in good agreement with what is obtained experimentally. This is in part because the potential on the electron is not zero or constant. The potential can be improved by having it change sinusoidally along the polyene chain. Choose a sine function that will have an appropriate periodicity over lycopene and treat it as a first-order perturbation. Repeat the computations from part (a) using up to a second-order energy correction.
84 |
Chapter 4 |
4.3) Consider a Particle-in-a-Box with a ramp-like potential that increases from 
to 
a.Determine up to the second-order energy correction along with a firstorder wavefunction correction for the 
and 
states.
b.Suppose the potential in part (a) is due to gravity because the box is vertical. Apply the results from part (a) for an electron at the surface of the Earth.
4.4) Determine the first-order energy corrections for the 
states for the Particle-on-a-Ring problem when
Find the values of the zero-order wavefunction coefficients.
Chapter 5
Particles Encountering a Finite Potential Energy
The systems we have studied so far have all involved particles confined to a limited region of space such as a box, circle, or a sphere via infinite potentials. In the case of a box, it is explicitly stated that the potentials at the “walls” of the box are infinite. Though not explicitly stated, in order to confine a particle to a circle or a sphere of constant radius r, the potential must be infinite for anyplace outside the circle or sphere. Removing the requirement of infinite potential at a given point has the effect of no longer being able to completely contain a particle into any limited region of space even if the potential exceeds the energy of the particle. In addition, quantum mechanics predicts that a particle can be reflected by a potential even though its energy is in excess of that potential. These phenomena are entirely a quantum mechanical result due to the wave nature of matter.
5.1 HARMONIC OSCILLATOR
The harmonic oscillator is used as a simple model for the vibrational motion of atoms along bonds in molecules. This will in turn be used to model infrared absorption spectroscopy in the next chapter.
Consider a spring with a force constant k with a Hooke’s law potential anchored at one end and attached to a mass of m on the other end as shown in Figure 1-1. The particle is confined to travel only along the x-coordinate, and for convenience, the equilibrium position of the spring (point of zero potential energy) is at 
The Hamiltonian for the particle becomes:
85