Всемирное тяготение

6 Закон всемирного тяготения

1. В природе исключительную роль играют силы тяготения. Закон, которому они подчиняются, - закон всемирного тяготения – открыт Ньютоном в 1687 году.

Согласно этому закону любые две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих точек, обратно пропорциональной квадрату расстояния между ними и направленной по прямой, соединяющей эти точки (рис.13).

Численное значение силы тяготения

(6.1)

здесь: m₁ и m₂ - массы материальных точек; r - расстояние между точками;  - гравитационная постоянная (размерный коэффициент пропорциональности, зависящий от выбора единиц измерения, F, m и r)

2. Чтобы придать закону тяготения векторный вид, проведём от первой точки ко второй радиус-вектор 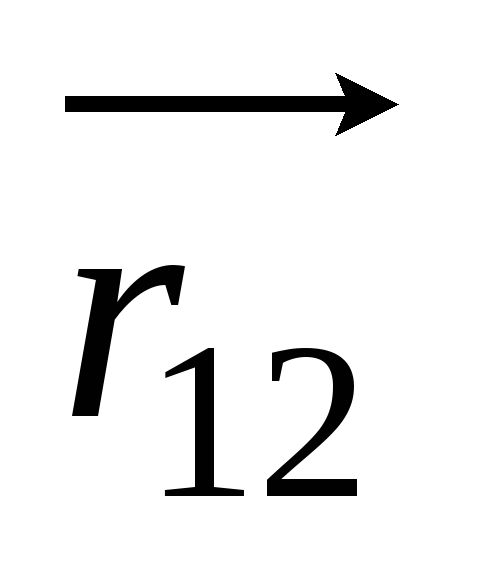и умножим правую

часть (6.1) на единичный вектор этого направления . Тогда сила, действующая на второе тело со стороны первого, будет равна:

Знак “минус” означает, что направления радиус-вектора и силыпротивоположны.

3. Силы тяготения подчиняются третьему закону Ньютона: они равны по величине и противоположны по направлению:

4. Силы тяготения – всепроникающие силы: от них нельзя экранироваться, их нельзя усилить или ослабить. Материальная среда, в которой находятся взаимодействующие тела, на величину и направление силы тяготения никакого влияния не оказывает.

5. Формула (6.1) позволяет найти силу гравитационного взаимодействия между материальными точками.

Чтобы рассчитать силу тяготения между телами, размеры которых соизмеримы с расстояниями между ними, поступают следующим образом. Оба тела разбивают на столь малые элементы, что каждый такой элемент можно считать материальной точкой. Выбирают в первом теле произвольный элемент и определяют результирующую силу, действующую на него со стороны всех элементов второго тела, иначе говоря, определяют силу, с которой второе тело в целом притягивает к себе этот выделенный элемент. Затем проделывают то же самое для остальных элементов первого тела, после чего находят полную геометрическую сумму сил, найденная сумма и будет представлять собой силу, с которой второе тело действует на первое. С такой же по величине, но противоположной по направлению силой первое тело действует на второе. Расчёт показывает, что математическое выражение для силы тяготения, действующей между однородными шарами, шарами с плотностью, зависящей от r (r – расстояние от центра шара), между сферическими слоями будет совпадать с (6.1), если под r понимать расстояние между центрами этих тел (рис.14). Закон тяготения справедлив также для тел, одно из которых - однородный шар, а другое - материальная точка (с этим случаем мы имеем дело, например, при расчёте силы, с которой Земля притягивает к себе находящиеся на её поверхности тела).

6. В формулу закона тяготения входит масса. Масса уже фигурировала в уравнениях механики, в частности, в выражении второго закона Ньютона. Там она характеризовала инерционные свойства тел и называлась “инертной”.

Роль массы в законе тяготения иная. Здесь она определяет силу гравитационного взаимодействия материальных тел, т.е. является ме-

рой их гравитационных свойств. Эту массу, в отличие от “инертной”, называют “гравитационной” или “тяжёлой”.

Различать гравитационную и инертную массу в настоящее время нет необходимости. Многими, весьма тонкими экспериментами (Бессель, Этвеш, Крылов и др.) установлено, что инертная и гравитационная массы с точностью до 10^-8 совпадают. Это, в сущности, одна и та же физическая величина, по-разному проявляющая себя в различных физических явлениях. С одной стороны, масса - это мера инерционных свойств, с другой - мера гравитационных свойств.

7. Гравитационная постоянная  является универсальной константой, не зависящей от природы взаимодействующих тел. Эта величина

численно равна силе, с которой притягиваются друг к другу две материальные точки единичной массы, расположенные на единичном расстоянии друг от друга: если | m₁ |= | m₂ | = 1, | r | = 1, то |  | = | F |.

Численное значение  было впервые определено У. Кавендишем

в 1797 г.

Это значит, что два точечных тела (или шара) массой по 1кг каждый, расположенные на расстоянии 1м друг от друга, притягиваются с силой 6,6710^-11 Н.

Необычайно малая величина  указывает на то, что гравитационное взаимодействие становится заметным только в случае очень больших масс. В механике таких объектов, как атомы и молекулы, гравитационные силы практически не играют никакой роли.

Движение же таких макроскопических тел, как звёзды, Солнце, планеты, Луна, спутники (после того, как выключены двигатели) полностью управляется силами тяготения.