III. Упругие столкновения

1. Столкновение называется абсолютно упругим, если по его завершении тела полностью восстанавливают свою первоначальную форму и в их внутреннем состоянии не происходит каких-либо изменений, если сохраняется суммарная механическая энергия тел.

2. Столкновения обычных, макроскопических тел в реальных условиях всегда бывают в той или иной степени неупругими, ибо они всегда сопровождаются нагреванием тел, образованием акустических волн и т.д., т.е. превращением части механической энергии тел в другие виды. Однако в некоторых случаях столкновения макроскопических тел можно с достаточной степенью точности считать абсолютно упругими (например, столкновение шаров из слоновой кости или закалённой стали).

Особо важную роль упругие столкновения играют в физике атомных явлений. Так, столкновения молекул газа друг с другом и со стенками сосуда, в который газ заключён, можно уподобить соударениям абсолютно упругих шаров. Упруго рассеиваются  - частицы при прохождении через тонкие плёнки вещества (опыты Резерфорда), рентгеновские кванты при взаимодействии с электронами и т.д.

3. Рассмотрим абсолютно упругое центральное столкновение двух шаров. Пусть массы шаров m₁ и m₂. Шары двигаются один вслед за другим (первый шар догоняет второй) и перед столкновением имеют скорости и . Во время столкновения шары деформируются, силы упругой деформации изменяют скорости шаров. Обозначим скорости шаров после столкновения и

Полагая, что шары образуют замкнутую систему, применим к ним закон сохранения импульса:

(12.11)

Пусть массы шаров таковы, что и после соударения они продолжают двигаться в том же направлении, в каком двигались до столкновения. Тогда соотношение (12.11) в проекциях запишется так:

(12.12)

Детальный анализ деформации шаров в процессе упругого столкновения весьма сложен. Но этот анализ, в принципе, и не нужен. Так как шары полностью восстанавливают свою первоначальную форму, и в их внутреннем состоянии не происходит изменений, то закон сохранения энергии сводится к сохранению кинетической энергии:

(12.13)

Решая уравнения (12.12) и (12.1З) совместно (это следует проделать самостоятельно), получим:

(12.14) (12.15)

4. Рассмотрим некоторые частные случаи:

а) Массы шаров равны: m₁ = m₂ = m. Тогда U₁=₂ и U₂=₁. Шары просто обмениваются своими скоростями.

Если до столкновения второй шар покоился (₂=0), то после столкновения он начинает двигаться со скоростью первого шара U₂=₁, а первый шар останавливается U₁=0

б) Масса второго шара значительно больше массы первого m₂>>m₁. Разделим числитель и знаменатель соотношений (12.14) и (12.15) на m₂:

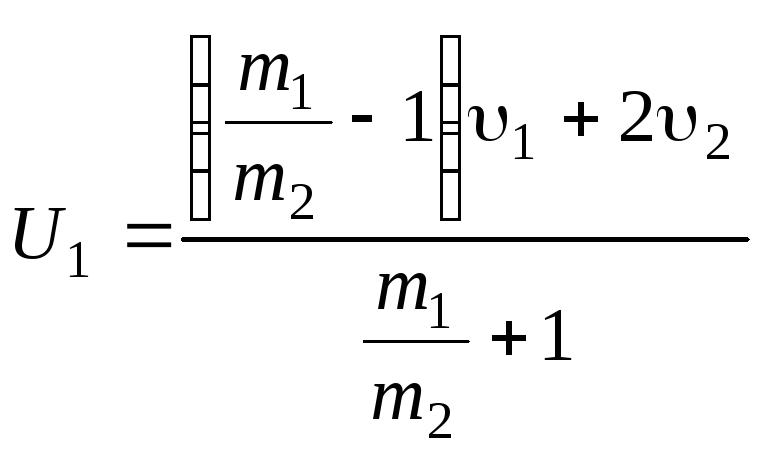и

Отношением можно пренебречь. Тогда и

Вывод: при упругом центральном столкновении шара малой массы с шаром большой массы скорость шара большей массы практически не изменяется. Если ₂=0 (массивный шар покоится), то U₁-, т.е. шар малой массы при упругом ударе отскакивает от массивного неподвижного шара со скоростью, почти равной по величине и противоположной по направлению той скорости, с которой он ударяется. При этом лёгкий шар практическине передаёт свою кинетическую энергию массивному шару.

Полученный вывод можно применить к упругому удару шара о неподвижную стенку, перпендикулярную направлению движения шара (с этим случаем мы сталкиваемся, например, при расчёте давления, оказываемого молекулами газа на стенки сосуда).

Найдём изменение импульса шара при таком упругом отражении:

Такой же по величине, но противоположной по знаку импульс получит стенка.

в) Шары двигаются в одном направлении. m₁<<m₂, но ₁>>₂.

Тогда

Малый шар отскакивает от большего со скоростью, меньшей первоначальной на величину 2₂.

Нечто подобное происходит в цилиндре с газом при расширении газа. Молекулы, ударяющиеся об удаляющийся поршень, теряют свою скорость и, следовательно, кинетическую энергию. Эти “потери” проявляются в охлаждении газа.

г) Шары двигаются навстречу друг другу. m₁<<m₂, ₁>>₂. Тогда, проекция скорости₂ на положительно выбранное направление отрицательна.

Малый шар отскакивает от большого со скоростью, превышающей ту, с которой он ударяется о большой шар на величину 2₂.

Нечто подобное происходит в цилиндре с газом при сжатии газа. Молекулы, ударяющиеся о надвигающийся поршень, увеличивают свою скорость и кинетическую энергию, что проявляется в нагревании газа.