П5. Движущееся поле. Прибор и эксперимент

Введя понятие движения поля и применяя его для создания физической картины мира, мы разработали метод измерения скорости движения поля и построили прибор, измеряющий эту скорость. Прибор и метод разработаны для магнитного поля, хотя мы понимаем, что в реальности магнитного поля, как самостоятельного объекта, не существует. Тем не менее в целях наглядности весьма удобно пользоваться представлением о самостоятельно существующем «магнитном поле». Можно воспользоваться для создания прибора непосредственно определением, введенным в главе 1. Предложенная там процедура предполагает фиксацию величины напряжённости поля в какой-то момент времени и затем, через фиксированный интервал времени, быстрый поиск той координаты, в которой обнаруживается то самое значение напряжённости поля, которое было ранее зафиксировано. Для мысленных экспериментов и рассуждений такая процедура вполне удобна, так как мысленно мы можем перемещаться и измерять напряжённости с любой скоростью, вплоть до бесконечной. На практике же это невозможно, поэтому требуется модифицировать процедуру измерения скорости движения поля с целью получения достаточной точности при простой технической реализации прибора. К счастью, модификация метода оказывается почти очевидной.

Используемый в приборе метод предполагает расположение двух датчиков магнитного поля (датчики Холла, например) на небольшом фиксированном расстоянии R друг от друга (рис. П5.1).

Рис. П5.1. Расположение датчиков в методе измерения скорости движения поля

Показания первого (ближнего к источнику движущегося поля) датчика

Показания второго датчика снимаются синхронно с показаниями первого и обозначаются как B2 . Обе величины запоминаются. Далее обе напряжённости измеряются с высокой

напряжённость уменьшается, то, наоборот, величина на первом датчике достигнет запомненной ранее величины B2 . Поскольку нам неизвестно априорно будет

напряжённость поля уменьшаться или увеличиваться, то мы делаем и то и другое одновременно, прекращая измерения как только величина поля, хотя бы на одном из датчиков, достигнет запомненной ранее величины «противоположного» датчика. При этом мы получаем информацию о том, нарастает напряжённость поля или же убывает. И о

251

равное R . Нетрудно догадаться, как теперь определить скорость движения поля vB :

Можно заметить, что в предложенном методе мы заменили поиск в пространстве «поиском» во времени. В рамках наших представлений это возможно, поскольку движение полей мало чем отличается (за исключением особых случаев) от движения механических объектов. Остаётся определить, что делать, если равенство напряжённостей в описанной выше процедуре не достигнуто за время t . Один из вариантов - объявить, что скорость в этом случае пренебрежимо мала и назначить её равной нулю. Например, если расстояние между датчиками равно 1 см, а время t =0.1 с, то минимальная измеряемая скорость составит 0.1 м/с. Теперь, измерив скорость, следует вывести её из измерительного прибора в виде, например, уровня напряжения Uv . В соответствии с

описанной процедурой был разработан и изготовлен прибор - измеритель скорости движения магнитного поля (рис. П5.2).

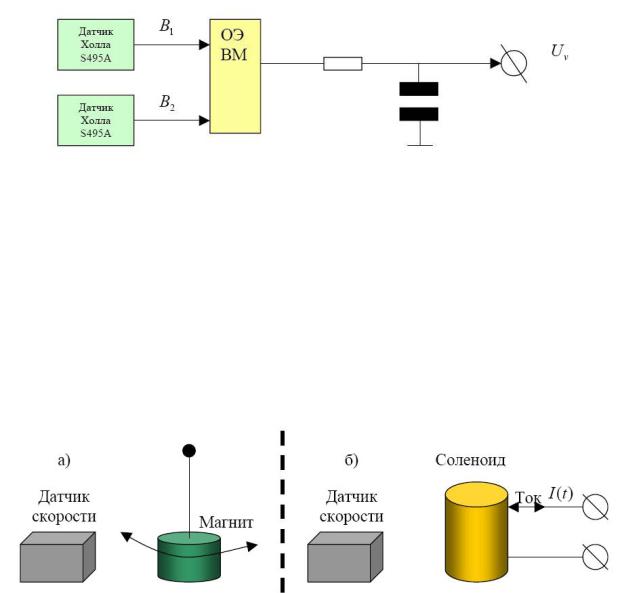
Рис. П5.2. Блок-схема измерителя скорости движения магнитного поля

Построив прибор, мы провели два наглядных эксперимента, показывающих, что переменное магнитное поле является движущимся полем. В первом эксперименте мы расположили постоянный магнит в виде маятника, подвесив его на тонком длинном рычаге, способном двигаться только в одной плоскости (рис. П5.3а). Отклонив магнит на не слишком большую величину, отпускаем его и снимаем показания на выходе прибора. Магнитное поле постоянного магнита движется вместе с самим магнитом, следовательно, скорость движения поля должна быть равна просто механической скорости движения маятника относительно прибора. Поскольку колебания маятника хорошо поддаются рассчету и изменения его скорости от времени известны, сравниваем эксперимент с рассчетом. Видим (Рис. П5.4а), что изменения скорости движения поля от времени носят почти синусоидальный характер, что и следовало ожидать.

Рис. П5.3. Схема экспериментов с измерителем скорости движения поля

252

Рис. П5.4а. Результаты экспериментов с измерителем скорости движения поля для случая механических колебаний подвешенного магнита. Вверху показания разнесённых датчиков магнитного поля от времени, внизу значения скорости. Скорость ограничена

253

Рис. П5.4б. Результаты экспериментов с измерителем скорости движения поля для случая неподвижного соленоида с переменным током. Вверху показания разнесённых датчиков магнитного поля от времени, внизу значения скорости. Скорость периодически «устремляется в бесконечность»

Видим (рис. П5.4б), что график изменения скорости движения поля от времени вполне соответствует соотношению:

Таким образом, прибор, верно определяющий скорость движения поля в случае простого механического движения источника поля, показывает, что переменное во времени поле даже неподвижного источника также обладает скоростью, зависящей от времени, т.е.

движется.

На рис. П5.6 приведена фотография прибора, использовавшегося для вышеописанных экспериментов.

254

Рис. П5.5. Фотография действующего макета датчика скорости движения магнитного поля. Цифровой дисплей при работе отображает расстояние до источника магнитного поля

255