Глава 9. Элементарные заряды. Электрон и протон

§ 9.1. Электромагнитная масса и заряд. Вопрос о сущности заряда

В главе 5 мы выяснили механизм возникновения инерции, объяснили, что же такое «инерционная масса» и какие электрические явления и свойства элементарных зарядов определяют её. В главе 7 мы проделали всё то же самое для явления тяготения и «гравитационной массы». Выяснилось, что и инерцию и тяготение тел определяют геометрический размер элементарных частиц и их заряд. Поскольку геометрический размер есть понятие привычное, то в основе таких фундаментальных явлений, как инерция и гравитация, оказывается лежащей лишь одна малоизученная сущность - «заряд». До сих пор понятие «заряд» является загадочным и почти мистическим. Сначала учёные имели дело лишь с макроскопическими зарядами, т.е. зарядами макроскопических тел. В начале изучения электричества в науке использовались представления о незримых «электрических жидкостях», избыток или недостаток которых и приводит к электризации тел. Долгое время споры шли лишь о том, одна это жидкость или их две: положительная и отрицательная. Затем выяснили, что существуют «элементарные» носители заряда электроны и ионизированные атомы, т.е. атомы с избыточным электроном, либо недостающим электроном. Ещё позже были обнаружены «самые элементарные» носители положительного заряда – протоны. Затем выяснилось, что «элементарных» частиц много и многие из них обладают электрическим зарядом, причём по величине заряд этот всегда

кратен некоторой минимальной обнаруживаемой порции заряда q0 ≈1.602 10−19 Кл. Эта

порция и названа была «элементарным зарядом». Заряд определяет меру участия тела в электрических взаимодействиях и, в частности, взаимодействиях электростатических. На сегодняшний день вразумительных объяснений, что же такое элементарный заряд не существует. Любые рассуждения на тему того, что заряд состоит из других зарядов (например, кварков с дробными величинами зарядов), это не объяснение, а схоластическое «замыливание» вопроса.

Давайте попробуем подумать о зарядах сами, пользуясь тем, что мы уже установили ранее. Вспомним, что главный закон, установленный для зарядов, есть закон Кулона: сила взаимодействия между двумя заряженными телами прямо пропорциональна произведению величин их зарядов и обратно пропорциональна квадрату расстояния между ними. Получается, что если мы выведем закон Кулона из каких-либо конкретных уже изученных физических механизмов, то тем самым сделаем шаг в понимании сущности зарядов. Мы уже говорили о том, что элементарные заряды в части взаимодействия с внешним миром вполне определяются своим электрическим полем: его структурой и его движением. И говорили, что после объяснения инерции и гравитации в элементарных зарядах ничего, кроме движущегося электрического поля, и не осталось. А электрическое поле есть не что иное, как возмущённые состояния вакуума, эфира, пленума. Ну, так будем же последовательны и попытаемся свести электрон и его заряд к движущемуся полю! Мы уже догадались в главе 5, что протон полностью подобен электрону, за исключением знака заряда и геометрического размера. Если, сведя электрон к движущемуся полю, мы увидим, что мы можем объяснить и знак заряда и независимость количества заряда частиц от размера, то наша задача будет выполнена, хотя бы в первом приближении.

177

§ 9.2. Странные токи и странные волны. Плоский электрон

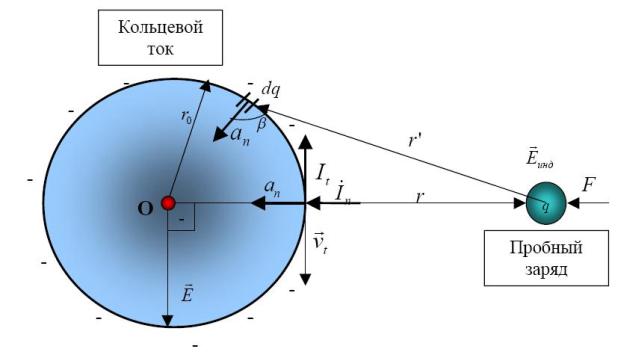
Для начала рассмотрим крайне упрощённую модельную ситуацию (рис. 9.1) кольцевого заряда, движущегося по круговой траектории радиуса r0 . И пусть он в целом

электронейтрален, т.е. в его центре размещён противоположный по знаку заряд. Это так называемый «плоский электрон». Мы не утверждаем, что реальный электрон именно таков, мы лишь пытаемся пока понять, можно ли получить электрически нейтральный объект, эквивалентный свободному элементарному заряду в плоском, двумерном случае. Попробуем создать наш заряд из связанных зарядов эфира (вакуума, пленума). Пусть, для определённости, заряд кольца отрицателен, а движение кольца происходит по часовой стрелке (рис. 9.1). В этом случае ток It течёт против часовой стрелки. Выделим малый

элемент кольцевого заряда dq и припишем ему малую длину dl . Очевидно, что в каждый момент времени элемент dq движется с тангенциальной скоростью vt и нормальным ускорением an . С таким движением мы можем ассоциировать полный ток элемента dI –

величину векторную. Эту величину можно представить как постоянный по величине тангенциальный ток dIt , постоянно «поворачивающий» своё направление с течением

времени, то есть – ускоренный. То есть имеющий нормальное ускорение dI&n . Трудность

дальнейшего рассмотрения связана с тем, что до сих пор в физике рассматривались в основном такие переменные токи, чьё ускорение лежало на одной прямой с направлением самого тока. В данном случае ситуация иная: ток перпендикулярен своему ускорению. И что же? Разве это отменяет твёрдо установленные ранее законы физики?

Рис. 9.1. Кольцевой ток и его силовое действие на пробный заряд

Так же как с самим элементарным током связано его магнитное поле (согласно закону Био-Савара-Лапласа), так и с ускорением элементарного тока связано электрическое поле индукции, как показано нами в предыдущих главах. Эти поля оказывают силовое действие F на внешний заряд q (рис. 9.1). Поскольку радиус r0 конечен, то действия

элементарных токов правой (по рисунку) половины кольца не могут быть полностью скомпенсированы противоположным действием элементарных токов левой половины.

178

Таким образом, между кольцевым током I и внешним пробным зарядом q должно

возникать силовое взаимодействие.

В результате мы получили, что мы можем умозрительно создать объект, который в целом будет совершенно электронейтрален по построению, но содержать в себе кольцевой ток. Что же такое кольцевой ток в вакууме? Это ток смещения. Можно представить его как круговое движение связанных отрицательных (или наоборот - положительных) зарядов вакуума при полном покое оппозитных зарядов, расположенных

вцентре. Можно представить и как совместное круговое движение положительных и отрицательных связанных зарядов, но с разными скоростями, или по разным радиусам или

вразные стороны… В конечном итоге как бы мы ни рассматривали ситуацию, она будет

сводиться к вращающемуся электрическому полю E , замкнутому в круге. При этом возникает магнитное поле B , связанное с тем, что текут токи и дополнительное, не ограниченное кругом электрическое поле Eинд , связанное с тем, что эти токи ускорены.

Именно это мы и наблюдаем вблизи реальных элементарных зарядов (например, электронов)! Вот наша феноменология так называемого «электростатического» взаимодействия. Не требуется свободных зарядов (с дробными или ещё какими-то величинами заряда), чтобы построить электрон. Достаточно лишь связанных зарядов вакуума! Вспомните, что по современным представлениям фотон также состоит из движущегося электрического поля и в целом электронейтрален. Если фотон «загнуть» кольцом, то у него появится заряд, поскольку его электрическое поле теперь будет двигаться не прямолинейно и равномерно, а ускоренно. Теперь понятно, как образуются заряды разных знаков: если поле E в «кольцевой модели» (рис. 9.1) направлено от центра к периферии частицы, то заряд одного знака, если наоборот – то другого. Если разомкнуть электрон (или позитрон), то создадим фотон. В реальности из-за необходимости сохранения момента вращения, чтобы превратить заряд в фотон, надо взять два противоположных заряда, свести воедино и получить в итоге два электронейтральных фотона. Такое явление (реакция аннигиляции) действительно наблюдается в экспериментах. Так вот что такое заряд – это момент вращения электрического поля! Далее мы попытаемся заняться формулами и расчётами и получить закон Кулона из законов индукции, приложенных к случаю переменного тока смещения.

§ 9.3. Закон Кулона как следствие закона индукции Фарадея

Покажем, что в двумерном (плоском) приближении электрон в электростатическом смысле эквивалентен круговому движению тока, который по величине равен току заряда q0 , движущемуся по радиусу r0 со скоростью, равной скорости света c.

Для этого разобьем полный круговой ток I (рис. 9.1) на элементарные токи Idl , вычислим dEинд , действующие в точке нахождения пробного заряда q , и проинтегрируем по кольцу.

Итак, ток, текущий в нашем случае по кольцу, равен:

(9.1) I = q0v = q0c . 2πr0 2πr0

Поскольку этот ток является криволинейным, то есть ускоренным, то он является

переменным:

179

где a - центростремительное ускорение, которое испытывает каждый элемент тока при движении по окружности со скоростью c .

Подставляя известное из кинематики выражение для ускорения a = c2 , получим: r0

Понятно, что производная для элемента тока будет выражаться формулой:

Как следует из закона Био-Савара-Лапласа, каждый элемент тока Idl создаёт в точке нахождения пробного заряда «элементарное» магнитное поле:

Из главы 4 известно, что переменное магнитное поле элементарного тока порождает электрическое:

Теперь подставим в это выражение значение производной элементарного кругового тока из (9.4):

Остаётся проинтегрировать эти элементарные напряжённости электрического поля по контуру тока, то есть по всем dl , которые мы выделили на окружности:

Нетрудно видеть (рис. 9.1), что интегрирование по углам даст:

Соответственно, полное значение напряжённости электрического поля индукции Eинд от нашего криволинейного тока в точке нахождения пробного заряда будет равно:

180