otvety
.doc|
1.Предмет и основные понятия теории вероятностей. Предметом т.в. явл. Изучение вероятностных закономерностей массовых, однородных, случайных событий.Осн.понятия т.в. явл.опыт-это выполнение комплекса условий в результате кт, происходит или не происходят опр.события. Событие есть возможный результат опыта или испытания и обозначаются(А,В,С…)Достоверным назыв. С. U,кт в данном опыте обязательно произойдет. Невозможным назыв. С. V,кт в данном опыте не может произойти. Случайным назыв.с. А,кт в данном опыте или испытании может произойти,а может и не произойти. |
2.Определение вероятности события. Cв-ва вероятности события. Опр-е- есть колич.мера объективной возможности наступления событий. Cв-ва:1вер-ть с. m=0, P(A)=m/n=0/n=0 2.в-ть достоверного с.=1 m=n,P(V)=1, P(A)=m/n=n/n=1 3.вер-ть случ.с. 0<m<n, 0/n<m/n<n/n, 0<P(A)<1,значит вер-ть любого с. принадлежит промежутку P(A) € [0;1] ; 0≤P(A) ≤1. |
||
|
3.Основные формулы комбинаторики. При
определении вер-ей с. часто используются
ф-лы комб-ки, позволяющие подсчитать
число различных способов выбора k
элементов из n
элементного множества по схеме без
возвращений и с возращениями: чило
размещений из n
элементов по k
элементов без возвращений
|
4.Теоремы сложения и умножения теории вероятностей. Т.сложения вер-ей несовместных с.:Вер-ть суммы двух несовместных с. равна сумме вер-ей этих с.: P(A+B)=P(A)+P(B) Т. Сложения вер-ей совместных с.:Вер-ть суммы двух совместных с. равна вер-ей этих с. без вер-ти их совместного появления: P(A+B)=P(A)+P(B)-P(AB). Т.умножения вер-ей независимых с.:вер-ть совместного появления двух или нескольких независимых с. равна произведению вер-ей этих с.: P(AB)=P(A)*P(B); P(A1A2…An)=P(A2)*…*P(An) Т.умножения вер-ей зависимых с.:Вер-ть произведения двух зависимых с. равна произведению вер-ти наступления первого с на условную вер-ть второго с. при условии,чо первое с. уже наступило P(AB)=P(A)*P(B/A) |
||
|
5.Теорема о наступлении хотя бы одного события и следствие к ней. Вер-ть
наступления хотя бы одного из с.
А1,А2…,Аn,независимых
в совокупности, равна разности м/у
единицей и произведением вер-ей
противоположных с.
|
6.Теорема о полной вероятности и формула гипотез Бейеса. Пусть
с. А может появиться вместе с одним из
попарно несовместных с.
|
||
|
7.Формула Бернулли. Наивероятнейшее число наступления события в независимых испытаниях. Формула Пуассона. Пусть
опыт повторяется в неизменных условиях
n
раз. В каждом опыте некоторое с.А может
наступить с вер-ью p
и не наступить с вер-ью q=1-p.
Вер-ть того,что это с.наступит в n
испытаниях ровно k
раз вычисляестя по ф-ле Бернулли:
Ф.П.
Если вер-ть наступления каждого с. в
независимых испытаниях постоянна и
мала, а число испытаний достаточно
велико, причем npq<10,то
вер-ть того,что в n
независимых испытаниях с. наступит k
раз находится по ф-ле:
Наивероятнейшее
число появления с.А в повторных
независимых испытаниях (k0)определяется
из неравенства:
|
8.Локальная и интегральня формула Лапласа. Л.Если
вер-ть наступления некоторого с. А в
n
независимых испытаниях постоянна,
отлична от нуля и единицы, а число
испытаний достаточно велико, причем
npq<10,то
вер-ть того,что в n
независимых испытаниях с.наступит k
раз находится по ф-ле: И.Если вер-ть наступления с.А в каждом из n независимых испытаний постоянна,отлична от нуля и единицы (0<p<1), а число испытаний достаточно велико, то вер-ть того,что в n испытаниях с. произойдет от k1 до k2 раз, определяется по ф-ле: |
||
|
9.Вероятность отклонения относительной частоты от постоянной вероятности. Вер-ть
того,что в независимых испытаниях
абсолютное отклонение относительной
частоты от постоянной вер-ти не
превзойдет некоторого числа
|
10.Случайные величины и их виды. Дискретная случайная величина. Случ.величиной назыв. Величина,кт в результате опыта может принять то или иное значение, причем до опыта заранее неизвестно,какое именно значение он примет. Случ.величины подразделяются на одномерные и многомерные.Различают дискретные и непрерывные случ.величины. Дискретная случ.величина принимает отдельные, изолированные значения, а непрерывная величина принимает все значения на заданном промежутке. |
||
|
11.Мат. ожидание дискретной случ.величины и его св-ва. Мат.
ожиданием дискретной случ.величины
назыв.сумму произведений всех возможных
значений случ.величины на их вер-ти:
Св-ва :1. Мат.ожид.постоянной величины равно самой постоянной: M(C)=C, 2. Постоянный множитель можно вынести за знак мат.ожидания: M(CX)=CM(X), 3.мат.ожидание суммы 2х или нескольких случайных величин равна сумме их мат.ожиданий: M(X+Y)=M(X)+M(Y), M(∑x1)=∑M(x2), 4. Мат.ожид. произведения 2х или нескольких независимых случ.величин равно произв. их мат.ожиданий M(XY)=M(X)*M(Y) |
12. Действия над случайными величинами. 1. Суммой 2-х СВ Х и У наз-ся случайная величина, которая получается в результате сложения всех значений случайной величины Х и всех значений случайной величины У, а соответствующие вероятности перемножаются. 2. Произведение СВ Х и У наз-ся случайная величина, которая получается в результате перемножения всех значений Х и всех значений У, а соответствующие вероятности перемножаются, |
||
|
13.Дисперсия дискретной случайной величины и ее свойства. Назыв.мат.ожидание квадрата отклонений случайной величины от её мат.ожидания: D(X)=M(X-M(X))2 или D(X)=M(X2 )-M2(X) Св –ва 1.Дисперсия пост.величине равна 0. D(C)=M(C-M(C))2=0, 2.Пост.множитель можно выносить за знак дисперсии возводят его при этом в квадрат: D(CX)=C2D(X), 3. Дисперсия суммы 2х или нескольких случайных величин равно сумме дисперсии этих величин D(X+Y)=D(X)+D(Y) , 4. Дисперсия разности 2х случ.величин равна сумме их дисперсии величин D(X+Y)=D(X+(-1)Y)=D(X)+D(-1Y)=D(X)+(-1)2D(Y)=D(X)+D(Y) |
14.Одинаково распределенные взаимно-независимые случайные величины.
|
||
|
15.Интегральная функция распределения вероятностей и её свойства. Ф-ей
распределения вер-ей случайной величины
Х назыв. ф-ию F(x),
определяющую для каждого значения Х
вер-ть того,что случайная величина Х
примет значение, меньше х, т.е. F(x)=P(X<x)
Св-ва:1.
|
16.Дифференциальная функция распределения вероятностей и её свойства. Дифференциальная
ф-ия или плотность распределения
вер-ей назыв. первую производную от
ф-ции распределения: f(x)=F’(x).Св-ва:1.
f(x)≥0,
2.
|
||
|
17.Числовые характеристики непрерывных случайных величин. 1.
Математическое ожидание. Для НСВ
определяется по формуле:M(X)=
Если
Х определена на интервале (а;b), то
мат.ожидание М(Х)= Св-ва
М(х) и D(х), сформулированные для ДСВ,
справедливы и для НСВ.
5. Среднее
квадратическое отклонение
|
18.Равномерное распределение. Равномерным
назыв.распределение вер-ей непрерывной
случ.величины Х,если на интервале
(а,b),кт
принадлежат все возможные значения
Х, плотность распределения сохраняет
постоянное значение имеет вид: при а<х≤b 1 при х˃b |
||
|
19.Показательное распределение. Показательным назыв. распределение вер-ей непрерывной случ.величины Х,кт описывается полностью. 0 при х<0,
f(x)=
|
20.Нормальное распределение. Норм.
Назыв. распределение вер-ей непрерывной
случайной величины Х, плотность кт
имеет вид
|
||
|
23.Специальные законы распределения. Распределение Стьюдента. Пусть случайная величина X распределена нормально с математическим ожиданием mx и дисперсией σx2, а величина U распределена по закону χ2 с
n степенями
свободы. Тогда величина
будет распределена по закону Стьюдента с n степенями свободы:
Распределение Стьюдента зависит от одного параметра и также приближается к нормальному распределению при неограниченном увеличении n. Этот закон является симметричным относительно начала координат. График плотности распределения (4.17) напоминает график плотности нормального распределения. Распределение Фишера – Снедекора (F-распределение). Пусть случайная величина U распределена по закону χ2 с k степенями свободы, а величина V – по закону χ2 с n степе- нями
свободы. Тогда величина
Снедекора
с k и
n степенями
свободы:
Этот закон распределения вероятностей зависит от двух степеней свободы k и n. |
24.Функция
одного случайного аргумента. Если
каждому возможному значению случайной
величины Х соответствует одно возможное
значение случайной величины У, то У
называют функцией случайного аргумента
Х. У= |
||
|
25.Функция двух случайных аргументов. Если
каждой паре возможных значений
случайных величин Х и У соответствует
одно возможное значение случайной
величины Z,
то Z
называют функцией двух случайных
аргументов Х и У.
|
26.Сущность закона больших чисел. Сущность закона больших чисел состоит в том , что при большом числе независимых опытов частота появления какого-то события близка к его вероятности. ЗАКОН БОЛЬШИХ ЧИСЕЛ – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Первым примером действия этого принципа может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (часто использующееся на практике, например, при использовании частоты встречаемости какого-либо качества респондента в выборке как выборочной оценки соответствующей вероятности).
|
||
|
27Лемма Чебышева. Если
все значения случайной величины Х
неотрицательны , то вероятность того,
что случайная величина Х будет не
меньше некоторого числа t>0
не больше , чем
|
28.Неравенство Чебышева. Если
известна дисперсия случ.величины, то
с её помощью можно оценить вер-ть
отклонения этой величины на заданное
значение от своего мат.ожидания, причем
вер-ти отклонения зависит лишь от
дисперсии.Вер-ть того, что абсолютное
отклонение случ.величины Х от её
мат.ожидания меньше некоторого числа |
||
|
29.Теорема Чебышева. Если
попарно – независимые случайные
величины имеют конечные математические
ожидания, дисперсии каждой из случайной
величины не превосходят постоянного
числа С , то среднее арифметическое
этих величин сходится по вероятности
к среднему арифметическому их
математических ожиданий. Если
|
30) Теорема Бернулли
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р. Возможно определить примерно относительную частоту появления события А.
Теорема. Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико. Здесь т – число появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. . В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании. В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.
Теорема. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна рi, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей рi. Теорема Пуассона
Если
число испытаний n в
схеме независимых испытаний Бернулли
стремится к бесконечности и
Это
означает, что при больших n и
малых p вместо
громоздких вычислений по точной
формуле
На практике пуассоновским приближением пользуются при npq < 9.
|
||
|
32) Задачи математической статистики Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных. Любая наука решает в порядке возрастания сложности и важности следующие задачи: 1) описание явления; 2) анализ и прогноз; 3) поиск оптимального решения. Такого рода задачи решает и математическая статистика: 1) систематизировать полученный статистический материал; 2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины; 3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения. Одной из задач третьего типа является задача проверки правдоподобия гипотез. Она может быть сформулирована следующим образом: имеется совокупность опытных данных, относящихся к одной или нескольким случайным величинам. Необходимо определить, противоречат ли эти данные той или иной гипотезе, например, гипотезе о том, что исследуемая случайная величина распределена по определенному закону, или две случайные величины некоррелированы (т.е. не связаны между собой) и т.д. В результате проверки правдоподобия гипотезы она либо отбрасывается, как противоречащая опытным данным, либо принимается, как приемлемая. Таким образом, математическая статистика помогает экспериментатору лучше разобраться в полученных опытных данных, оценить, значимы или нет определенные наблюденные факты, принять или отбросить те или иные гипотезы о природе рассматриваемого явления. |
33)Предмет и методы математ.стат-ки Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений[1]. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез. Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики предполагают использование возможностей современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости. Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используют точечные и интервальные оценки.
Определим основные понятия математической статистики. Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности. Виды выборки: Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность; Бесповторная – отобранный объект в генеральную совокупность не возвращается.
|
||
|
34)Определение и виды вариационных рядов. графическое изображение Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения.
Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).
Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).
Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.
Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.
Другие формы вариационного ряда - групповые таблицы, составленные по характеру вариации значений изучаемого признака. По характеру вариации различают дискретные (прерывные) и непрерывные признаки.
Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений.
Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.
Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд. |
35)Средняя арифметическая ряда распределения
Средняя
арифметическая применяется, когда
объем совокупности представляет собой
сумму всех индивидуальных значений
варьирующего признака. Следует
отметить, что если вид средней величины
не указывается, подразумевается
средняя арифметическая. Ее логическая
формула имеет вид:
|
||
|
36)Дисперсия ряда распределения и ее свойства.
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий: 1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n - частота (повторяемость фактора Х) Свойства дисперсии 1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится. 2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
|
1. Для первичного ряда:
2. Для вариационного ряда:
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:
где
|
||
|
36)Дисперсия ряда распределения и ее свойства.
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий: 1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n - частота (повторяемость фактора Х) Свойства дисперсии 1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится. 2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
|
1. Для первичного ряда:
2. Для вариационного ряда:
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:
где
|
||

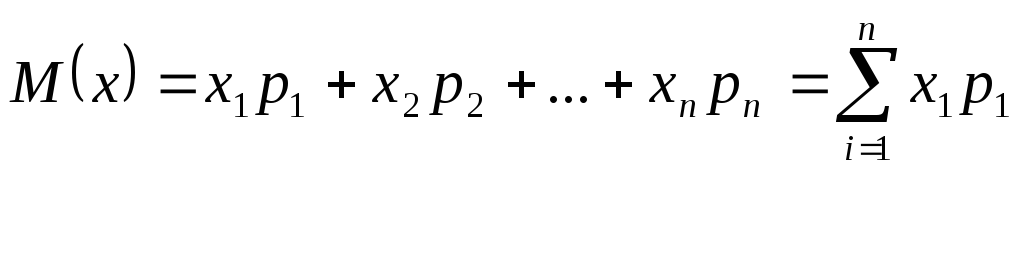
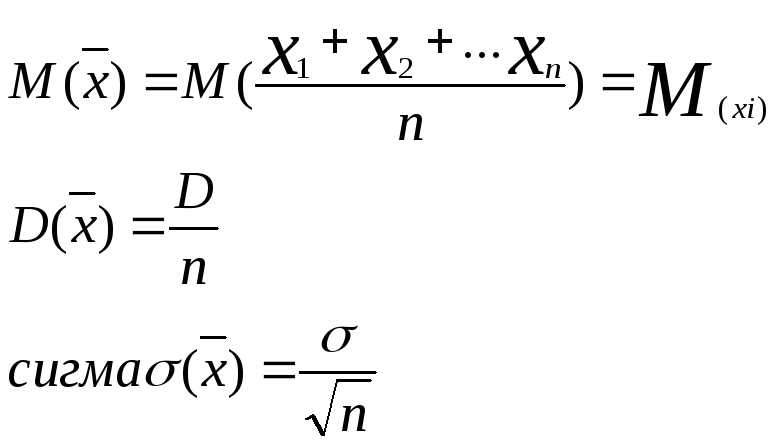
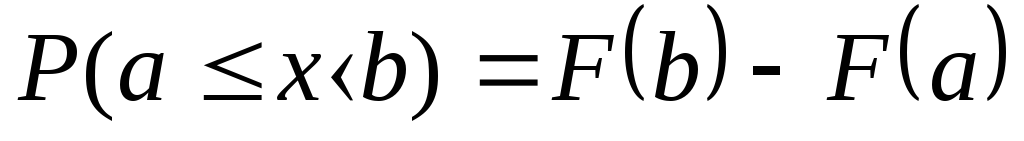
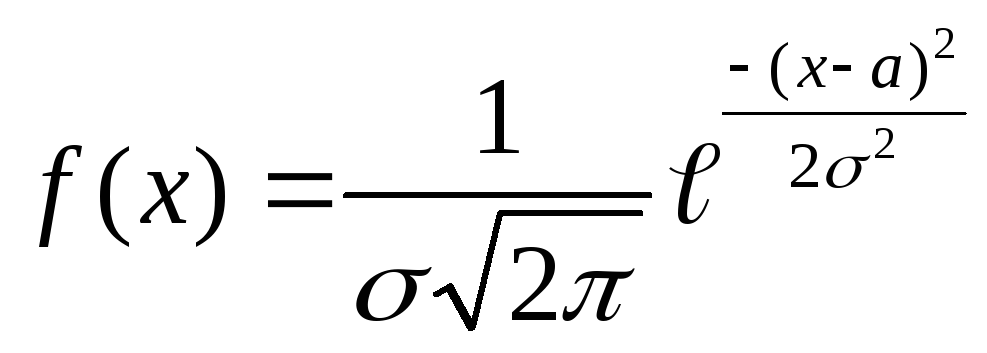 ,
M(x)=a,
D(x)=ơ2
,
M(x)=a,
D(x)=ơ2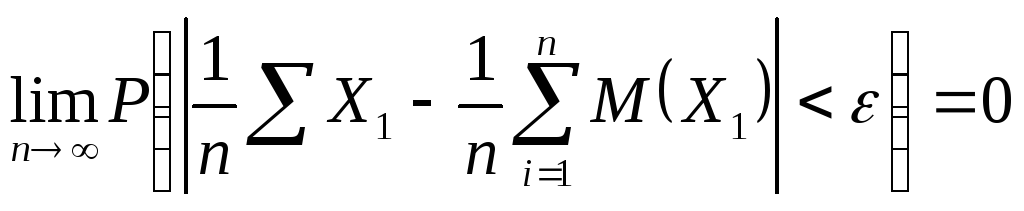 .Воспользовавшись
неравенством , получаем
.Воспользовавшись
неравенством , получаем