Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

jan04075

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

258.86 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

		11
М	етоду	исклю ч ения свойственен характерный недостаток. М оделирую -
щ ий алгоритм описывается ф орм улой ξ =ψ (α1,α2 ,K), где α1 ,α2 ,... - независи-
м ые	БСВ ;	ψ ()× - ф ункция сч етного м нож ества аргум ентов. Последний ф акт

предъявляетж есткие требования к псевдослуч айным ч ислам .

Е сли f0 (x) задана набесконеч ном интервале или не огранич ена, принципиально возм ож но построить м аж орирую щ ую ф ункцию непосредственно. О днако более удобно подобрать преобразование η = φ1(ξ ) так, ч тобы случ айная вели-

ч ина η им ела огранич енную	плотность на конеч ном интервале; η м оделирую т
м етодом исклю ч ения, тогда	= 1−1(ηξ). φ

3.4.М о д ели ро вани енепреры вно й случ айно й вели ч и ны м ето д о м суперпо зи ци и

етодсуперпозиции м оделирования непрерывной случ айной велич ины ξ с

ф иксированной плотностью

распределения f0 (x)

основан на ф орм уле полной

вероятности. Пусть ξ

и ν – случ айные велич ины,

заданные наодном и том

ж е

вероятностном пространстве; Fν (z)- ф ункция распределения ν ;

ξ νp(

z)x- ус-

ловная плотность распределения ξ при условииν = z . Т огдабезусловная плот-

ность распределения ξ равна

0 (

) = ∞ò ξ

ν (

)

ν (z ) . dF

z x

(3.4.1)

−∞

ч астности, если ν – дискретная случ айная велич инасо м нож еством

знач е-

ний { 1, 2 ,K,cN }cивероятностямc

{ {ν

}

ν (:,

,)1= i (x),fi

c x∞≤ p

= =Ni N= i i Pp

то(3.4.1) приним аетвид

0 (

) = å i i (x) f. p f

(3.4.2)

оделирую щ ий алгоритм

i=1

заклю ч ается в следую щ ем :

О пределяется вспом огательная случ айная ν

велич ина так,

ч тобы им ело

м есто(3.4.1) или(3.4.2).

z – реализация ν .

2. М

оделируется ν ; пусть

3. М

оделируется ξ

при условии ν = z ; получ аем

x – реализацию случ айной

велич ины ξ .

Д ля ум еньшения среднего врем ени τ ,

затрач иваем ого на получ ение одной

реализации x , случ айную

велич ину ν

надлеж ит определять так,

ч тобы ν

и ξ

при

ф иксированном

достаточ но

быстро

м оделировались.

Н аибольший

практич еский эф ф ектдаетнепрерывно-дискретный вариант(3.4.2). Граф ич ески

(3.4.2)

означ ает, ч то ф игура единич ной площ ади {(

)

≤

0 ( ),

≤

< c}, x0: b x

разбивается на N непересекаю щ ихся ч астей с площ адям и pi . О сновной прин-

			12
цип разбиения (3.4.2) заклю ч ается			в том ,	ч то	ч асти	gi , им ею щ ие
наибольшую площ адь (наибольшую			вероятность pi ),		долж ны соответствовать
наиболее просто и быстро им итируем ым плотностям					fi (x). О статоч ную плот-
ность	0	( )- å	i i ( )÷ö	6 , 6 = 1- å pi		p p x f p	x f
0 ( ) = çæ	0	( )- å	i i ( )÷ö	6 , 6 = 1- å pi		p p x f p	x f
		5			5
è		i=1	ø		i=1
м ож ноим итировать м етодом		исклю ч ения.

3.5.М о д ели ро вани егауссо вск о й случ айно й вели ч и ны

мето д ам и о братно й ф унк ци и и сум м и ро вани я

Рассм отрим	м оделирование		м етодам и обратной			ф ункции и сум м ирования
гауссовской случ айной велич ины ξ сплотность ю					распределения:
0 (	) 1(	)	( (	)2 (	))μ		Î R1; x μD , (32.D5.1)= - 2 - x =,
						π

где парам етры распределения:μ Î R1 - м атем атич еское ож идание, D - дисперсия.

В ведем в рассм отрение стандартную гауссовскую случ айную велич ину ξ , с плотность ю n1(x 01,). Л егкоубедить ся, ч то

ξ = μ +

(3.5.2)

им еетраспределение (3.5.1). И спользуя соотношение (3.5.2) для м оделирования ξ , обратим ся к задач е м оделированияξ . И сследуем трим етодам оделирования

ξ .

Первый м етодесть ч астный случ ай м етодаобратной ф ункции:

ì	−1	(α ) F		α < , 1<	5,,0
ï						(3.5.3)
ξ = í		−1	( α )	α £ £, 5, 0 1- -0,F
ï
î

где
F( ) = òz	1 (	01,)dx z x n
F( ) = òz	1 (	01,)dx z x n
−∞

есть ф ункция распределения стандартного норм аль ного закона, а F−1(×)– обратная ей ф ункция. В (3.5.3) уч теноизвестное свойство F()× : F(- z) = 1- F(z).

В ыраж ение F−1(z)ч ерез элем ентарные ф ункции отсутствует, поэтом у используется аппроксим ация

−1 (z)

1(z) =Φ

27061θ

, 0

30753

Ψ≈

θ +

−θ

99229

(3.5.4)

04810θ 2 , 0

1 , 0

сошибкой

−1

(z)

1(z )

−3

-< 0,9 или

3 ×10<FприYz

−1 (z)

2 (z)

θ +

01328θ 2

, 0

802853

, 0

- =F

Y»

(3.5.5)

189269

++ 001308θθ + , 0

сошибкой

−1 (z)

1 (z)

×10−44<при5,F

z Y< -0,9 .

В соотношениях(3.5.4), (3.5.5) θ

z < 1.< 5, 0,= 2-ln

В торой

м етод(м етодсум м ирования) основан на центральной предель ной

теорем е. Е слиα1,α2 ,K– независим ые БСВ , топри N → ∞ случ айная велич ина

æ N

N ö

(3.5.6)

N è i=1

2 ø

распределена асим птотич ески норм ально, так ч то ф ункция

распределения

ξ ®Φ

Î 1 . R Fz ), z (

конеч ном

N и определяет м оделирую щ ий

Ф орм ула (3.5.6) при некотором

алгоритм . Случ айная велич ина ξ , определяем ая (3.5.6), аппроксим ирует стан-

дартную

гауссовскую

случ айную

велич ину.

О шибка

аппроксим ации

max

( ) F-(z)

Fтемz Dм еньше=

, ч ем

больше N .

Т ретий м етодявляется м одиф икацией второго. О ч евидно, ч то при пом ощ и специаль ного ф ункционального преобразования из произвольной случ айной велич ины, в ч астности ξ , м ож но получ ить гауссовскую . О днако это преобра-

зование ч ерез элем ентарные ф ункции не выраж ается. Т ем не м енее среди эле- м ентарных ф ункциональ ных преобразований найдены такие, которые сущ ественноум еньшаю т N . В [3] реком ендованоф ункциональ ное преобразование

	41		( 5	3 +15ξ	)-.	ξ10	=ξ	-	ξ ξ

	13440N 2

3.6. М о д ели ро вани егауссо вск о й случ айно й вели ч и ны							м ето д ам и
ф унк ци о нально го прео бразо вани я, и ск люч ени яи суперпо зи ци и
Рассм отрим м оделирование	гауссовской случ айной велич ины ξ с плотно-
стью распределения (3.5.1) с пом ощ ью		м етодов ф ункционального преобразова-
ния, исклю ч ения исуперпозиции.

14
У ч итывая (3.5.2), решим задач у м оделирования	стандартной
гауссовской велич ины ξ . И сследуем двам етодам оделирования ξ .
Первый м етод– м етодф ункционального преобразования -	основан на сле-
дую щ ем утверж дении.
Е слиα1,α2 – независим ые БСВ , тослуч айные велич ины

= -

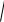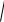(ξ2παcos)

1 2

ξ(2παsin)

2 2

	α2ln
	1	(3.6.1)
	2αln1	(3.6.1)
	2αln1

являю тся независим ым и стандартным и гауссовским и.

оделирую щ ий

алго-

ритм определяется ф орм улой (3.6.1).

В торой м етодисполь зует ком бинацию

м етода суперпозиции с м етодом ис-

клю ч ения.

Представим ξ в виде

ξ =νη ,

(3.6.2)

где ν ,η – независим ые случ айные велич ины; ν -

бернуллиевая случ айная вели-

ч ина, P{ν = − }= P{ν = }1=

5, ;0 η -1 непрерывная случ айная велич инас плотно-

стью

− y2

p, y ³ 0 . e

(3.6.3)

Д ля м оделирования η прим еним

м етодсуперпозиции:

(

) =

(

(y),f

f pp

(3.6.4)

где

1 1

− y2

1 2 ,

1 1

2dy »

6827e

p0,

p= p

= -

(3.6.5)

f1(y) =

− y2 2

[ 01,](ey)

(3.6.6)

f2 (y) =

− y2 2

[1,∞](ey)

Середина распределения

( f1(y)) м оделируется м етодом

исклю ч ения с пря-

м оугольной м аж орирую щ ей ф ункцией

(y) =

[

01,]

(y).

(3.6.7)

тож е

м оделируется

м етодом

«Х вост»

распределения

( f2 (y))

исклю ч ения,

прич ем предварительно используется вспом огательное преобразо-

вание ψ =

(( −η 2 ) 2). Плотн1 остexpь распределения для ψ :

p (z)

−1 2 (

)−1 2

e z ≤ 1=.<

z0,

1−ln (32.6.8)

При м оделировании ψ используем

м етодисклю ч ения с прям оугольной м а-

ж орирую щ ей ф ункцией

(z) =

−1 2

[ 01,](ze).

(3.6.9)

Случ айная велич инаη получ ается обратным преобразованием :

η =

(3.6.10)

− 1lnψ2

Ф орм улы (3.6.2) – (3.6.10) определяю тследую щ ий м оделирую щ ий алгоритм .

1. С пом ощ ью

датч ика БСВ

ф орм ируется псевдослуч айное ч исло α1. Е сли

α1 < 0,5, тореализация s случ айной велич ины ν равнаs = −1, инач е s = 1.

2. Ф орм ируется ч исло α2 . Е сли α2

< p1 , то выч исляется α′ = α2

p1 иосущ е-

ствляется переходк шагу 3 (им итация

f1(y)), в противном случ ае – к шагу 4

(им итация f2 (y)).

(− (α ′)2 2), то реализациexp я y случ ай-

3. Ф орм ируется ч исло α3 . Е сли α3 <

ной велич ины η равна:

y = α′ . В

противном случ ае получ аем

α4 и проверкане-

равенства повторяется,

полагая α′:= α4

и т.д., пока при некоем

αk

не выпол-

нится неравенство. Переходк шагу6.

4. В ыч исляется α′′ = (α

− p ) (1− p1 ). 2

5. Ф орм ируется ч исло αk+1.

Е сли

αk+1 < (

− 1lnα2′′)−1 2 ,

то

реализация

y случ айной велич ины η

равна:

y =

. В

противном

случ ае получ аем

−

1lnα2′′

αk+2 и проверку неравенства повторяем

при α′′:= αk+2 и т.д.,

пока неравенство

не выполнится.

6. В ыч исляется реализация x cлуч айной велич ины ξ : x = sy .

Следуетотм етить , ч то велич ины α

′

′′

позволяю тиспользовать одно ито ж е

,α

псевдослуч айное

ч исло

на различ ных шагах алгоритм а и,

следовательно,

ум еньшаю тврем я м оделирования.

3.7. М

о д ели ро вани еслуч айно й вели ч и ны

с эк спо ненци альны м распред елени ем

Рассм отрим

прим енение м етодов обратной ф ункции, ф ункционального пре-

образования и суперпозиции для м оделирования случ айной велич ины ξ

с экс-

поненциаль ным

распределением

0 (

) = λ −λx , x ³ 0 ,e

(3.7.1)

где λ > 0 – парам етрраспределения.

В ведем

в рассм отрение стандартную

экспоненциальную

случ айную

велич и-

нуξ , сплотность ю

(

) =

− x

³ 0 , x,

(3.7.2)

получ аю щ ейся из (3.7.1) при λ = 1.

Л егкопроверить , ч тослуч айная велич ина

(3.7.3)

ξ = ξ

им еетраспределение (3.7.1).

И споль зуя (3.7.3) прим оделировании ξ ,

обратим ся к задач е м оделирования

ξ . И сследуем

трим етодам оделирования ξ .

Первый м етодесть ч астный случ ай м етодаобратной ф ункции

ξ = −lnα .

(3.7.4).

В торой м етод (м етод ф ункционального преобразования) основан на сле-

дую щ ем утверж дении.

′ K,α , ′ 1;-

Пусть

α α

K α

K,α ,

– ,независим,, ,

ые

БСВ ,

N >

N−1

2N N 1

N−1

велич ины α

N+

,K,α

, расставленные в порядке возрастания;

′

′ =1.

1 N−1

Т огдаслуч айные велич ины

= (

′ -

′ )

(

Kα

) αk =

(3.7.5)

, 1Nαξ

−1

k k

независим ы ираспределены позакону(3.7.2).

Т ретий м етодявляется ч астным случ аем

м етодасуперпозиции и основан на

следую щ ем утверж дении.

Е сли α1,α2 ,K– независим ые БСВ , ν и θ -

не зависящ ие отα1,α2 ,K целоч ис-

ленные полож итель ные случ айные велич ины сраспределениям и

{ν

} (

) −i

{θ

}

((

) )−1

j =i

2,Kj, 1,

e,−,

j!= 1(3=.7P.6) e

тослуч айная велич ина

ξ =ν −

{α1

α2 K,αθ ,}

max

(3.7.7)

им еетплотность (3.7.2). Ф орм ула(3.7.7) определяетм оделирую щ ий алгоритм .

3.8. М о д ели ро вани еслуч айно й вели ч и ны с гам м а- распред елени ем

Д ля м оделирования случ айной велич ины ξ , им ею щ ей гам м а-pаспределение сплотностью

P1e−= ,i=

f0 (x ν )

xν −1e

−x

x ³ 0 ,

(3.8.1)

;

G(ν )

где ν > 0 – парам етр распределения, м огут быть

исполь зованы три основных

м етодам оделирования ξ .

Первый м етод«работает» при целом

ν ³ 1 и используетсвойствобезгранич -

ной делим остизакона(3.8.1). Д ействитель но, характеристич еская ф ункция

∞

−ν

ϕξ ( ;ν )

ò 0 (

itx

dxt e x f

(3.8.2)

(1- it)=

−∞

обладаетсвойством , определяю щ им

безгранич ную

делим ость

(

)−ν m

ξ ( ν )ϕm =m tKt. ϕ , 3, 2ν= it ,= -;

;

ξ (

)

М ож нопоказать , ч то если η1 η2 K,ην ,– независим ые стандартные экспоненциальнораспределенные случ айные велич ины, то

ν
ξ = åη j	(3.8.3)

j=1

им еетплотность (3.8.1).

М оделирование η1 ,K,ην легко осущ ествляется рассм отренным и ранее м етодам и. В ч астности, согласно(3.7.4)

η j	α j j =		, =, - ln	(3.9.5)
		,ν1

где α1 ,K,αν – независим ые БСВ .

О бъединяя (3.8.3) и(3.8.4), получ аем ф орм улу

æ ν ö

ξ= -lnçç∏α j ÷÷ , è j=1 ø

определяю щ ую м оделирую щ ий алгоритм .

В торой м етод прим еним ,

когда ν = N + 05, ;

N =

,0K1, .

У ч итывая (3.8.2),

(3.8.4), представим

характеристич ескую

ф ункцию

случ айной велич ины ξ в ви-

де

(

) ( (

))N (1

1;)−1 2

ϕ (3.8.6)

= ;ç

5, 0- ( )÷ϕ +(t),ϕ= t

η0

j=1

где η0 –случ айная велич инасплотность ю

( )

− z

(

))

η0

z =³ 0 .

,z 05,G

Е ё легко получ ить ф ункциональным

преобразованием стандартной гауссов-

ской велич ины ξ , не зависящ ей отη1,K,ηN :

= ξ

2 .

(3.8.7)

И з (3.8.5), (3.8.6) и(3.8.7) получ аем

ф орм улу

2 ,α

= -

çç

∏ ξ j ÷÷+ ξ*

(3.8.8)

j=1

определяю щ ую

м оделирую щ ий

алгоритм .

оделирование

ξ осущ ествляется

ранее рассм отренным им етодам и.

Н априм ер, согласно(3.6.1)

= -(

N+1

)

2 (2παξcos).

. 2

αln

N+2

Т ретий м етодесть ч астный случ ай м етода исклю ч ения и прим еним для лю -

бого ν.

О бознач им

=ν − [ν ]

≤ν

< 1

и восполь, 0

зуем ся представлением ,

аналогич ным

(3.8.6), (3.8.8):

[ν ]

= -lnçç

∏ ξ j ÷÷ + ξ

j=1

прич ем

pξ совпадаетс (3.8.1), если парам етр приним аетзнач ение ν . Д ля м о-

делирования

ξ ,

прим еним

м етод исклю ч ения

с м аж орирую щ ей

ф ункцией

g(x):

(

)£

ν −1

(x)g=píïxx

,есл и

,01

−x

,есл и

³x . 1

велич инуξ ′ ,

îe

О тм етим :

с плотностью

(

) mesG удобноg x

м оделировать

м етодом

обратной ф ункции:

ì(

[ν ]

)1ν , есл иe

(

+ν

<),0 e

£α1 1

ν α

[ν

]

= í

(

)(ν

−1

−1 ),-

сл уча(е1,

впрот)

ивном

[ν ]+1

′

= g(x)α[ν ]+2 .

2) велич инаη приусловии

= x м оделируется так: η

3.9. М о д ели ро вани еслуч айны х вели ч и н с распред елени ям и χ 2 ,

С тьюд ента, Ф и шера

Рассм отрим

м оделирование случ айной велич ины ξm с χ 2 –распределением с

m степеням исвободы:

−

−x 2

2 1

1( ;fmx) =

x ³ 0 ,

(3.9.1)

2m 2 G(m 2)

случ айной велич ины ηm с t–распределением

Стью дентас m степеням исвобо-

ды:

æ m +1ö

Gç

2 ( ;f my) =

;

(3.9.2)

(

)(

)(m+1) 2

π G

ислуч айной велич ины ςlm с распределением

Ф ишера(l, m - ч исластепеней сво-

боды):

æ l + m ö

−1

l 2

Gç

ml)

3( ; ,mlf) =z

z ³ 0,

(3.9.3)

öæ

lö

(l+m) 2

Gç

÷Gç

÷ç1 +

z ÷

2 ø

è 2

øè

где l, m – натураль ные ч исла– парам етры распределений.

М ож но доказать , ч то, если γ1

γ 2

K,γ m,– независим ые стандартные гауссов-

ские случ айные велич ины, тослуч айная велич ина

ξm = åγ 2j

(3.9.4)

им еетплотность (3.9.1).

j=1

Ф орм ула (3.9.4) и определяетм оделирую щ ий алгоритм

для случ айной вели-

ч ины ξm с χ 2 –распределением

сm степеням исвободы.

А лгоритм для м оделирования случ айной велич ины

ηm с

t–распределением

Сть ю дентас

m степеням и свободы, им ею щ ей плотность (3.9.2), основывается

наследую щ ем

соотношении

m =

ηξm mγ

а ξm -

(3.9.5)

где γ – стандартная гауссовская случ айная велич ина,

не зависящ ая от γ

случ айная велич инасраспределением

(3.9.1).

Д ля м оделирования случ айной велич ины ςlm с распределением Ф ишера(l, m

- ч исластепеней свободы) с плотностью (3.9.3) м ож етбыть использованосоотношение

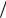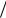= ( l)(ζξm 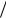m)ξ,l lm (3.9.6)

где ξl ,ξm – независим ые случ айные велич ины с χ 2 –распределениям и(3.9.1).

Зад ани ена вы по лнени елабо рато рны х рабо т по к о м пьютерно м у м о д ели ро вани ю случ айны х вели ч и н

И споль зуя среду автом атизации выч ислений MATHCAD, сф орм ировать выборки знач ений случ айныхвелич инсоследую щ им изаконам ираспределения.

Д ля дискретныхслуч айныхвелич ин: 1.Геом етрич еский законраспределения. 2.Бином инальный законраспределения. 3.Законраспределения Пуассона.

Д ля непрерывныхслуч айныхвелич ин:

1. Закон равном ерной плотности наотрезке [a,b] (используя м етодобратной

функции).

2.Э кспоненциальное распределение (используя м етодобратной ф ункции);

3.Н орм альное (гауссовское) распределение, исполь зуя

а) м етодобратной ф ункции, б) м етодсум м ирования,

в) м етодф ункциональногопреобразования,

г) м етодисклю ч ения исуперпозиции.

4.Гам м а– распределение.

5.Распределение Стью дента.

6.Распределение χ 2.

7.Распределение Ф ишера.

Д ля каж догозаконараспределения сзаданным ипарам етрам ираспределения долж ны быть выполнены следую щ ие задания:

1.Построение при различ ных знач енияхпарам етров граф иков теоретич еской плотности распределения (для непрерывных случ айных велич ин) или вероятности (для дискретных случ айных велич ин) и теоретич еской ф ункции распределения.

2.Ф орм ирование случ айной выборкизаданногообъем а.

3.Построение граф ика выборки (зависим ость выбороч ного знач ения от его ном ера).

4.О пределение основных ч исловых характеристик выборки: выбороч ного среднего, выбороч ной дисперсии, выбороч ного среднеквадратич еского отклонения, м аксим альногоим иним альноговыбороч ныхзнач ений.

5.Построение гистограм м ы и ее сравнение с граф иком теоретич еской плотности распределения (для непрерывных случ айных велич ин) или вероятности (для дискретныхслуч айныхвелич ин).

6.Построение	эм пирич еской ф ункции распределения и ее		сравнение с
теоретич еской ф ункцией распределения.
7. И сследование		зависим ости вида гистограм м ы от объем а выборки (при
ф иксированном	ч исле интервалов разбиения) и отч ислаинтервалов разбиения
(приф иксированном		объем е выборки).
Задания долж ны		быть выполнены для различ ных знач ений	парам етров
распределений.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.05.20151.23 Mб94ISTQB_CTFL_Syllabus_2011_RU.pdf
#
20.05.201553.27 Кб7IS_2.docx
#
21.05.2015602.63 Кб9IZL_-_19_vek.pdf
#
21.05.20151.52 Mб5j.electacta.2013.03.143.pdf
#
19.03.201611.84 Mб211Ja, gerne.pdf
#
21.05.2015258.86 Кб4jan04075.pdf
#
21.05.2015146.06 Кб58Kamalova.L.A.Lekciya_3..Fonetika.pdf
#
19.03.2016308.22 Кб171key-market_leader_book3_2.doc
#
21.05.201523.36 Mб198kholopov-harm-pract1.pdf
#
05.08.2019110.59 Кб2Klassnyy_chas_po_formirovaniyu_pravovoy_kultury....doc
#
20.05.2015277.5 Кб33KlubVer311.doc