Определённый интеграл

Определенный интеграл Римана

Методическое пособие

по дисциплине «Математический анализ»

для студентов 1 курса д/о и в/о, обучающихся по специальностям

010200 «Прикладная математика и информатика»

010500 «Механика»

351400 «Прикладная информатика в юриспруденции»

351500 «Математическое обеспечение и администрирование информационных систем»

Составители:

В.З. Мешков

ВОРОНЕЖ 2003 А.А. Ларин

И.П. Половинкин

В методическом пособии рассмотрены элементы теории определенного интеграла Римана, свойства интегрируемых по Риману функций, признаки интегрируемости функций по Риману, классы интегрируемых функций.

Интегрируемость функции по Риману. Определение интеграла.

Рассмотрим функцию f x , определенную в каждой точке сегмента [a,b]. Введем понятие разбиения сегмента a, b , измельчения разбиения и объединения разбиений.

мельчение разбиения получается добавлением к нему новых точек.

Разбиение называется объединением разбиений и того же сегмен-

где k [xk 1, xk ] .

Отметим, что интегральная сумма Римана зависит как от разбиения , так и от выбора точек k на сегментах [xk 1, xk ] .

Точки k называют промежуточными точками.

Определение. Число Ι называется пределом интегральных сумм Римана

( f , k ) при стремлении мелкости (диаметра) разбиений к нулю, если для

3

если для этой функции на отрезке a, b существует предел Ι ее интегральных

сумм при стремлении диаметра d разбиений к нулю. Число Ι называется

определенным интегралом Римана от функции f x по отрезку a, b и обо-

b

значается f (x)dx .

a

Число a называется нижним пределом интегрирования, число b – верхним пределом. Переменную x под знаком интеграла можно заменить любой другой переменной, так как определенный интеграл – число.

b b b

f (x)dx = f ( y)dy = f (t)dt и т.д.

a a a

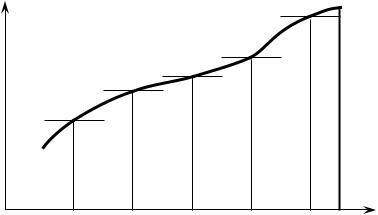
Выясним геометрический смысл интегральной суммы. Рассмотрим криволинейную трапецию, то есть фигуру, ограниченную графиком непрерывной неотрицательной функции f x , заданной на сегменте a, b , двумя прямыми x a, x b , перпендикулярными оси абсцисс и сегментом a, b оси абсцисс. Интегральная сумма ( f , k ) , отвечающая выбранному разбиению и выбо-

y

Определение площади произвольной плоской фигуры мы здесь давать не будем, а примем, что предел при d 0площади указанной ступенчатой фигуры равен площади криволинейной трапеции.

4

Ограниченность интегрируемой по Риману функции.

Теорема. Если функция f x интегрируема по Риману на отрезке a, b , то она ограничена на этом отрезке.

Доказательство. Предположим противное. Пусть функция f x интегрируема на отрезке a, b , но не является ограниченной на нем. Пусть xk mk 0 – произвольное разбиение отрезка a, b . Тогда функция f x будет неограниченной хотя бы на одном отрезке разбиения. Не нарушая общности, можно считать, что f x не ограничена на сегменте [ х0 , x1 ] . На остальных сегментах [ х1, x2 ], …, [ хm 1, xm ] промежуточные точки 2 , 3 , …, m выберем произвольно и зафиксируем. Обозначим через 1 величину

1 f ( 2 ) x2 ... f ( m ) xm .

Рассмотрим теперь функцию f x только на сегменте [ х0 , x1 ]. В силу того, что на этом сегменте функция не является ограниченной, для любого заданного числа M 0 найдется такая точка 1 [x0 , x1 ] , для которой

f ( 1) ( 1 M ) / x1.

Отсюда x1 f ( 1) 1 M , поэтому

m

( f , k ) f ( k ) xk f ( 1) x1 ( 1) f ( 1) x1 1 M .

k 1

Но тогда для разбиения со сколь угодно малым диаметром d и для положительного числа M Ι 1 найдется интегральная сумма ( f , k ) , удовле-

творяющая условию Ι 1, а поэтому Ι Ι 1, что противоречит

существованию предела интегральных сумм, а значит, интегрируемости функции f x . Теорема доказана.

Таким образом, всякая интегрируемая по Риману на отрезке функция ограничена, то есть ограниченность функции, определенной на отрезке, является необходимым условием ее интегрируемости. Обратное утверждение неверно, то есть не всякая ограниченная функция на отрезке интегрируема по Риману на

5

этом отрезке. Другими словами, ограниченность функции на отрезке не является достаточным условием интегрируемости. Для того, чтобы в этом убедиться, рассмотрим в качестве примера ограниченной и неинтегрируемой на отрезке функции функцию Дирихле

Пусть отрезком интегрирования является отрезок 0,1 . Для произвольного разбиения со сколь угодно малым диаметром d , взяв в качестве всех промежуточных точек иррациональные точки, мы получим интегральную сумму 0 , равную нулю, а взяв в качестве всех промежуточных рациональные точки, мы

но это противоречит тому, что 1 0 1. Таким образом, функция Дирихле, будучи ограниченной на отрезке 0,1 , не является интегрируемой по Риману на отрезке 0,1 .

Верхние и нижние суммы Дарбу.

k 1

6

n

s m1 x1 ... mn xn mk xk

k 1

называются соответственно верхней и нижней суммами Дарбу функции f x

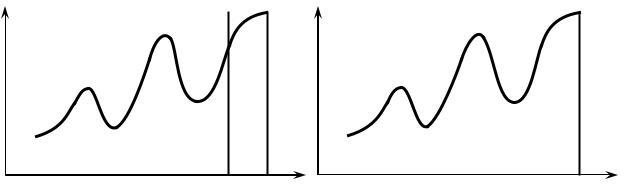
рывной функции является ее максимальным значением на отрезке разбиения [хk 1, xk ] , а число mk - ее минимальным значением на этом отрезке. Поэтому верхняя сумма Дарбу равна площади ступенчатой фигуры, составленной из прямоугольников со сторонами xk и Мk , содержащей криволинейную трапецию, а нижняя сумма Дарбу – площади ступенчатой фигуры, составленной из прямоугольников со сторонами xk и mk , которая содержится в криволиней-

ной трапеции.

Анализируя геометрический смысл интеграла, можно ожидать, что он равен числу, которое следует принять за площадь криволинейной трапеции, а верхняя и нижняя суммы Дарбу являются приближениями этой площади с избытком и недостатком соответственно.

Свойства сумм Дарбу.

Лемма 1 (об оценках интегральных сумм Римана).

Пусть ( f , k ) – интегральная сумма, отвечающая данному разбиению

xk nk 0 . Тогда при любом выборе промежуточных точек k всегда справедливы неравенства

7

s S ,

где s , S – соответственно нижняя и верхняя суммы, отвечающие тому же разбиению.

Доказательство. По определению чисел mk , M k заключаем, что для лю-

бого k xk 1, xk

m f ( k ) M k , k=1, …, n

Умножая эти неравенства на xk , суммируя по k, получаем требуемое утверждение. Лемма доказана.

Лемма 2 (о приближении сумм Дарбу суммами Римана).

Пусть xk nk 0 – произвольное фиксированное разбиение сегмента a, b ,- произвольное положительное число. Тогда можно выбрать промежуточные точки k таким образом, чтобы интегральная сумма ( f , k ) и верхняя сумма

ждение. Второе доказывается аналогично. Лемма доказана.

Следствие. Для любого фиксированного разбиения xk nk 0 справедливы соотношения

где sup и inf берутся по всевозможным наборам промежуточных точек.

Лемма 3 (о монотонности сумм Дарбу).

При измельчении данного разбиения верхняя сумма Дарбу не увеличивается, а нижняя сумма Дарбу не уменьшается, то есть если – измельчение разбиения , то S S , s s .

Доказательство. Доказательство достаточно ограничить случаем, когда разбиение получается из разбиения добавлением одной новой точки x .

8

Пусть x xk 1, xk . Тогда в выражении для S слагаемое M k xk надо заме-

Точная верхняя грань функции на части сегмента не превосходит точной

верхней грани функции на всем сегменте, поэтому M k Mk , M k M k . Отсюда

M k (x xk 1) M k (xk x) Mk (x xk 1) (xk x) Mk xk ,

так как все другие слагаемые в выражении для верхней сумм S такие же, как и для суммы S . Поэтому мы доказали, что при измельчении разбиения верхние суммы Дарбу могут только уменьшаться. Аналогично показывается, что при измельчении разбиения нижние суммы Дарбу могут только увеличиваться.

Лемма доказана.

Лемма 4 (о неравенстве для верхних и нижних сумм Дарбу)

Для двух произвольных различных разбиений сегмента a, b нижняя сумма одного из разбиений не превосходит верхней суммы другого разбиения.

Доказательство. Пусть и - два произвольных разбиения сегментаa, b , S , s , S , s – верхние и нижние суммы этих разбиений соответственно.

Обозначим через объединение разбиений и , а через S , s соответственно верхнюю и нижнюю суммы Дарбу разбиения . Разбиение является измельчением как разбиения , так и разбиения . Согласно лемме 3 о монотонности сумм Дарбу имеем

S S , S S , s s s s .

Кроме того s S , так что

s s S S s S s s S S s S .

Лемма доказана.

Следствие (свойство ограниченности сумм Дарбу)

Множество всех верхних сумм Дарбу ограниченной функции f x , отвечающих всевозможным разбиениям сегмента a, b , ограничено снизу. Множество нижних сумм Дарбу ограничено сверху.

Действительно, любая верхняя сумма не меньше некоторой фиксированной нижней суммы, следовательно, множество верхних сумм ограниченно снизу. Множество нижних сумм аналогично ограничено сверху.

9

Верхний и нижний интегралы Дарбу. Основная лемма Дарбу.

Мы выяснили, что множество всех верхних сумм ограниченной функции, отвечающих различным разбиениям отрезка a, b , ограничено снизу. Поэтому оно имеет точную нижнюю грань. Множество всех нижних сумм Дарбу ограничено сверху, поэтому оно имеет точную верхнюю грань.

Определение. Точная нижняя грань множества всех верхних сумм Дарбу функции f x , отвечающих различным разбиениям отрезка a,b , называется

суммы Дарбу для разбиения , а S , s – верхняя и нижняя суммы Дарбу разбиения .

Лемма. Для разностей S S s s выполняются следующие неравенства

S S (M m)ld , s s (M m)ld .

10

менится двумя слагаемыми

S S M xk m[( x xk 1) (xk x)] (M m) xk (M m)d .

Если теперь разбиение получается из разбиения добавлением еще одной точки, то, по доказанному, получаем

S S (M m)d

Откуда

S S (M m)d , S S S S S S 2(M m)d и т.д.

Аналогично доказывается неравенство для нижних сумм. Лемма доказана. Определение. Число A называется пределом верхних сумм Дарбу S при

стремлении к нулю диаметра разбиений d, если для любого положительного

Аналогично определяется предел B нижних сумм s при стремлении d к нулю.

Лемма (основная лемма Дарбу). Верхний интеграл Дарбу Ι * является пределом верхних сумм S при стремлении d (диаметра разбиений) к нулю, то есть

11