Нов.ПМС-2

0 из модели возможно с помощью «центрирования» данных,

так как x y 0 при любом значении b1 .

Поэтому можно записать центрированную модель, совсем опуская свободный член (отрезок)

Таким образом, мы потеряли один параметр, что соответствует потере данных, а это влечет за собой потерю части информации. Потерянная часть информации эффективно используется для корректировки модели, позволяющей исключить свободный член

9.4. Точность оценки регрессии

Рассмотрим вопрос о том, какая точность может быть приписана оценке линии регрессии. Рассмотрим тождество:

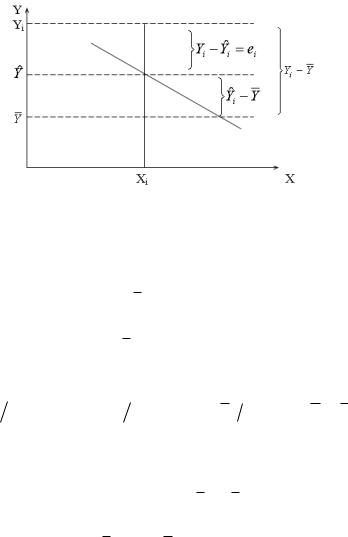
Что это означает геометрически, показано на рис. 9.3.

Рис. 9.3

Остаток ei Yi Yi представляет собой разность между двумя величинами:

1) отклонением наблюдаемого значения отклика Yi от

общего среднего откликов Y и

2) отклонение предсказанного значения отклика Yi от

того же общего среднего Y .

Заметим, что среднее арифметическое предсказанных значений Yi равно

Иными словами, среднее арифметическое предсказанных

Если мы возведем обе части этого выражения в квадрат и

В уравнении (9.21) величина Yi Y – это отклонение i -го

наблюдения от общего среднего, следовательно, левая часть уравнения (9.21) – это сумма квадратов отклонений

наблюдения от его предсказанного или вычисленного значения

( i -й остаток), а Yi Yi – отклонение предсказанного значения

i -го наблюдения от среднего, то мы можем выразить уравнение (9.21) словесно следующим образом: «сумма квадратов относительно среднего» = «сумма квадратов относительно регрессии» + «сумма квадратов, обусловленная регрессией».

Пригодность линии регрессии для целей предсказания зависит

R2 SS, обусловлен ная 1.

SS, относительна

будет не слишком отличаться от 1.

Всякая сумма квадратов связана с числом, называемым ее степенями свободы. В статистике числом степеней свободы некоторой величины часто называют разность между числом различных опытов и числом констант, найденных по этим опытам независимо друг от друга.

Это понятие можно применить к сумме квадратов. Мы получим число, которое показывает, как много независимых элементов информации, получающихся из n независимых чисел Y1 ,...Yn , требуется для образования данной суммы

квадратов. Например, для SS относительно среднего

103

степени свободы. Это отражает тот факт, что рассматриваемые остатки получены для модели прямой линии, которая требует оценивания двух параметров. Вообще, остаточная сумма квадратов основывается на числе степеней свободы, равном числу наблюдений минус число оцениваемых параметров. Следовательно, в соответствии с уравнением (9.21) мы можем разложить степени свободы таким образом:

. (9.22)

Пользуясь уравнениями (9.21) и (9.22), мы можем построить таблицу дисперсионного анализа. (ANOVA). Обозначение ANOVA произошло от английских слов « Analysis of variance». «Средний квадрат» MS получается при делении каждой суммы квадратов SS на соответствующее ей число степеней свободы.

Таблица 9.1. Таблица дисперсионного анализа (ANOVA). Основное

разложение

Продолжение табл. 9.1

Более общая форма таблицы дисперсионного анализа получается при добавлении в таблицу корректирующего фактора для среднего Y -в, который называется SS(b0 ) .Это

название будет пояснено позже

Таблица 9.2 Таблица дисперсионного анализа (ANOVA), включающая

SS(b0 )

105

Сумма SS редко подсчитывается так, как показано в таблице, а обычно получается делением SS(b1 b0 ) на общую

скорректированную SS . Сумму квадратов, обусловленную регрессией, можно вычислять множеством способов (суммирование везде идет по i 1,2,...n ):

Уравнение (9.23) проще всего использовать, поскольку оба сомножителя уже получены при подборе уравнения прямой. Округление может внести неточности, лучше использовать формулу (9.24), где деление производится в

106

последний момент.

Общую скорректированную сумму квадратов можно записать и вычислить следующим образом:

SYY (Yi Y )2 = Yi 2 ( Yi )2 n = .

относительно регрессии, основанную на (n-2) степенях свободы. Будем обозначать эту величину YX2 . Если уравнение

регрессии будет оцениваться из большого числа наблюдений, то дисперсия относительно регрессии будет представлять ошибку измерения, с которой любое измеренное Y предсказывается для данного значения X по известному уравнению:

Исследуем уравнение регрессии. Пока не были использованы предположения о распределении вероятностей. Теперь введем основные предположения о том, что в модели

независимыми

Замечание 1.

Дисперсия 2 может быть равной или не равной YX2 – дисперсии относительно регрессии. Если постулированная модель не соответствует «истинной», то 2 YX2 . Из этого следует, что s 2 – остаточный средний квадрат, который в любом случае оценивает YX2 – служит оценкой 2 , если только модель корректна. Если 2 YX2 , то постулируемая

модель некорректна или страдает неадекватностью.

Замечание 2.

Во многих реальных ситуациях ошибки, в соответствии с центральной предельной теоремой, подчиняются нормальному распределению. Если оказывается суммой ошибок, то, независимо от того, как распределены отдельные ошибки, их сумма имеет тенденцию к нормальному распределению в соответствии с центральной предельной теоремой.

( X1 X )Y1 ... ( X n X )Yn .( X i X )2

Далее, дисперсия некоторой функции

F a1Y1 ...anYn

равна

D(F) a12 D(Y1 ) ... an2 D(Yn ) ,

если Yi попарно некоррелированы и ai – константы.

108

Если неизвестна и мы используем вместо нее оценку s , предполагая, что модель корректна, то оценка стандартного отклонения b1 есть

Вместо термина «оцениваемое стандартное отклонение» обычно используют термин «стандартная ошибка». Если мы предполагаем, что разброс наблюдений относительно линии

Стьюдента с n 2 степенями свободы.

109

Сдругой стороны, мы можем проверить нуль - гипотезу

отом, что 1 10 ,

где 10 – частное значение, которое может быть нулем против

степенями свободы – числом, на котором основана оценка s 2

проверки гипотезы с помощью t -критерия. Достаточно

110