
kostrub_lab_method
.pdf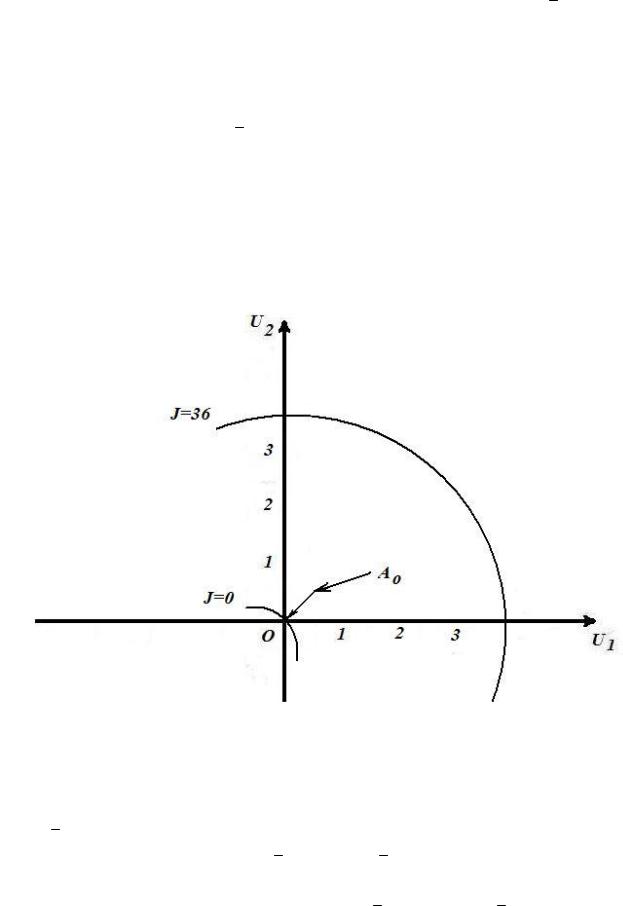
Чем ближе к минимуму при r 0 , тем меньше градиент функции P(u, r) .
Поиск заканчивается, если rk , где – малая положительная величина.
Графическая иллюстрация примера показана на рис. 6.
Линии уровня функции J (u ) u12 6u1 u22 9u2 есть концентрические окружности с центром в точке с координатами (u1 , u2 ) ( 3; 9 / 2) .
(u1 3)2 |
(u2 |
9 / 2)2 |
117 / 4, |
если |
J 0 , |
(u1 3)2 |
(u2 |
9 / 2)2 |
121/ 4, |
если |
J 1 |
и так далее.
Рис. 6
АЛГОРИТМ
Шаг 1. Задать 0 - требуемую точность. Задать координаты исходной точки u . Положить k 0, rk 1.
Шаг 2. Найти минимум функцииP(u, rk ) в точке u * k . Проверить критерий остановки метода rk . Если он выполнен, то вычисления завершаются. Точка минимума найдена u * k . Считаем J (u * ) .
21

Шаг 3. Положить k k 1, rk rk 1 / C . Принять за новую начальную точку u u * k 1 . Перейти к шагу 2.
Замечание. Использование штрафных функций для решения задач связано с определенной вычислительной трудностью. Прежде всего поиск может начинаться с допустимой точки u , для которой gi (u1 ,..., un ) 0, i 1,2,..., m.
Для некоторых задач находить такую точку довольно сложно. Кроме того, вследствие использования в алгоритме оптимизации дискретных шагов около границы {u : gi (u1 ,..., un ) 0} возможен шаг, который выводит за границы
допустимой области. Он приводит к уменьшению значений функции P(u, rk ) ,
т.е. к фиктивному успеху. Таким образом, нужна явная проверка допустимости каждой последующей точки, для чего на каждой итерации необходимо вычислять значения функции gi (uk ), k 1,2,... .
МЕТОД БАРЬЕРНЫХ ФУНКЦИЙ
Метод штрафных функций относится к группе методов внутренней точки, т.е. он начинает работать с допустимой точки u0 и генерирует
последовательность допустимых точек u1 ,u2 ,...,un . Метод барьерных функций,
наоборот, относится к группе методов внешней точки, он начинает поиск с недопустимой точки и генерирует последовательность недопустимых решений, которая приближается к оптимальному решению извне допустимой области.
Постановка задачи. Требуется найти минимум функции J (u1 ,...,un ) при ограничениях gi (u1 ,...,un ) 0, i 1,2,..., m , hi (u1 ,...,un ) 0, i m 1, ,...,l или
J (u1 ,..., un ) inf,
gi (u1 ,..., un ) 0, i 1,2,..., m , hi (u1 ,...,un ) 0, i m 1, ,...,l .
В частности, для искомых функций – ограничений целесообразно использовать барьерную функцию следующего вида
m |
l |
(u) R1 (gi (u)) |
R2 (hi (u)) , |
i 1 |
i m 1 |
где R1 , R2 - непрерывные функции, которые удовлетворяют условиям
R1 (v) 0 , если v 0 и R1 (v) 0 , если v 0 , R2 (v) 0 , если v 0 и R2(v) 0 , если v 0 .
22
Типичными являются следующие выражения для функций R1 , R2
R1 (v) (max{0, v}) p , |
R2 (v) | v | p , |
где p - целое положительное число. |
|
Далее от исходной задачи переходим к задаче безусловной оптимизации вспомогательной функции. Минимизировать J (u) r (u) , где r 0 - штрафной
коэффициент.
Пусть – непрерывная функция. Обозначим (r) inf {J (u) r (u)} .
Подход, связанный с барьерной функцией состоит в решении задачи вида максимизировать (r) при ограничении r 0 .
АЛГОРИТМ
Шаг 0. Выбрать 0 . Выбрать начальную точку u1 , параметр штрафа r0 и число 1 . Положить k 1 и перейти к основному этапу.
Основной этап ( k -я итерация).
Шаг 1. При начальной точке uk и параметре штрафа rk решить следующую задачу: минимизировать функцию
m |
l |
J (u) rk (u) J (u) rk { (max{0, gi (u)}) p |
|hi (u) | p , |
i 1 |
i m 1 |
где p - целое положительное число.
Положить uk 1 равным оптимальному решению задачи и перейти к
шагу 2. |
|
Шаг 2. Если rk (uk 1 ) , то вычисления завершить. Иначе положить |
rk 1 rk , |
k k 1. Перейти к шагу 1. |
|
Замечание. На эффективность метода барьерных функций существенно влияют выбор начального значения r0 и метод сокращения значений в процессе
минимизации, а также выбор весовых коэффициентов wi . Если в функции значение P(u, r) , выбирают слишком малым, то уже на начальной стадии процесса приходят к минимуму функции J (u) , который вряд ли окажется вблизи действительного условного минимума в точке u* . С другой стороны, если значение r0 , выбирается слишком большим, то на первых итерациях
23
вычислительного процесса текущая точка неизбежно окажется слишком далеко за пределами допустимой области, и поиск из-за необходимости возврата в пределы допустимой области окажется весьма затяжным.
Задания. 1. Показать, что для метода наискорейшего градиентного спуска, применённого к функции J (u1 ,u2 ) u12 u2 2 , 0 , выполнение одной итерации из точки (u1k ,u2k ) ( , / ) приводит к уменьшению значения функции
по закону |
J k 1 J k q( ) , где q( ) 1 |
|
(1 2 / 2 )2 |
|
. |
|
(1 |
3 / 2 )(1 / 2 ) |
|||||
|
|
|
||||
Исследовать зависимость q от параметра |
размещения точки начала |
|||||
итерации. Какая связь J k 1 с J k будет в случае использования метода Ньютона?
2. Для функции J (u1 , u2 ) 4(u1 u2 )2 (u1 |
u2 )2 построить множество точек, |
|||||
в которых выполняется критерий останова || |
grad J (u1 , u2 ) || при 1. |
|
||||
3. Для функции J (u1 ,u2 ) u1 |
2 u2 |
2 , 0 применить метод наискорейшего |
||||
спуска, метод Ньютона из начальной точки |
u0 (u10 , u20 ) ( , / ) |
построив |
uk |
|||
для k 1,2 . Сколько итераций |
потребуется |
этим методам для |
попадания |
в |
||
минимум функции J ?
4. Решить задачу многомерной минимизации
J (u) inf .
Помимо точек минимума посчитать число итераций и сделать вывод о целесообразности использования каждого из методов в той или иной ситуации. Использовать методы: а) дробления шагом; б) наискорейшего спуска; в) Ньютона; г) штрафных функций. В двух последних методах ограничения брать из приведённых выше примеров. Решение поставленной задачи оформить в виде отчёта.
1. J (u) 3u1 2u2 u12 2u22 . 3. J (u) u12 u22 2u1 8u2 . 5. J (u) 9(u1 5)2 4(u2 6)2 . 7. J (u) (u1 3)2 (u2 4)2 . 9. J (u) u1 3u2 u12 2u22 . 11. J (u) (u1 u2 )2 u1 u2 . 13. J (u) (u1 4)2 (u2 3)2 . 15. J (u) (2u1 u2 )2 u1 u2 . 17. J (u) (u1 3)2 (u2 5)2 . 19. J (u) (u1 5)2 (u2 3)2 . 21. J (u) 3u1 4u2 u12 u22 .
2.J (u) 3u12 4u1u2 3u22 .
4.J (u) 4u1u2 5u12 u22 .
6.J (u) u12 u22 .
8.J (u) 6u1u2 u12 u22 .
10.J (u) 4u1u2 u12 u22 . 12. J (u) 3u1u2 u12 u22 .
14.J (u) 5u1u2 3u12 4u22 . 16. J (u) 3u1u2 u12 u22 . 18. J (u) u1u2 u12 u22 .
20. J (u) (u1 u2 )2 2u1 3u2 22. J (u) 3u1u2 u12 u22 .
24

23. J (u) (u1 |
u2 )2 |
9u1u2 . |
|
|
|
|
|
|
24. J (u) 4u1u2 2u12 |
3u22 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
25. J (u) (u1 |
u2 )2 u1 |
5u2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАЧА ПРОДАВЦА ГАЗЕТ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Рассмотрим конкретный пример. Пусть i - номер дня. Нас интересует |
||||||||||||||||||||||||||||||||||||||||||||||
q |
- размер |
партии |
|
|
заказа. |
Известно h 2 - |
издержки |
хранения; |
|
d 4 - |
||||||||||||||||||||||||||||||||||||||
издержки дефицита; |
ri - |
столько газет куплено (для непрерывной задачи |
||||||||||||||||||||||||||||||||||||||||||||||
пишем r вместо ri |
); Pi - вероятность продажи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Ряд распределения запрашиваемых газет выглядит так |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ri |
|
0 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
4 |
|
|
|
5 |
|
|
6 |
|
|
|
7 |
|
|
|
|
|
8 |
|
|
9 |
|
|
|
10 |
||||
Pi |
|
0,1 |
|
|
|
0,05 |
|
|
0,15 |
|
|
|
0,1 |
|
0,05 |
|
|
0,1 |
|
0,1 |
|
|
0,1 |
|
|
|
0,15 |
|
0,1 |
|
|
0 |
||||||||||||||||
|
|
Интересующая нас величина q - оптимальная партия. Чтобы ее |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
посчитать, нужно знать характеристическое соотношение затрат |
|
d |
|
|
|
ˆ |
||||||||||||||||||||||||||||||||||||||||||
h d |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
L(q) . |
|||||||||||||||||||||||||||||||||||||||||||||||
Учтем, что |
L(q |
|
1) |
|
|
|
h |
d |
|
|
|
|
L(q) , где |
L(q) |
|
q |
|
|
|
P |
)(q |
|
1) . Посчитаем |
|
|
|||||||||||||||||||||||
|
|
|
|
d |
|
|
|
Pi |
|
|
( r |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
i q 1 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
величину |
|
|
4 / 6 0,667 |
и заполним таблицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
h |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi (q 1) |
|
|
|||||||||||||||
q |
|
ri |
|
|
|
Pi |
|
|
|
|
|
|
|
|
|
|
Pi |
|
|
|
|
|
|
Pi |
|
|
|
|
|
|
|
L(q) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
i q 1 |
ri |
|
|
|
|
|
|
|
i q 1 |
ri |
|
|
|
|
|
|
|
|
||||||
0 |
|
0 |
|
0,1 |
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
0,25 |
|
|
|
|
|
|
|
|
|
0,125 |
|
|
|
|
0,225 |
||||||||||||||
1 |
|
1 |
|
0,05 |
|
|
|
|
|
|
0,15 |
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
0,45 |
|||||||||||||
2 |
|
2 |
|
0,15 |
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
0,12 |
|
|
|
|
|
|
|
|
|
0,31 |
|
|
|
|
0,615 |
|||||||||||||||
3 |
|
3 |
|
0,1 |
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
0,09 |
|
|
|
|
|
|
|
|
|
0,34 |
|
|
|
|
0,71 |
||||||||||||||
4 |
|
4 |
|
0,05 |
|
|
|
|
|
|
0,45 |
|
|
|
|
|
0,08 |
|
|
|
|
|
|
|
|
|
0,36 |
|
|
|
|
0,81 |
||||||||||||||||
5 |
|
5 |
|
0,1 |
|
|
|
|
|
|
|
0,55 |
|
|
|
|
|
0,06 |
|
|
|
|
|
|
|
|
|
0,33 |
|
|
|
|
|
|
|
|
||||||||||||
6 |
|
6 |
|
0,1 |
|
|
|
|
|
|
|
0,65 |
|
|
|
|
|
0,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7 |
|
7 |
|
0,1 |
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
0,03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8 |
|
8 |
|
0,15 |
|
|
|
|
|
|
0,9 |
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9 |
|
9 |
|
0,1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Как видно из таблицы наше q |
|
3 , т.е. оптимальная партия газет 3 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
штуки.
Задание. Написать программу, реализующую данный алгоритм. Сделать подробные комментарии и инструкцию пользователя. Необходимые величины взять произвольными и для них определить оптимальный размер партии заказа.
25

ЗАДАЧА УПРАВЛЕНИЯ ЗАПАСАМИ
Постановка задачи. Имеется база, на которой хранится некоторый запас некоторого продукта. Этот продукт выдается непрерывно, система должна работать бесконечно. Определить размер партии заказа и интервалы между поступлениями, минимизирующие суммарные издержки.
Система работает без дефицита d . Постоянные издержки s . Поступление продукта в ситему мгновенно p . Скорость выдачи продукта
r . Затраты на хранение единицы продукта в первый период h0 . Это все
постоянные величины.
Длина периода T . Размер партии заказа в i -й период qi . Затраты на хранение единицы продукта в i -м периоде hi .
Суммарная величина издержек C(q) |
1 |
hqT |
|
|
hq |
|
sr |
. |
||
|
|
|
s |
|
|
|
|
|||
T |
2 |
2 |
q |
|||||||
|
|
|
|
|
|
|||||
Надо определить оптимальный размер партии заказа qˆ , который минимизирует суммарные издержки.
АЛГОРИТМ
Шаг 1. Отрезок 0,T разбиваем на n частей: i 0,1,..., n .
Шаг 2. Если qi 1 q qi (i 0,1,..., n) , то hi (q) h0 i , причем hi (q) 0 .
Шаг 3. Ищем C (q) h2 qsr2 0 , откуда qˆ (2sr / h)1/ 2 .
Задание. Написать программу, реализующую данный алгоритм. Сделать подробные комментарии и инструкцию пользователя. Необходимые величины взять произвольными и определить оптимальный размер партии заказа qˆ , минимизирующий суммарные издержки.
|
|
ЗАДАЧА ТЕОРИИ РАСПИСАНИЙ |
|
|
||
Постановка |
задачи. Имеется m ( j 1,..., m) работающих |
станков и |
||||
n (i 1,..., n) |
деталей, которые |
последовательно |
обрабатываются |
на них. |
||
Известно |
время |
обработки |
i -й детали на |
j -м станке |
( tij ). |
Найти |
последовательность запуска деталей на станки, чтобы производственный цикл был минимальным.
АЛГОРИТМ
( m 2 )
Пусть ai - время обработки i -й детали на 1-м станке; bi - время
обработки i -й детали на 2-м станке. Строим график Ганта для исходной последовательности. Искомая нами последовательность j -я.
26
Шаг 1. Рассматривается вся таблица. Ищется минимальный элемент во всей таблице.
Если он принадлежит порядку обрабатываемых деталей на 1-м станке (в графе ai ), то эта деталь имеет номер N 1.
Если это элемент из графы bi , то эта деталь получает последний номер. Если ai bi , то не играет роли, какой номер первый, а какой последний.
Если минимальный элемент неединственный, то выбираем любой из них.
Далее рассматриваемая строка вычеркивается.
Шаг 2. Повторяем пункт 1 до тех пор, пока не будут вычеркнуты все строки. Шаг 3. Строим график Ганта для новой последовательности.
ПРИМЕР
Пусть ai - время обработки i -й детали на 1-м станке; bi - время
обработки i -й детали на 2-м станке. Найти последовательность обработки деталей, чтобы длина производственного цикла была минимальной. Данные приведены в таблице, n 6, m 2 .
i |
1 |
2 |
3 |
4 |
5 |
6 |
ai |
2 |
6 |
8 |
4 |
4 |
2 |
bi |
5 |
1 |
3 |
4 |
7 |
4 |
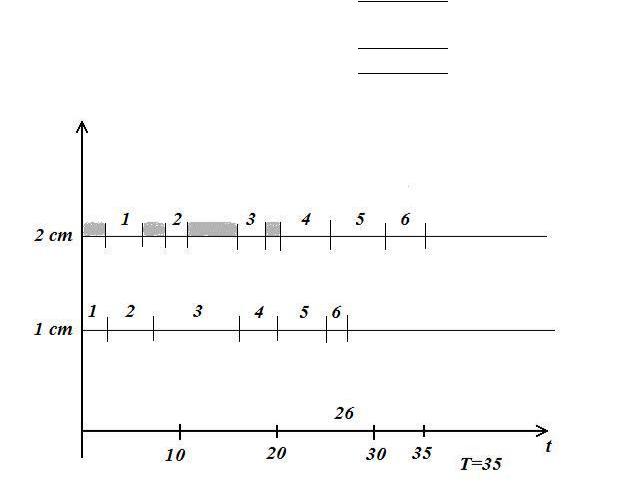
Рис. 7
27
Построим график Ганта для этой последовательности (см. рис. 7). Минимальный цикл 35 единиц.
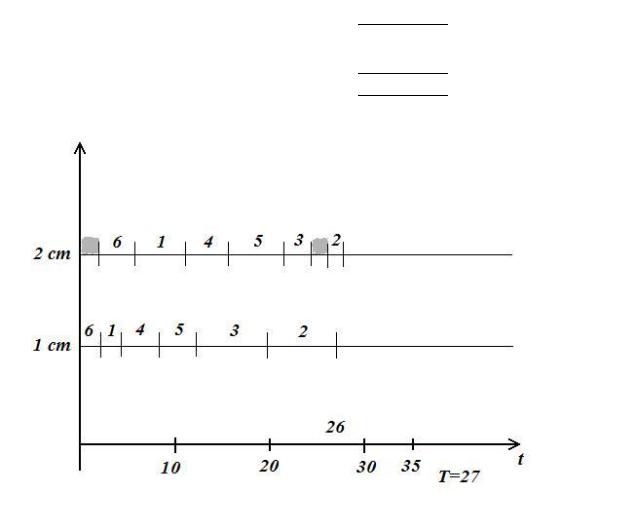
Строим новую последовательность по приведенному алгоритму и новый график (см. рис. 8). Как видим, новый минимальный цикл 27 единиц.
i |
1 |
2 |
3 |
4 |
5 |
6 |
ai |
2 |
6 |
8 |
4 |
4 |
2 |
bi |
5 |
1 |
3 |
4 |
7 |
4 |
j |
2 |
6 |
5 |
3 |
4 |
1 |
Рис. 8
Задание. Написать программу, реализующую данный алгоритм. Сделать подробные комментарии и инструкцию пользователя. Необходимые величины взять произвольными.
ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Постановка задачи. Имеется несколько мест обслуживания (приборы); известны характеристики (среднее количество обслуживания в единицу времени); существует очередь желающих получить данное обслуживание (элементы стоящие в очереди – это заявки). Найти оптимальные условия функционирования систем.
28

Считаем основные характеристики
Среднее число поступления заявок в очередь в единицу времени . Среднее число заявок обслуживаемых приборов в единицу времени .
Интенсивность обслуживания . Для эффективности !
Среднее количество заявок в системе n . Среднее количество заявок в очереди .
Среднее время пребывания заявки в системе. Оно равно среднему времени пребывания заявки в очереди t .
S - число приборов в системе.
Если n S , то все заявки обслуживаются; число свободных приборов S n ; среднее число обслуживаемых n .
Если n S , то все приборы заняты; число заявок в очереди n S ; среднее число обслуживаемых S .
ПРИМЕР
Бензоколонка работает 6 часов без перерыва. В среднем в день заправляется 54 машины. Время обслуживания любой машины 5 минут. Определить основные характеристики системы.
|
|
|
|
Посчитаем |
основные характеристики: 54 / 6 9 машин |
в час; |
||||||
60 |
мин/(5 мин/ маш) 12 машин в час; |
/ 9 /12 0,75 1, |
т.е. |
работа |
||||||||
бензоколонки |
эффективна; |
n /(1 ) 0,75 /(1 0,75) |
3 машины; |
|||||||||
|
2 |
/(1 ) 0,5625 /(0,25) 2,25 машин; |
|
/( (1 )) . |
|
|
||||||
|
|
|
|
|
/ 2 |
|
|
|||||
t |
n / /( (1 )) 3 /12 0,25; t |
|
|
|
||||||||
Задание. Написать программу, реализующую данный алгоритм. Сделать подробные комментарии и инструкцию пользователя. Необходимые величины взять произвольными и найти оптимальные условия функционирования системы.
29
ЛАБОРАТОРНЫЕ РАБОТЫ
Численные методы одномерной минимизации
При выполнении лабораторных работ 1-4 студенты должны изучить и реализовать различные методы минимизации, оформить итоговый отчёт. Задания сформулированы в соответствующих разделах.
Лабораторная работа 1. Классический метод минимизации. Метод деления отрезка пополам.
Лабораторная работа 2. Метод "золотого сечения".
Лабораторная работа 3. Метод парабол.
Лабораторная работа 4. Метод Ньютона одномерной минимизации.
Выпуклые множества и выпуклые функции
Лабораторная работа 5. Выполнить задания сформулированные в соответствующем разделе.
Численные методы многомерной минимизации
При выполнении лабораторных работ 6-10 студенты должны изучить и реализовать различные методы минимизации, оформить итоговый отчёт. Задания сформулированы в соответствующих разделах.
Лабораторная работа 6. Метод дробления шага.
Лабораторная работа 7. Метод наискорейшего спуска. Лабораторная работа 8. Метод Ньютона многомерной минимизации. Лабораторная работа 9. Метод штрафных функций. Лабораторная работа 10. Метод барьерных функций.
При выполнении лабораторных работ 11-14 студенты должны выполнить задания, сформулированы в соответствующих разделах, оформить итоговый отчёт.
Лабораторная работа 11. Задача продавца газет. Лабораторная работа 12. Задача управления запасами. Лабораторная работа 13. Задача теории расписаний.
Лабораторная работа 14. Элементы теории массового обслуживания.
30
