
kostrub_lab_method
.pdfсоответственно |
|
u1 0,7; u2 |
0,9 .Значения |
целевой |
функции |
||
J (u1 ) 0,17493; J (u2 |
) 0,13851 |
связаны соотношением |
J (u1 ) J (u2 |
) , |
|||
поэтому полагаем a3 |
a2 0,6; b3 |
u2 |
0,9 . |
|
|
|
|
Аналогичные вычисления продолжаем осуществлять до тех пор, пока длина рассматриваемого нами отрезка не станет меньше, чем .
2. Исследовать на минимум функцию J (u) u3 (u 2 1) при условии, что
u [0,1] . |
|
|
|
|
|
|
|
|
|
|
Пусть a1 |
0; b1 |
1 . Точки "золотого |
сечения" |
соответственно равны |
||||
u1 |
0,382 u2 0,618 . |
Целевая |
функция |
в них |
принимает |
значение |
|||
J (u1 ) 0,326; J (u2 ) 0,382 . |
Так |
как |
J (u1 ) J (u2 ) , |
то |
полагаем |
||||
a2 |
u1 ; b2 a1 ; u2' |
u2 . |
Осуществляя |
последовательно |
все необходимые |
||||
действия получим, что u* 0,618; J (u* ) 0,382 .
Задание. Найти решение задачи одномерной минимизации
J (u) inf u a, b .
Значения коэффициентов целевой функции
J (u) a0u5 a1u 4 a2u3 a3u 2 a4u a5
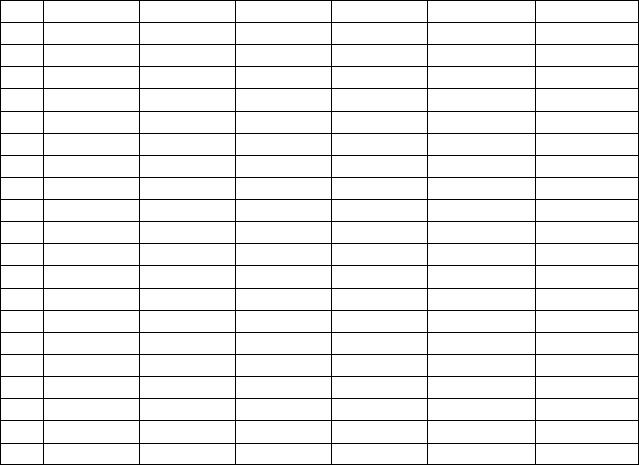
приведены в таблице. Помимо точек минимума посчитать число итераций и сделать вывод о целесообразности использования каждого из методов в той или иной ситуации. Приближенное решение задачи искать на промежутке унимодальности a,b с точностью до 10 2 методом: а) деления отрезка
пополам; б) "золотого сечения"; в) парабол; г) Ньютона. Решение поставленной задачи оформить в виде отчёта.
Замечание: для нахождения промежутка унимодальности найдите J (u) , затем корни уравнения J (u) 0 . Промежутки, в которых J (u) 0 и будут отрезками унимодальности J (u) .
Для метода Ньютона выбор начального приближения рекомендован в алгоритме.
N |
a0 |
a1 |
a2 |
|
a3 |
a4 |
a5 |
1 |
1 |
0 |
2 |
|
0 |
1 |
-1 |
2 |
1 |
0 |
-2 |
|
0 |
1 |
-2 |
3 |
1 |
0 |
-1 |
|
0 |
-2 |
-3 |
4 |
1 |
0 |
1 |
|
0 |
-2 |
1 |
|
|
|
|
11 |
|
|
|
5 |
1 |
0 |
-1 |
0 |
1/4 |
2 |
6 |
1 |
0 |
-1 |
0 |
-8 |
3 |
7 |
1 |
0 |
1 |
0 |
-8 |
4 |
8 |
1 |
0 |
1/3 |
0 |
-4 |
-4 |
9 |
1 |
0 |
-1/3 |
0 |
-4 |
5 |
10 |
1 |
0 |
2/3 |
0 |
-3 |
-5 |
11 |
1 |
0 |
-2/3 |
0 |
-3 |
6 |
12 |
1 |
0 |
-3 |
0 |
-2 |
1 |
13 |
1 |
0 |
-3 |
0 |
-2 |
4 |
14 |
1 |
0 |
2 |
0 |
-2 |
-3 |
15 |
1 |
0 |
2 |
0 |
-2 |
-1 |
16 |
1 |
0 |
1 |
0 |
-1 |
-2 |
17 |
1 |
0 |
-1 |
0 |
2 |
2 |
18 |
1 |
0 |
2 |
0 |
-2 |
3 |
19 |
1 |
0 |
1 |
0 |
-3 |
-3 |
20 |
1 |
0 |
-1 |
0 |
4 |
-4 |
21 |
1 |
0 |
-4 |
0 |
1 |
1 |
22 |
1 |
0 |
4 |
0 |
4 |
-3 |
23 |
1 |
0 |
3 |
0 |
3 |
1 |
24 |
1 |
0 |
-3 |
0 |
3 |
-1 |
25 |
1 |
0 |
1/2 |
0 |
-2 |
2 |
ВЫПУКЛЫЕ МНОЖЕСТВА И ВЫПУКЛЫЕ ФУНКЦИИ
Определение. |
Пусть U X . Будем |
говорить, что U выпуклое |
||
множество, если для любых двух элементов |
u1,u2 множества U |
элемент |
||
u1 (1 )u2 также |
принадлежит множеству U , где |
0,1 . |
Пустое |
|
множество выпукло по определению. |
|
|
|
|
Определение. |
Функция J : U X R |
называется |
выпуклой, если |
|
выполняется неравенство |
|
|
|
|
|
J u1 (1 )u2 J u1 (1 )J u2 |
|
|
|
для любых элементов u1,u2 множества U .
|
ПРИМЕРЫ |
1. При каких значениях |
параметра a функция одной переменной |
J (u) au 2 bu c является выпуклой? |
|
Воспользуемся определением. Для выпуклой функции должно |
|
выполняться неравенство J u1 |
(1 )u2 J u1 (1 )J u2 . Проверим, так |
ли это.
12

J u |
(1 )u |
2 |
a( u |
1 |
(1 )u |
2 |
)2 b( u |
|
(1 )u |
2 |
) c |
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
a( |
2u 2 2 1 u u |
2 |
(1 )2 u 2 ) b( u |
|
1 u |
2 |
) c |
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
(au 2 |
bu c) au 2 |
c (1 )(au 2 |
bu |
2 |
c) (1 )au 2 |
|
|
|
|||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
(1 )c 2 au 2 2 a(1 )u u |
2 |
a(1 )2 u 2 |
c |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
J (u ) |
(1 |
) f (u |
2 |
) |
(1 |
)au 2 |
|
2 (1 |
)au u |
2 |
(1 )(1 1 |
)au 2 |
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
||
J (u ) |
(1 |
)J (u |
2 |
) |
(1 |
)a(u |
2 |
2u u |
2 |
u |
2 ) |
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
J (u ) |
(1 |
)J (u |
2 |
) |
(1 |
)(u |
1 |
u |
2 |
)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получаем, что J u1 |
|
(1 )u2 J u1 |
(1 )J u2 при |
|
a 0 . |
|
|
|
|||||||||||||||||||||||||
2. Является ли выпуклой функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
J (u) u ln u (1 u) ln(1 u) , |
u (0,1) ? |
|
|
|
|||||||||||||||||||||
Поскольку для выпуклой функции выполнено неравенство 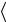 J (u) ,
J (u) ,  0 , где u U , то воспользуемся этим.
0 , где u U , то воспользуемся этим.
J (u) ln u 1 1 ln(1 u) ,
J (u) u1 1 1 u .
Вторая производная всегда больше нуля, так как 1 u u 0 при u U . u(1 u)
3. Является ли выпуклой функция
J (u1 , u2 ) a11u12 2a12u1u2 a22u22 ?
Посчитаем первую производную и вторую производные
|
|
J |
|
2a11u1 2a12u2, |
|
|
J |
|
|
2a12u1 2a22u2 . |
|||||||||||
|
|
u |
|
u |
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вторая производная для данной функции |
|
|
|
|
|
||||||||||||||||
|
2 J 2a11 , 2 J 2a22 |
, |
2 J |
|
|
|
2 J |
|
2a12 . |
||||||||||||
|
u |
|
u |
|
|
u |
u |
|
|||||||||||||
|
u 2 |
u 2 |
|
|
|
|
2 |
|
|
1 |
|
||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
||||
Матрица вторых производных имеет вид |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2a |
|
|
2a |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
11 |
|
|
2a |
12 . |
|
|
|
|
|
||||||
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|||||
Условие |
J (u) , 0 |
|
|
12 |
|
|
|
|
|
22 |
|
|
|
|
|
||||||
выполнено тогда и только тогда, когда |
|||||||||||||||||||||
J (u) , min |
|
|
|
|
|
|
|
|
|
|
|
min 0 . Для этого посчитаем |
|||||||||
, 0 , а оно выполнено при |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определитель матрицы |
|
2a |
|
|
|
2a |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
11 |
|
2a |
|
|
12 |
|
|
. |
|
|
|
|||||
|
|
|
|
|
2a |
|
22 |
|
|
|
|
|
|||||||||
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||
инайдем min . Получаем уравнение 2 2 (a11 a22 ) 4(a122 a11a22 ) . Корни его
(a11 a22 ) 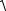 (a11 a22 )2 4a122 . Т.е. (a11 a22 )
(a11 a22 )2 4a122 . Т.е. (a11 a22 ) 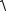 (a11 a22 )2 4a122 . Возводя в
(a11 a22 )2 4a122 . Возводя в
квадрат и преобразуя получаемое выражение, получим систему
13
a11a22 a122 , a11 a22 0
откуда следует, что min 0 .
4. Исследовать области выпуклости и вогнутости функции
J (u1 , u2 ) u13 / 6 u23 / 6 u12 / 2 u22 u1u2 2u1 .
Составим матрицу Гессе и вычислим главные миноры
u 1 |
|
|
1 |
; |
|
|
|
|
u 1; |
|||||
|
1 |
u |
|
2 |
|
|
|
(u |
|
1 |
1 |
|
1) 1. |
|
|
1 |
2 |
|
2 |
2 |
2)(u |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
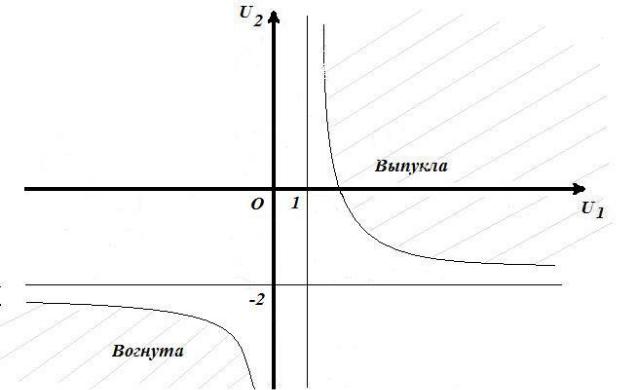
Функция J выпукла в любой области, где матрица Гессе неотрицательно определена. Область положительной определённости определяется условиями 1 u1 1 0 , 2 (u2 2)(u1 1) 1 0 ,
обеспечивающими строгую выпуклость. Выпуклость будет на замыкании этого множества. Функция J вогнута в любой выпуклой области, где матрица Гессе неположительно определена. Область её отрицательной определенности определяется условиями 1 u1 1 0 , 2 (u2 2)(u1 1) 1 0 ,
обеспечивающими строгую вогнутость. Вогнутость будет на замыкании этого множества.
Рис. 5
14
Итак, функция |
выпукла |
на |
любом подмножестве множества |
{(u1 , u2 ) : u2 1 1/(u1 1),u1 |
1} и вогнута на любом выпуклом подмножестве |
||
множества {(u1 , u2 ) : u2 1 1/(u1 1),u1 |
1} |
(см. рис. 5). |
|
Задания. 1. Выяснить, влияют ли линейные члены квадратичной функции на её выпуклость?
2. Построить вид областей выпуклости и вогнутости следующих функций:
2.1.J (u1 , u2 ) (u1 1)3 (u2 1)3 ;
2.2.J (u1 , u2 ) (u1 1) (u2 1)3 6u1u2 .
3. Построить вид областей выпуклости и вогнутости функций в зависимости от параметра p :
3.1.J (u1 , u2 ) pu12 u1u2 pu22 ;
3.2.J (u1 , u2 ) pu12 4u1u2 u22 ;
3.3.J (u1 , u2 ) u13 pu23 .
ЧИСЛЕННЫЕ МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ
Пусть функция n переменных J (u1 ,..., un ) задана на некотором множестве пространства Rn . Известно, что если J (u) дифференцируема в точке P(u1 ,..., un ) , то в этой точке существуют частные производные
J (u1 ,..., un ) , i 1,..., n
ui
и наоборот, если фукнция J (u1 ,..., un ) имеет частные производные по всем аргументам в некоторой окрестности точки P0 (u10 , u20 ,..., un0 ) , причем все эти частные производные непрерывны в самой точке P0 , то указанная функция дифференцируема в точке P0 .
Определение. Говорят, что функция J (u) имеет в точке P0 локальный
максимум (локальный минимум), если найдется такая -окрестность точки P0 , в пределах которой значение J (P0 ) является наибольшим (наименьшим)
среди всех значений J (u) этой функции.
Если функция J (u1 ,...,un ) обладает в точке P0 (u10 , u20 ,..., un0 ) частными производными первого порядка по всем переменным (u1 ,...,un ) и имеет в этой
точке локальный экстремум, то все частные производные первого порядка обращаются в точке P0 в нуль, т.е.
15

J |
(P ) 0, |
J |
(P ) 0,..., |
J |
(P ) 0. |
|
|
|
|||
0 |
u2 |
0 |
un |
0 |
|
u1 |
|
|
|||
Определение. Точки, в которых обращаются в нуль все частные производные первого порядка функции J (u) , называются стационарными
точками этой функции.
МЕТОД ГРАДИЕНТНОГО СПУСКА
Метод градиентного спуска использует условие дифференцируемости функции J (u) в Rn . В качестве критерия остановки этого метода, как
правило, выбирается условие || grad J (u k ) || . В качкестве направления
движения для нахождения минимума в метода градиентного спуска на каждом шаге выбирается вектор-антиградиент vk grad J (u k ) , так как в
малой окрестности точки uk антиградиент обеспечивает наискорейшее убывание функции. Рассмотрим два варианта метода, отличающиеся способом нахождения величины .
Замечание. Если |
J (u) J (u1 , u2 ,...,un ) , то |
|
J |
|
J |
|
J |
|
, а |
|||
|
, |
,..., |
|
|||||||||
u |
u |
|
u |
|
||||||||
grad J (u) |
2 |
|
|
|||||||||
|
|
|
1 |
|
|
|
|
n |
|
|||
|
|
J |
|
2 |
J |
|
|
2 |
|
J |
|
2 |
* |
|
|||
|| grad J (u) || |
|
|
|
|
|
|
|
|
. Точка u |
- точка минимума функции |
|||||||
u |
u |
|
|
|
u |
|
|
||||||||||
|
|
|
|
|
|
|
... |
|
|
|
|||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
J (u) , а J (u* ) |
- значение функции в точке минимума. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
АЛГОРИТМ |
|
|
||||
|
|
|
|
|
|
|
|
(метод дробления шага) |
|||||||||
Шаг 1. Задать 0 |
- требуемую точность, начальный шаг 0 . Выбрать |
||||||||||||||||
u0 Rn |
и вычислить J (u0 ) . |
|
|
|
|
|
|
||||||||||
Шаг 2. Найти grad J (u0 ) |
и проверить критерий остановки метода |
||||||||||||||||
|| grad J (u0 ) || . Если он выполнен, то вычисления завершаются. |
|||||||||||||||||
Полагаем u* |
u0 , |
J * |
J (u0 ) . |
|
|
|
|
|
|
||||||||
Шаг 3. Положить u1 |
u0 |
grad J (u0 ) . Вычислить J (u1 ) . |
|||||||||||||||
Если J (u1 ) J (u0 ) , то положить u0 u1 и J (u0 ) J (u1 ) . Перейти к шагу 2. |
|||||||||||||||||
Шаг 4. Положить / 2 и перейти к шагу 3. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
АЛГОРИТМ |
|
|
||||
|
|
|
|
(метод наискорейшего спуска) |
|||||||||||||
Шаг 1. Задать 0 |
- требуемую точность. Выбрать u0 Rn . |
||||||||||||||||
Шаг 2. Найти grad J (u0 ) |
и проверить критерий остановки метода |
||||||||||||||||
|| grad J (u0 ) || . Если он выполнен, то вычисления завершаются. |
|||||||||||||||||
Полагаем u* |
u0 , |
J * |
J (u0 ) . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
Шаг 3. Решить задачу одномерной оптимизации
( ) J (u0 grad J (u0 )) min , при 0 , т.е. найти * . Положить u0 u0 * grad J (u0 ) . Перейти к шагу 2.
Замечание. Кроме рассмотренных методов выбора шага на практике часто применяют методы с изначально заданным шагом, например,
k 1/(k 1) , где k - номер итерации.
МЕТОД НЬЮТОНА МНОГОМЕРНОЙ МИНИМИЗАЦИИ
Итерационный метод вида u k 1 u k * grad J (u k )H 1 носит название
метода Ньютона. В этой формуле H 1 - это обратная матрица к матрице вторых частных производных
|
|
|
2 |
J |
|
|
|
2 |
J |
|
|
|
|
|
2 |
J |
|
|
|||||
|
|
|
|
|
|
|
|
|
... ... |
|
|
|
|
|
|||||||||
|
u 2 |
|
|
u |
|
|
u |
|
u |
|
|
u |
|
||||||||||
|
|
|
|
2 |
1 |
n |
1 |
|
|||||||||||||||
H |
|
|
|
|
1 |
|
|
|
... |
|
|
|
|
|
|
|
|||||||
|
... |
|
|
|
|
|
|
|
|
|
... |
|
|
|
. |
||||||||
|
|
2 J |
|
|
2 J |
|
|
... ... |
2 J |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
u |
|
u |
|
|
u |
|
|
u |
|
|
u 2 |
|
||||||||||
|
|
|
n |
|
2 |
n |
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||
Для квадратичной функции с положительно определённой матрицей Гессе применение метода Ньютона с шагом 1 обеспечивает получение точки глобального минимума ровно за одну итерацию, независимо от выбора начальной точки. Для выпуклой квадратичной функции применение этого метода обеспечивает, как правило, быструю сходимость. Однако, если точка u0 Rn выбрана недостаточно близко к оптимальному решению, то последовательность u k Rn может расходиться (как и в одномерном случае). Существенным недостатком метода Ньютона является необходимость вычисления и обращения матрицы Гессе на каждой итерации.
АЛГОРИТМ
Шаг 1. Задать начальную точку u0 Rn , 0 - требуемую точность, вычислить J (u0 ) .
Шаг 2. Найти grad J (u0 ) и проверить критерий остановки метода
|| grad J (u0 ) || . Если он выполнен, то вычисления завершаются. Полагаем u* u0 , J * J (u0 ) .
Шаг 3. Положить u0 u0 grad J (u0 ) H 1 . Вычислить J (u0 ) . Перейти к шагу 2.
17

МЕТОД ШТРАФНЫХ ФУНКЦИЙ
Основная идея метода штрафных функций состоит в преобразовании задачи минимизации функции с соответствующими ограничениями в задачу поиска минимума функции без ограничений.
Преимущество, которое получаем в результате такого перехода к новой функции, достигается за счет применения более простых алгоритмов.
Постановка задачи. Требуется найти минимум функции J (u1 ,...,un ) при ограничениях gi (u1 ,...,un ) 0, i 1,2,..., m или
J (u1 ,..., un ) inf,
gi (u) 0, i 1,2,..., m .
Введём функцию
F(u1 ,..., un ) J (u1 ,...,un ) P(u1 ,..., un ) .
Здесь P(u1 ,..., un ) выступает в роли штрафа. Штраф можно выбрать в виде
m
P(u1 ,..., un ) r | 1/ gi (u1 ,..., un ) |
i 1
или в виде
m
P(u1 ,..., un ) r gi 2 (u1 ,..., un ) ,
i 1
где 

 - некоторый положительный параметр.
- некоторый положительный параметр.
ПРИМЕРЫ
1. Один из вариантов выбора штрафной функции таков. Пусть дана функция J (u1 , u2 ) u1 (u2 1)2 при ограничениях u1 2, u2 0 . Выберем штраф
P(u1 , u2 ) r | 1/(u1 2) 1/ u2 | .
В результате минимизируем функцию
F(u1 , u2 , r) u1 (u2 1)2 r | 1/(u1 2) 1/ u2 | .
18

2. Ещё один из вариантов выбора штрафной функции. Требуется
минимизировать |
функцию |
J (u1 , u2 ) (u1 3)2 (u2 |
2)2 , при ограничении |
|||||||
u1 u2 4 0 . |
|
|
|
|
|
|
|
|
|
|
Прибавим к |
целевой |
|
функции |
значение |
rg 2 (u1 ,u2 ) , тогда получим |
|||||
функцию без ограничений |
|
|
|
|
|
|
|
|
|
|
|
F(u , u |
, r) (u 3)2 |
(u |
2 |
2)2 r(u u |
2 |
4)2 |
|||
|
1 |
2 |
|
1 |
|
|
1 |
|
||
Таким образом, методы штрафных функций определяются как выбором вида штрафа, так и выбором параметра r.
3. Рассмотрим теперь один из параметрических методов (метод внутренней точки).
Пусть требуется минимизировать функцию J (u1 , u2 ) u12 6u1 u22 9u2 при ограничениях ui 0, i 1,2.
Исходная точка поиска A0 (1;0,5) .
1. Строим функцию без ограничений, используя штраф
|
|
P(u , r) J (u ) r 1 |
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
, r) u 2 |
|
u 2 |
i 1 |
gi ( |
u |
) |
|
|
|
|
||||||
P(u , u |
2 |
6u |
9u |
2 |
r(1/ u |
1/ u |
2 |
) |
||||||||||
1 |
1 |
1 |
2 |
|
|
|
|
1 |
|
|
||||||||
2.Пусть r0 1. Найдем минимум функции P(u1 , u2 , r0 ) любым методом безусловной оптимизации, например, градиентным
|
|
P |
|
|
|
|
|
2 |
) A0 2 1 6 1 7 ; |
||||
|
|
|
|
|
|
|
|||||||
|
u |
(2u1 |
6 1/ u1 |
||||||||||
|
|
|
|||||||||||
|
|
1 |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
2 |
2 0,5 9 1/ 0,25 6 ; |
||||
|
|
|
|
|
|
|
|||||||
|
|
(2u2 9 |
1/ u2 ) A0 |
||||||||||
|
u2 |
|
|||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0,05 ; |
|
|
|
|
|
|
2 P |
0 |
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
u |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
2 P |
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
u22 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
19
|
1 |
|
|
0 |
|
|
|
P |
|
|
1 0,05 7 0,55 ; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
u1 |
|
u1 |
|
|
u |
|
||||||||||||||
|
|
|
0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
A |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
P |
|
|
0,5 0,05 6 0,2 ; |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
u2 |
u |
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
u2 |
A |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
0,018 ; |
|||||
|
|
|
|
3,7; |
|
|
|
|
15,6; 1 |
|||||||||||||
|
u |
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
u |
|
|
|
||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
2 A |
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
P |
|
|
0,483 ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
u1 |
u1 |
|
|
|
|
|
u |
|
|||||||||
|
|
|
|
|
|
1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
A |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
P |
|
|
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
u2 |
u2 |
|
|
|
|
0,48 |
|||||||||||
|
|
|
|
|
1 |
u |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 A |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
A1 (0,483;0,48) . |
|
|||||||||||||
Итак далее. Получим AОпт (r0 ) (0,38;0,325); PОпт (r0 ) 11,16 .
3.Уменьшаем r. Полагаем r1 r0 / C, C 1. Пусть C 10 . Минимизируем P(u1 , u2 , r1 ) тем же градиентным методом, теперь за исходную точку
принимаем A0 (0,38;0,325) .
|
|
|
P |
|
|
|
|
|
|
|
6,07 ; |
||
|
|
|
|
|
|
|
2 |
|
|||||
|
u |
(2u1 |
6 0,1/ u1 |
) A0 |
|||||||||
|
|
|
|||||||||||
|
|
|
|
1 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
8,7 ; |
||
|
|
|
|
|
(2u |
2 9 0,1/ u |
2 |
||||||
|
|
|
|
|
|
2 ) A0 |
|||||||
|
|
|
u2 |
|
|
||||||||
|
|
|
|
A |
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,02 ; |
|
|
||
|
|
|
|
|
|
|
|
P |
|
|
0,38 0,02 6,07 0,26 ; |
||
1 |
|
0 |
|
|
|
|
|
|
|||||
u1 |
u1 |
|
|
u |
|||||||||
0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
P |
|
|
0,38 0,02 6,07 0,26 ; |
||
1 |
|
0 |
|
|
|
|
|
|
|||||
u2 |
u2 |
|
|
|
|
||||||||
0 |
u2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
||
0
И так далее. Получим AОпт (r1 ) (0,127;0,106); PОпт (r1 ) 3,47 . 4. Вновь уменьшаем r. Полагаем r2 r1 / C и т. д.
20
