
kostrub_lab_method
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО МЕТОДАМ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЮ ОПЕРАЦИЙ
Составитель И.Д. Коструб
Издательско-полиграфический центр Воронежского государственного университета
2013
Утверждено научно-методическим советом факультета прикладной математики, информатики и механики 19 февраля 2013 г., протокол № 6
Рецензент доцент кафедры ММИО Ю.В. Бондаренко
Практикум подготовлен на кафедре нелинейных колебаний факультета ПММ Воронежского государственного университета.
Рекомендуется для студентов 3-го курса дневного отделения.
Для специальности 010501 – Прикладная математика и информатика

Лабораторный практикум написан по курсу «Методы оптимизации и исследование операций» и посвящён численным методам минимизации функций одной и нескольких переменных, а также решению задач курса «Исследование операций» с помощью ЭВМ. Предназначен практикум для лабораторной и самостоятельной работы студентов. В каждом параграфе приводятся теоретические сведения, необходимые для решения сформулированных задач. Приводятся образцы решения задач, а также задания для самостоятельной работы.
ЧИСЛЕННЫЕ МЕТОДЫ МИНИМИЗАЦИИ
Определение. Пусть функция J (u) определена всюду в некоторой
окрестности точки P . Тогда эта функция имеет в точке P локальный максимум (или соответственно локальный минимум), если существует такая окрестность точки P , что для всех точек этой окрестности значение J (P)
является наибольшим (или соответственно наименьшим) среди всех значений J (u) этой функции.
Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.
Если функция J (u) |
дифференцируема в данной точке P и имеет в этой |
|
точке локальный |
экстремум, то J (u) 0 . Точки, в которых производная |
|
J (u) 0 функции |
J (u) |
|
обращается в нуль, называются стационарными |
||
|
|
|
точками функции. Каждая стационарная точка – это точка возможного экстремума функции. Однако сделать заключение о том, что в данной стационарной точке на самом деле имеется экстремум, можно лишь на основании дополнительного исследования, для проведения которого существуют достаточные условия экстремума.
ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
КЛАССИЧЕСКИЙ МЕТОД МИНИМИЗАЦИИ
Численные методы минимизации составной своей частью содержат поиск точек локального минимума функции вдоль заданного направления, т.е отыскание точек минимума функции одной переменной (как правило, на заданном отрезке).
Постановка задачи. Найти решение следующей задачи
J (u) inf
u U a, b ,
где J (u) действует следующим образом J : X R , X - это область определения, причём U X . Точки u U называются допустимыми, а J (u) - целевой функцией.
3
Теорема (Вейерштрасса). Если U замкнуто и ограничено, а J (u) непрерывна на нем, то функция J (u) ограничена снизу на этом множестве.
Пусть функция J (u) кусочно-непрерывна и кусочно-дифференцируема. Подозрительными на экстремум считаются следующие точки:
1.Стационарные J (u) 0 .
2.Концы отрезка (краевой максимум и краевой минимум объединяют общим названием - краевой экстремум).
3.Точки разрыва.
4.Точки, в которых производная не существует.
5.Точки разрыва производной.
Затем следует провести дополнительные исследования в стационарных точках.
Пусть J (P0 ) J (P0 ) ... J (k ) (P0 ) 0 , а |
J (k 1) (P0 ) 0 . |
|
||||
Если (k 1) четная и |
J (k 1) (P0 ) 0 , |
то |
P0 - точка минимума; |
если |
||
(k 1) четная и J (k 1) (P0 ) 0 , то P0 |
- точка максимума. |
|
||||
Если (k 1) нечетная, то P0 |
- точка перегиба. |
|
||||
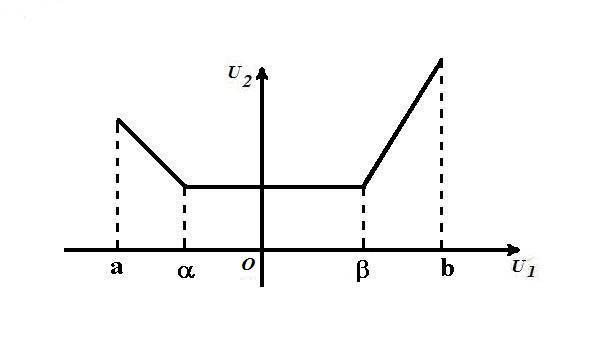
Определение. Функция |
J : U R |
называется унимодальной на |
||||
U a, b , если существуют числа |
a b , |
такие, что на отрезке |
[a, ] |
|||
функция убывает, на отрезке [ ,b] |
возрастает, а на отрезке [ , ] остается |
|||||
постоянной (см. рис. 1). |
|
|
|
|
|
|
Рис. 1
4
МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
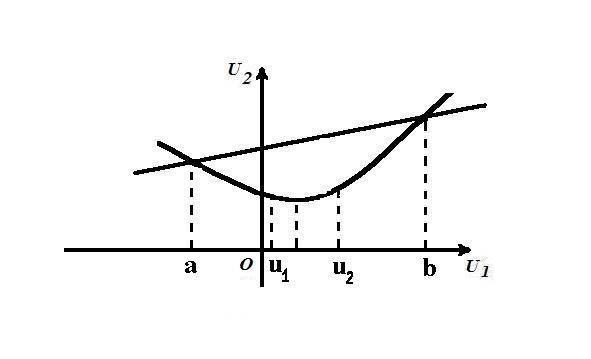
Рассмотрим метод деления отрезка пополам, предполагая, что целевая функция является унимодальной на рассматриваемом отрезке. Заметим, что выпуклая на отрезке a,b функция является унимодальной на нём, поэтому для
дважды непрерывно дифференцируемой на (a, b) функции J (u) условие
неотрицательности |
второй |
производной J"(u) 0 , |
u (a, b) |
является |
достаточным для унимодальности функции на отрезке a, b . |
|
|||
Нахождение |
точки |
u* [a,b] доставляющей |
локальный |
минимум, |
осуществляется путем последовательного уменьшения отрезка, содержащего точку минимума.
и |
Для сужения отрезка унимодальности будут использоваться две точки u1 |
|||||||
u2 , расположенные |
симметрично относительно |
середины |
отрезка |
|||||
u1 |
(b a ) / 2 , u2 (b a ) / 2 , |
0 (b a) / 2 ; |
причем u1 , u2 |
[a, b] |
и u1 u2 . В |
|||
каждой из трех возможных ситуаций длина отрезка |
[u1 , u2 ] |
не |
должна |
|||||
превышать (b a ) / 2 . |
Если |
величина |
мала, |
то |
длина |
отрезка |
||
унимодальности уменьшается почти вдвое, чем и мотивировано название метода.
Рис. 2
АЛГОРИТМ
Шаг 1. Положить n 0 , задать a, b, , .
Шаг 2. Положить n n 1, u1 (b a ) / 2 , u2 (b a ) / 2 . Шаг 3. Вычислить J1 J (u1 ) , J 2 J (u2 ) .
5
Шаг 4. Сравнить J1 и J 2 .
Если J1 J 2 , то b u2 и перейти к шагу 5. Если J1 J 2 , то a u1 и перейти к шагу 5.
Если J1 J 2 , то b u2 , a u1 и перейти к шагу 5.
Шаг 5. Если (b a) , то перейти к шагу 2, иначе положить u* (b a) / 2 ,
J* J (u* ) .
Все описанные выше шаги выполняются до тех пор, пока длина рассматриваемого отрезка больше или равна заданного малого числа . Чтобы
вычисления были максимально точными, число необходимо выбирать достаточно маленьким. Если оно большое, то полагают / 2 и вычисления повторяют.
МЕТОД «ЗОЛОТОГО СЕЧЕНИЯ»
Рассмотрим метод "золотого сечения", предполагая, что целевая
функция является унимодальной на рассматриваемом отрезке. Напомним, что |
||
нахождение точки |
u a, b |
доставляющей локальный минимум, |
осуществляется путём последовательного уменьшения отрезка, содержащего точку минимума. В методе "золотого сечения" для сужения отрезка унимодальности будут использоваться две точки u1 и u2 , выполняющие
"золотое сечение" данного отрезка.
Определение. Будем говорить, что точка u осуществляет "золотое сечение" отрезка [0, A] , если выполняется соотношение
A |
|
u |
|
|
, |
||
|
u |
|
A |
u |
|
||
|
|
|
|
|
|||
т.е. если отношение длины отрезка к большей его части равно отношению большей части к меньшей (см. рис. 3).
6

|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть точка u1 осуществляет "золотое сечение" отрезка a, b . |
|||||||||||||||||||||
Поскольку u a, b , то u a (b a) , 0 1. Если длина отрезка a, u |
больше |
||||||||||||||||||||
длины отрезка u,b , то |
удовлетворяет соотношению |
|
1 |
|
|
|
|
. Откуда, |
|||||||||||||
|
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
учитывая положительность , получаем, что |
|
|
5 1 |
|
. Если же большей |
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
является длина отрезка |
u, b , то удовлетворяет соотношению |
1 |
|
|
1 |
. |
|||||||||||||||
1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Откуда в силу того, что |
3 |
|
5 |
|
|
|
|
|
мы показали, что |
||||||||||||
1 , получаем |
|
. Значит, |
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки u1 |
и u2 , вычисляемые соответственно по формулам |
u1 |
|
3 |
5 |
|
|
|
|
||||||||||||
|
|
b a a |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5 1 |
|
|
сечение" |
отрезка |
[a,b] . Эти |
|||||||||||||||
и u2 |
|
b a a осуществляют "золотое |
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точки расположены симметрично относительно середины отрезка. Кроме того, |
||||||||||
точка u1 |
является "золотым сечением" отрезка a,u2 |
( u1 a u2 |
u1 ); а точка u2 |
|||||||
является |
"золотым сечением" отрезка u1 , b |
( b u2 |
u2 u1 );. |
Отметим, что |
||||||
|
5 1 |
2 |
|
3 |
5 |
|
|
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
2 |
|
|
|
|
|
АЛГОРИТМ
|
|
|
|
|
5 1 |
3 |
5 |
|||||
Шаг 1. Положить n 0 , задать a, b, . Положить |
|
|
|
и 1 |
|
|
. |
|||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
Шаг 2. Положить u1 a 1 (b a) , u2 a (b a) . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
Шаг 3. Положить n n 1 и вычислить J1 J (u1 ) , J 2 |
J (u2 ) . |
|
|
|
|
|||||||
Шаг 4. Сравнить J1 и J 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
Если J1 J 2 , то положить b u2 , u2 |
u1 , |
J 2 |
J1 , u1 |
a 1 (b a) , |
|
|
||||||
J1 J (u1 ) . Перейти к шагу 5. |
|
|
|
|
|
|
|
|
|
|
|
|
Если J1 J 2 , то положить a u1 , u1 |
u2 , |
J1 |
J 2 |
, u2 |
a (b a) , |
|
|
|||||
J 2 J (u2 ) . Перейти к шагу 5. |
|
|
|
|
|
|
|
|
|
|
|
|
Если J1 J 2 , то b u2 , a u1 , u1 a 1 (b a) , |
u2 |
a (b a) , |
J1 J (u1 ) , |
|||||||||
J 2 J (u2 ) . Перейти к шагу 5. |
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 5. Если (b a) , то перейти к шагу 3, иначе положить u* (b a) / 2 ,
J* J (u* ) .
Все описанные выше шаги выполняются до тех пор, пока длина рассматриваемого отрезка больше или равна заданного малого числа .
7
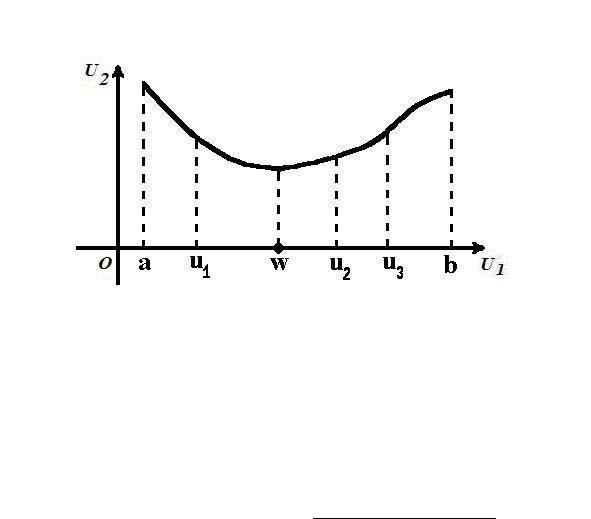
МЕТОД ПАРАБОЛ
Рассмотрим метод парабол. Предполагаем, что целевая функция является унимодальной на рассматриваемом отрезке. Суть метода состоит в последовательном сужении отрезка, содержащего точку минимума, используя аппроксимацию функции на этом отрезке полиномом второго порядка.
Определение. Тройка точек u1 , u2 , u3 является выпуклой для функции J (u) , если справедливы следующие неравенства J (u1 ) J (u2 ) 0 ,
J (u3 ) J (u2 ) 0 , 0 .
|
Рис. 4 |
Пусть наша тройка выпукла. Тогда можно провести параболу |
|
f (u) 0u 2 |
1u 2 через точки с координатами (u1 , J (u1 )), (u2 , J (u2 )), (u3 , J (u3 )) . |
Функция |
f (u) будет совпадать с многочленом Лагранжа, построенным по |
указанным точкам. Причём точка w - точка минимума построенной параболы
вычисляется по следующей формуле w u2 (u3 u2 )2 (u2 u1 )2 . 2((u3 u2 ) (u2 u1 ) )
Возможны следующие варианты
1.Точка минимума параболы расположена слева от точки u2 , т.е. w u2 .
1.1.Если J (w) J (u2 ) , то новой выпуклой тройкой считаем (u1 , w, u2 ) , (т.е. промежуток унимодальности функции [u1 , u2 ] ).
8
1.2. Если J (w) J (u2 ) , то новой выпуклой тройкой считаем (w, u2 , u3 ) , (т.е. промежуток унимодальности функции [w, u3 ] ).
1.3. Если J (w) J (u2 ) , тогда:
1.3.1. Если J (u1 ) J (u2 ) , то новой выпуклой тройкой считаем (u1 , w,u2 ) . 1.3.2. Если J (u2 ) J (u3 ) , то новой выпуклой тройкой считаем (w, u2 , u3 ) .
2. Точка минимума параболы расположена справа от точки u2 , т.е. w u2 . 2.1. Если J (w) J (u2 ) , то новой выпуклой тройкой считаем (u2 , w, u3 ) , (т.е.
промежуток унимодальности функции [u2 , u3 ] ).
2.2. Если J (w) J (u2 ) , то новой выпуклой тройкой считаем (u1 , u2 , w) , (т.е. промежуток унимодальности функции [u1 , w] ).
2.3. Если J (w) J (u2 ) , тогда:
|
2.3.1. Если J (u3 ) J (u2 ) , то новой выпуклой тройкой считаем (u2 , w, u3 ) . |
||||
|
2.3.2. Если J (u1 ) J (u2 ) , то новой выпуклой тройкой считаем (u1 ,u2 , w) . |
||||
3. Точка минимума параболы совпадает с |
u2 , т.е. |
w u2 . В этом случае в |
|||
качестве новой тройки |
берём |
~ |
~ |
- любая точка отрезка |
|
(u1 ,u2 ,u3 ) , |
где u2 |
||||
(u1 |
~ |
|
~ |
|
|
, u3 ) , в которой J (u2 ) J (u2 ) и |
J (u2 ) J (u1 ) . Например, можно положить |
||||
~ |
~ |
в зависимости от того, что меньше J (u2 ) J (u2 ) |
|||
u2 |
u2 или u2 u2 |
||||
или J (u2 ) J (u2 ) . Если в обоих случаях значение функции в точке u2
меньше, то уменьшаем , пока либо не получим новую выпуклую тройку, либо не будет меньше заданной величины. В этом случае полагаем
u* u2 .
МЕТОД НЬЮТОНА ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Метод Ньютона является последовательным методом второго порядка. Предполагается, что функция J (u) дважды дифференцируема, причём
J (u) 0 (условие гарантирующее выпуклость функции J (u) ). В этом случае корень уравнения J (u) 0 можно приближённо искать методом касательных.
В отличие от предыдущих методов, метод Ньютона не относится к методу сокращения промежутков. Для начала работы метода вместо задания начального промежутка неопределённости требуется задание начальной точки u0 , в которой вычисляется J (u0 ) 0 и J (u0 ) 0 . В процессе работы
метода генерируется последовательность uk , k 1,2,... . В очередной точке uk строится линейная аппроксимация функции J (u) (касательная к графику J (u) ). Точка, в которой линейная аппроксимирующая функция обращается в
нуль, используется в качестве |
следующего приближения uk 1 . Уравнение |
касательной к графику J (u) в |
точке uk имеет вид v J (uk ) J (uk )(u uk ) , |
поэтому точка uk 1 , найденная из условия |
v 0 , определяется формулой |
9 |
|

uk 1 uk |
J (uk ) |
. Процедура нахождения точек uk продолжается до тех пор, |
|
J (uk ) |
|||
|
|
пока не будет достигнута требуемая точность, т.е. | J (uk ) | .
АЛГОРИТМ
Шаг 1. Задать начальную точку u0 , 0 - требуемую точность. Положить
k 0 .
Шаг 2. Вычислить J (uk ) .
Шаг 3. Если | J (uk ) | , то положить u* uk и J (u* ) J (uk ) и поиск завершить. Иначе перейти к шагу 4.
Шаг 4. Вычислить uk 1 uk J (uk ) .
J (uk )
Шаг 5. Положить k k 1. Перейти к шагу 2.
Исследования метода Ньютона показывают, что при достаточно близком к точке минимума u* выборе начального приближения u0 ,
гарантируется скорость сходимости последовательности uk , k 0,1,2,... к u* вида | uk u* | Cq2k , где q (0,1) , C 0 ; q и C зависят от выбора функции J (u) и выбора u0 . Если начальное приближение u0 выбрано не достаточно близко к точке u* , то последовательность uk , k 0,1,2,... метода Ньютона может
расходиться. В подобных случаях необходимо найти лучшее начальное приближение u0 , например, с помощью нескольких итераций метода "золотого
сечения".
|
|
|
ПРИМЕРЫ |
|
|
|
|
|
|
|
|
|
|
1. Исследовать на минимум функцию J (u) u3 (u 2 |
1) |
при условии, что |
|||||||||||
u [0,1] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сделаем несколько итераций методом деления отрезка пополам. |
|
||||||||||||
Пусть 0,2; 0,2 . Тогда значения переменных u1 , u2 |
на первом шаге |
||||||||||||
вычислений соответственно |
равны |
u1 0,4; u2 0,6 . |
Целевая |
функция |
в |
||||||||
посчитанных точках имеет значения |
J (u1 ) 0,05376; J (u2 ) 0,13824 . |
Так как |
|||||||||||
J (u1 ) J (u2 ) , то полагаем a1 |
u1 |
0,4; b1 b 1. |
|
|
|
u1 0,6; u2 |
0,8 |
|
|||||
На втором |
шаге |
вычисляем |
значения |
точек |
|
и |
|||||||
соответствующие |
значения |
целевой |
функции |
в |
посчитанных |
точках |
|||||||
J (u1 ) 0,13824; J (u2 |
) 0,18432 . |
Так |
как J (u1 ) J (u2 |
) , |
то |
полагаем |
|||||||
a2 u1 0,6; b2 b 1 .
Третий шаг вычислительной процедуры позволяет посчитать
10
