
Практикум по математическому анализу
.pdf
у=х2-2 1,5х+1,52-1,52+5, или у=(х-1,5)2+2,75; у-2,75=(х-1,5)2.
Следовательно, вершина параболы лежит в точке (1,5; 2,75)
6 у
5 
4
3
2 


 М
М
1 
х
3 |
2 |
1 |
0 |
1 |
2 |
3 |
2. Составить уравнения касательной и нормали к гиперболе
x |
2 |
|
y |
2 |
|
|
|
|
|||
9 |
8 |
||||
|
|||||
1
,
проведенной в точке М(-9;-8).
Решение
Уравнение касательной к кривой y=f(x) в точке M(x0;y0) имеет вид
y-y0=f (x0) (x-x0).
Уравнение касательной к кривой y=f(x) в точке M(x0;y0) имеет вид
y-y0=
|
1 |
|
|
f ' (x |
|
) |
|
|
0 |
||
|
|
|
(x-x0).
Найдем f (x0), используя производную неявной функции. Дифференцируем равенство для функции по х.
2x |
|
2y y' |
0, |
y y' |
|
x |
, y' f '(x) |
8x |
. |
Подставляя координаты точки |
||||
9 |
8 |
8 |
9 |
9y |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
М, получим f '(x |
0 ) f '( 9) |
8 ( 9) |
1. |
Следовательно |
||||||||||
9 |
( 8) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
у+8=1 (х+9), или у=х+1–уравнение касательной; у+8=-1 (х+9), или у=-х-17–уравнение нормали. Сделаем чертеж, учитывая, что полуоси гиперболы а=3,
b |
8 2,8. |
|
у |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
М |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Ответ: у=х+1–уравнение касательной;

у=-х-17–уравнение нормали.
3. Найти производные данных функций в произвольной точке:
а)
|
1 cos |
2 |
x |
||
y |
|
||||
1 |
sin 5x |
||||
|
|||||
Воспользуемся правилами и формулами нахождения производной:
- производная частного 2-х функций |
( |
u |
) |
u v u v |
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
v2 |
|
|
|
|
|
|
|
|
|
- производная сложной функции ( f (u(x))) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
f (u(x)) u (x) |
|
|
||||||||||||||||||||
-формулами |
(sin x) |
|
cos x |
(cos x) |
|
sin x |
(x |
n |
) |
|
n x |
n 1 |
|
||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
x |
|
|
|
||||
|
1 cos |
) |
|
1 cos x 1 sin 5x 1 cos |
|
1 sin 5x |
|
||||||||||||||||
y ( |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
1 sin 5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 sin 5x |
|
|
|
|
|
|
|
|
|||||||||
|
2cosx sin x 1 sin 5x |
|
2 |
x 5cos5x |
|
|
|
|
|
|
|
|
|||||||||||
|
1 cos |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 sin 5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
y x arcsin 2x arctg3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Воспользуемся правилами и формулам нахождения производной:
- производная сложной функции ( f (u(x))) |
|
|
f |
|
|
|
(u(x)) u (x) |
||||
-производная суммы 2-х функций u v
-производная произведения 2-х функций
u v |
|
|
u v u v |
u v |
|
- формулами
|
|
1 |
|
|
1 |
|
arcsin x |
|
arctgx |
1 x |
2 |
||
|
|
1 x |
2 |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin 2x |
x arcsin 2x arctg3x |
x arcsin 2x x arcsin 2x |
arctg3x |
||||||||||||||
|
|
2x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
9x2 |
|
|
|
|
|
|
|
|
|||
1 4x2 |
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
в) y 5 |
sin 2 x |
|
3 |
x |
tg 2x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Воспользуемся правилами и формулам нахождения производной: |
||||||||||||||
|
|
- производная сложной функции ( f (u(x))) |
|
f |
|
|
|
|||||||||
|
|
|
(u(x)) u (x) |
|
||||||||||||
-производная суммы 2-х функций |
|
u v |
- производная произведения 2-х функций
u v |
|
|
u v u v |
u v |
|
|
|
|
x |
|
х |
|
|
|
1 |
|
|
|
|
- формулами |
(а |
|
) а |
|
ln a |
; tgx |
|
|
|
; sin x |
cosx ; |
|
|
|
cos2 |
|
||||||||
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
x |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
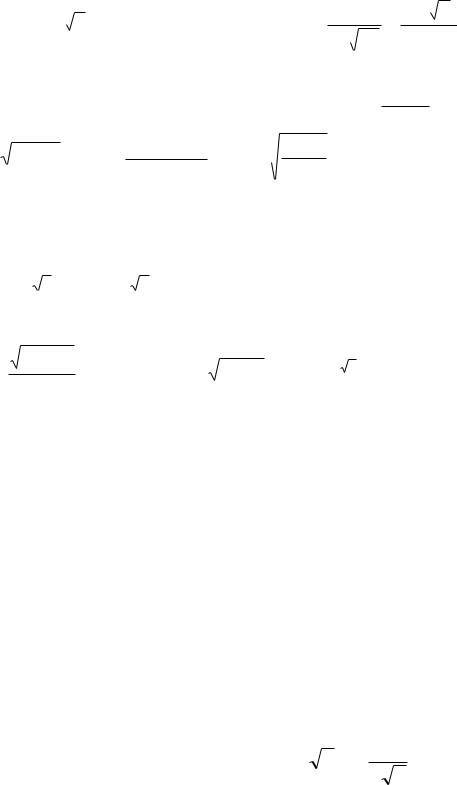
у 5 |
sin 2 x |
|
3 |
|
|
|
|
|
|
|
|
sin 2 x |
|
|
|
|
tg 2x |
|||||||||
|
x |
tg 2x |
5 |
ln 5 2cos2x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
3 |
3 |
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите самостоятельно: |
|
|
|
|
|||||||||
|
4 |
|
|
|
|
|
|
|
x |
5 |
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
||
а) у 3х |
cos2x |
e |
|
б) |
y x arcsin x e |
в) y |
ln |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
sin x 5x |
4 |
|
|
x 2 |
|
|
|
|
|||||
г) y arctg |
x |
4 |
|
д) |
y |
|
е) |
y |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
3x 5 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
3 |
x |
|
|
|
|
|
|
2 |
2x |
|
|
||
|
cos |
||
x2 4
2x 3
;
Задания для самосоятельного решения:
1. Составить уравнения касательной и нормали
астроиде |
x |
2 cos |
3 |
t; y |
2 sin |
3 |
t |
, проведенной в |
|
|
|||||||
|
|
|
|
|
|
|
2) Найти производную функции
к
точке, для которой t= /4.
а)
|
1 5х |
2 |
||
у |
|
|||
2 5х |
2 |
|||
|
||||
|
|
|
||
б)
y ln |
4 |
(x |
2 |
|
x |
4 |
1) |
|
|
|
в)
y 3 |
x |
x |
2 |
tg3x |
|
|
Дифференцирование сложной, обратной, показательно-степенной функции
1.Дифференцирование сложной функции.
2. Дифференцирование обратной функции.
2. Логарифмическая производная.
Теоретическая часть:
Пусть переменная у есть функция от переменной u(y=f(u)), а переменная u в свою очередь есть функция от независимой переменной х: u=z(x). Тогда у называется функцией от функции или сложной функцией y=f(z(x)).
Производная сложной функции y=f(z(x)) находится по правилу:
y'
f |
' |
|
z |
||
|
z
' |
|
|
|
|
|
|
|
x . |
|
|
|
|
|
|
|
|
x |
k |
/ |
k x |
k 1 |
||
1) |
|
|
|
||||
|
|
|
|
|
|
|
|
3) |
ln x / |
1 |
|
|
|||
x |
|
||||||
|
ex / |
|
|
||||
5) |
ex |
|
|||||
7) |
cos x / sin x |
||||||
|
|
x |
|
|
|
|
1 |
|
|
|
|
2) |
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
||||
|
a |
|
|
|
|
|
|||||
|
|
/ |
a |
|
ln a |
||||||
4) |
x |
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
6) |
sin x / |
cos x |
|||||||||
|
|
|
/ |
|
|
|
|
1 |
|
|
|
8) |
tgx |
|
|
|
|
|
|
|
|
||
|
cos |
2 |
x |
||||||||
|
|
|
|
|
|
|
|||||
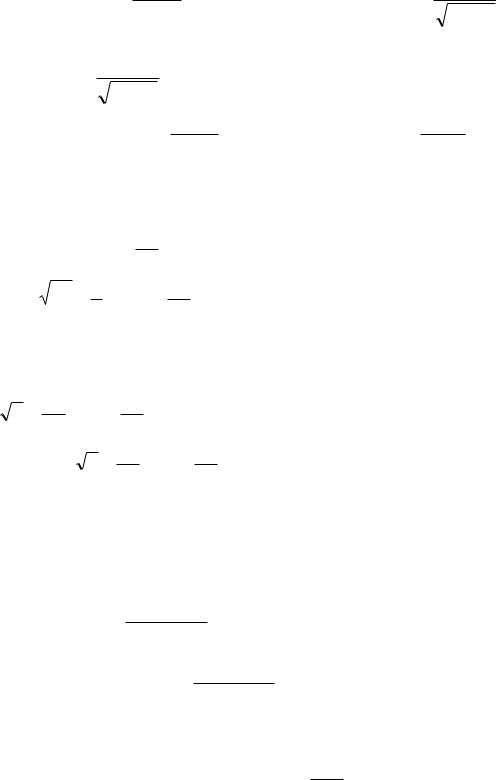
|
|
|
/ |
|
1 |
|
|
|
9) |
ctgx |
sin |
2 |
x |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
11) |
|
|
|
|
|
|
|
|
|
|
/ |
|
1 |
|
|
|
|
arccos x |
1 x |
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
/ |
|
1 |
|
|
13) |
arcctgx |
1 x |
2 |
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
1 |
|
|
10) |
arcsin x |
1 x |
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
12) |
arctgx / |
|
|
1 |
|
|||
|
2 |
|
||||||
|
|
|
|
|
1 |
x |
||
|
log |
|
/ |
|
|
|
1 |
|
14) |
a |
x |
x ln a |
|||||
|
|
|
||||||
|
|
|
|
|
||||
Практическая часть:
1. Найти производные
dy dx
функций, заданных в явном виде.
|
|
|
3 |
|
7 |
|
2 |
2 |
|
а) |
y 2 |
x |
|
|
3x |
. |
|||
|
|
|
|||||||
|
|
|
|
x |
|
|
x |
5 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Предварительно запишем функцию в виде, удобном для дифференцирования
у=2x3/2-7x-1+3x2-2x-5, тогда у=3x1/2+7x-2+6х+10x-6=
= |
3 |
x |
7 |
6х |
||
|
2 |
|||||
|
|
x |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
Ответ: |
у' 3 |
x |
||||
|
|
|
|
|||
б) у=e-xtg(7x6). y =( e-x) tg(7x6)+
= e x ( x)' tg(7x
10 |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
x |
6 |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
7 |
6х |
10 |
. |
|
|
|
||||
|
2 |
|
6 |
|
|
|
||||
x |
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
e-x( tg(7x6))= |
|
|
|
|||||||
6 ) e x |
|
|
|
1 |
(7x |
6 )' |
||||
|
|
|
|
|||||||
cos2 |
(7x 6 ) |
|||||||||
|
|
|
|
|
|
|||||
|
x |
|
6 |
|
42x |
5 |
e |
x |
|
||||
e |
tg(7x |
) |
|
|
|
|
|
. |
|||||
|
|
|
2 |
|
|
|
6 |
|
|||||
|
|
|
|
|
cos |
(7x |
) |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Ответ:
|
x |
|
6 |
|
42x |
5 |
e |
x |
|
||||
y' e |
tg(7x |
) |
|
|
|
|
|
. |
|||||
|
|
|
2 |
|
|
|
6 |
|
|||||
|
|
|
|
|
cos |
(7x |
) |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
в) y=arctg2(5x)ln(x-4). y =(arctg2(5x))ln(x-4)+
=2arctg(5x)( arctg(5x))
arctg2(5x)( ln(x-4))=
ln(x-4)+arctg2(5x) |
1 |
|
х 4 |
||
|
(x-4)=
2arctg(5x) |
|
1 |
(5x)' ln( x 4) |
arctg 2 (5x) |
|
|
(5x)2 |
x 4 |
|||
1 |
|
|
|||
|
10arctg(5x) ln( x 4) |
|
arctg 2 |
(5x) |
. |
|||
1 |
25x |
2 |
x |
4 |
||||
|
|
|
||||||
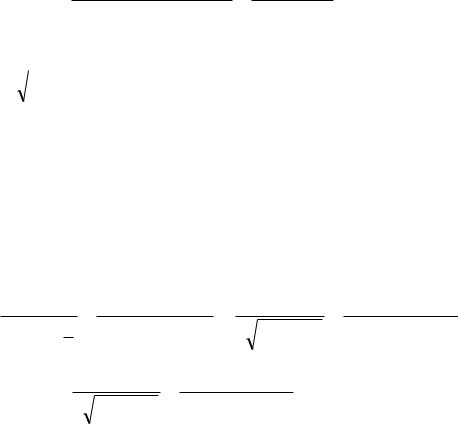
Ответ:
г)
|
10arctg(5x) ln( x 4) |
|
arctg |
2 |
(5x) |
|
||
y' |
|
|
. |
|||||
1 25x |
2 |
x 4 |
||||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||
y 5 (x 4)3 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
(x 4) 5 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx |
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
|
|
|
3 |
1 |
(x)' tgx x(tgx )' |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y' |
|
(x 4) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
(x 4) 2 / 5 |
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
tgx |
cos |
2 |
x x |
|
|
|
|
|
|
|
3 |
|
|
|
sin x cos x x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
x cos |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
tg |
x |
|
|
|
|
|
5 |
(x |
|
4) |
2 |
sin |
x |
|
||||||||||||||||||||
|
5(x 4) 5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: |
y' |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
sin x cos x x |
. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
5 |
(x 4) |
|
|
|
|
|
|
sin |
x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
д) |
y sin |
3 |
(cos |
2 |
(x e |
3x |
)). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' |
3sin |
2 |
(cos |
2 |
(x |
e |
3x |
)) |
(sin(cos |
2 |
(x e |
3x |
))' |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
3sin 2 (cos 2 (x e3x )) cos(cos 2 (x e3x ))
(cos 2 (x e3x ))' 3sin 2 (cos 2 (x e3x )) cos(cos 2 (x e3x ))
2 cos(x e3x ) (cos(x e3x ))' 6 sin 2 (cos 2 (x e3x ))
cos(cos 2 (x e3x )) cos(x e3x ) ( sin( x e3x )) (x e3x )'
6sin 2 (cos 2 (x e3x )) cos(cos 2 (x e3x )) cos(x e3x )
sin( x e3x ) (e3x xe 3x 3).
Ответ:
y' 6sin |
2 |
(cos |
2 |
(x e |
3x |
)) cos(cos |
2 |
(x e |
3x |
)) cos(x e |
3x |
) sin( x e |
3x |
) e |
3x |
(3x |
1). |
|
|
|
|
|
|
|
|
Применим метод логарифмического дифференцирования. Прологарифмируем обе части.
lny=cosx ln(tgx).
Продифференцируем обе части по х
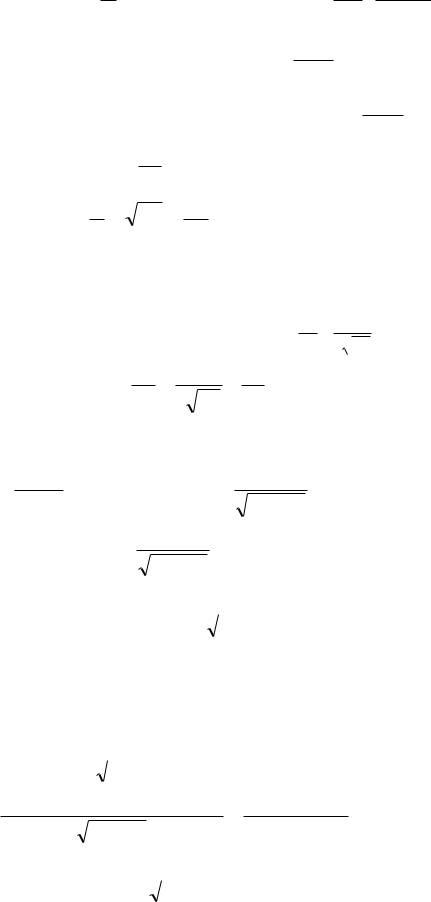
y' |
sin x ln( tgx ) cos x |
1 |
|
1 |
; |
||||||
y |
tgx |
|
2 |
||||||||
|
|
|
|
|
|
|
cos |
x |
|||
|
|
|
|
|
|
|
|
||||
y' y( sin x ln( tgx ) |
1 |
); |
|
|
|
|
|||||
sin x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y' |
(tgx ) |
cos x |
( sin x ln( tgx ) |
|
1 |
). |
|
||||
|
|
|
|||||||||
|
sin x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
dy |
|
|
|
|
|
|
|
|
|
2. Найти производные |
dx |
функций, заданных в явном виде. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y 4x |
3 |
|
3 |
|
5 |
x |
2 |
|
6 |
|
а) |
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Предварительно запишем функцию дифференцирования
у=4х3-3х-1-х2/5+6х-2,
тогда у =12x2+3x-2-2/5x-3/5-12x-3= 12x |
2 |
|
3 |
|
|
2 |
|||
|
|
|
x |
|
в виде,
2 12x 3
55 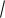 x3
x3
удобном для
.
Ответ:
y' 12x |
2 |
|
3 |
|
2 |
|
12 |
. |
||
|
|
|
|
|
||||||
|
x |
2 |
|
x |
3 |
|||||
|
|
|
5 |
x |
3 |
|
||||
|
|
|
|
|
5 |
|
|
|
|
|
б) у=ctgx arccos(2x3). y =(ctgx) arccos(2x3)+ctgx (arccos(2x3)) =
= |
|
|
1 |
arccos(2x |
3 |
) ctgx |
1 |
(2x |
3 |
)' |
|
|
|
|
||||||
|
2 |
|
|
|
||||
sin |
x |
|
|
1 4x |
6 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
arccos(2x |
3 |
) |
|
6x |
2 |
ctgx |
|
|||
|
|
|
|
. |
|||||||
sin |
2 |
x |
|
|
1 4x |
6 |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: y = |
arccos(2x 3 ) |
|
6x 2 ctgx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
sin |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
в) y=arcsin5(2x) log2(3x+5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y =( arcsin5(2x)) log2(3x+5)+arcsin5(2x) (log2(3x+5)) = |
|
|
|
|
|||||||||||||||||||||||||||||||||||
=5 arcsin4(2x) (arcsin(2x)) log2(3x+5)+arcsin5(2x) |
|
1 |
|
3= |
|||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
3х |
5 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 arcsin 4 (2x) |
|
|
1 |
|
|
|
|
|
(2x)' log |
|
(3x 5) |
3arcsin 5 (2x) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 4x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
5 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
10 arcsin |
4 |
(2x) |
log |
|
(3x 5) |
|
|
|
3arcsin |
5 |
(2x) |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
1 4x |
|
|
|
|
|
|
|
|
|
|
|
|
3x 5 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: y' |
10 arcsin 4 (2x) log |
2 |
(3x 5) |
|
|
3arcsin 5 (2x) |
. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
5 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 4x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

|
|
|
|
3 |
(x |
1) |
7 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
y |
|
|
|
|
|
|
|
(x 2) |
7 / 3 |
(x 1) |
5 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(x |
|
1) |
5 |
sin x |
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
7 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2x sin x x |
2 |
cos x |
|
||||||||
y' |
(x 1) |
3 |
(x |
1) |
5 |
(x 1) |
3 |
( 5(x 1) |
6 |
) |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x sin x x |
2 |
cos x |
|
|
||||||||||||
|
(x 1) |
3 |
(x 1) |
6 |
[7(x 1) 15(x |
1)] |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 1) |
3 |
(22 8x) |
|
|
|
|
2x sin x x |
2 |
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3(x 1) |
6 |
|
|
|
|
|
sin |
2 |
|
x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 1) |
3 |
(22 8x) |
|
2x sin x x |
2 |
cos x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
|
|
3(x 1) |
6 |
|
|
|
|
|
|
sin |
2 |
x |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: у=
sin( 2sin xctgx ) cos |
|
xctgx |
(x cos x sin x) |
. |
||
2sin |
2 |
x |
xctgx |
|||
|
||||||
|
|
|||||
д) y=(sinx)arcsinx.
Применим метод логарифмического дифференцирования. Прологарифмируем обе части.
lny=arcsinx lnsinx.
Продифференцируем обе части по х
|
|
|
|
|
y' |
|
|
|
1 |
|
|
ln sin x arcsin x |
|
1 |
cos x; |
|
|
||||||||||||
|
|
|
|
|
y |
1 x |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
sin x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' y( |
|
ln sin x |
ctgx arcsin x); |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' (sin x) |
arcsin x |
( |
ln sin x |
ctgx |
arcsin x). |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 x |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
y' (sin x)arcsin x ( |
ln sin x |
|
|
ctgx arcsin x). |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Найти производные указанного порядка |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
у=xln(1+3x) |
|
|
у=?. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
||||
y =ln(1+3x)+x |
|
1 |
|
|
3 |
|
ln(1 |
|
3x) |
3x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
3х |
|
|
|
|
|
|
|
|
|
|
|
|
1 3x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y" |
3 |
|
3(1 3x) 3x 3 |
|
3 9x 3 9x 9x |
|
6 9x |
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
||||||
1 3x |
|
|
(1 3x) |
|
|
|
|
|
|
|
|
|
(1 3x) |
|
|
(1 3x) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: y' ' |
6 9x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(1 3x) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Найти производную |
|
|
y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
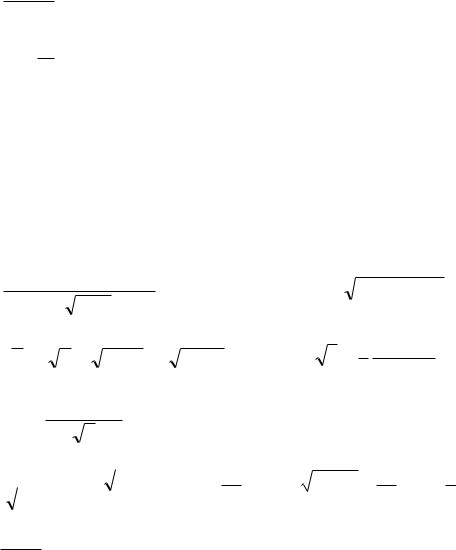
|
|
|
3t |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3t |
3 |
|
, |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
1. |
|
|
|
|
t |
|
||
|
y sin |
|
|
3 |
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
x cos 2t, |
|
||
2. |
|
2 |
|
|
y 2sec |
t. |
|||
|
|
|||
t |
|
. |
|
|
|
|
|
. |
|
Задания для самосоятельного решения:
1.Найти производную.
1). |
y |
|
|
3) |
y |
|
|
5) |
y |
|
2(3x |
3 |
|

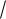 x ln(
x ln(
arctg
|
4x |
2 |
x 2) |
|
||
|
. |
|||||
15 |
1 |
x |
|
|
||
|
|
|
||||
x |
x a ) |
|||||
tgx ctgx |
. |
6) |
y |
|||
|
|
2 |
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
2) |
y x ln( 2 e |
x |
2 |
e |
2 x |
e |
x |
1. |
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
sin |
2 |
3x |
|
||||
x a. |
4) |
y sin |
3 |
|
. |
|||||||||||
3 3cos 6x |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
(arctgx) |
(1/ 2) ln arctgx |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
arcsin |
x |
|
|
|
|
1 |
|
|
4 x |
4 |
|
2 |
|
||||
7) y |
ln 1 x2 . |
8) y |
(x2 8) |
x2 |
arcsin |
, |
||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
24 |
|
x |
||||||||||||
|
|
|||||||||||||||||||
|
|
1 x |
|
|
|
|
|
|
|
16 |
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8) |
y |
1 |
|
ln( tgx ctg ). |
|
|
|
|
|
|
|
|
|
|
||||||
sin |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. Показать, что функция y удовлетворяет данному уравнению. |
|
|||||||||||||||||||
|
y xe |
x |
2 |
/ 2 |
. xy (1 x |
2 |
) y. |
|
|
|
|
|
|
|
|
|||||
1. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 0.
Неявная функция, ее дифференцирование. Дифференциал функции, его свойства
1.Дифференцирование неявной функции
2.Дифференциал функции в точке, его геометрический смысл.
3.Приближенные вычисления с помощью дифференциалов.
Теоретическая часть:
Дифференциал функцииdy есть главная часть ее приращения у, линейная относительно х с коэффициентом пропорциональности равным производной f'(x).
порядка —
d |
3 |
y |
|
||
dx |
3 |
|
|
||
, и т.д.
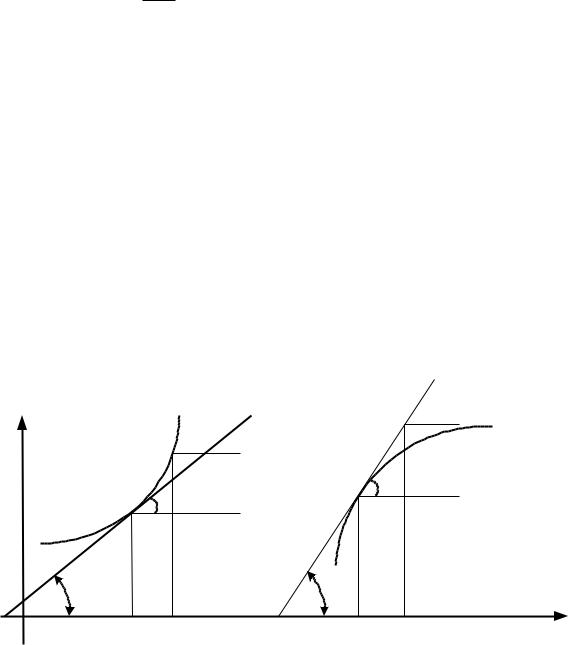
Геометрическое представление дифференциала
Возьмем на графике функции y=f(x)точку с фиксированной абсциссой х=ОА, тогда у=АС (на рис.10 показаны два случая; буквенные обозначения для них одни и те же). Дадим аргументу приращение x=AB=CD. Тогда приращение функции будет y=DM. Проведем теперь касательную к кривой в точке С (х; у). Тангенс ее угла наклона α равен производной в той же точке: y′ = tgα (7)
Из прямоугольного треугольника CDEмы видим, что DE=CD ∙ tga=
х·у'
В правой части мы получили выражение дифференциала функции dy, следовательно, dy=DE.
Таким образом, если при некотором х приращение функции у в некоторой точке хесть приращение ординаты ее графика (DM), то дифференциал функции dyравен приращению ординаты касательной к графику в точке (х; у) при том же значении х.
|
|
|
|
I |
|
|
|
|
II |
|
E |
|
|
y |
|
|
|
|
|
|
|
|
|
|
y=f(x) |
||
|
|
|
|
|
|
|
|
|
|
M |
|
||
|
|
|
|
|
M |
|
|
|
|
|
} |
||
|
|
|
|
|
|
y |
|
|
} |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
E |
} |
|
|
|
|
y |
dy |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
C |
|
}dy |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
x |
D |
|
|
|||
|
|
|
|
) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
|
x |
x |
|
|
|
|
|
|
|
|
|
|
f( |
|
D |
|
|
|
|
|
|
|
|||
|
= |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
A |
|
B |
|
|
0 |
|
|
|
x x |
|
|
|
x |
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из рисунка мы видим, что dуможет быть и меньше, чем у (1) и больше (II). Разность между у и dyравна отрезку ЕМ.
Тот факт, что при небольших значениях х дифференциал функции приближенно равен ее приращению: у≈dу, позволяет во многих случаях заменять с достаточной точностью величину у, вычисление которой иногда бывает весьма затруднительным или громоздким, величиной dy, которую можно вычислить гораздо легче.
В этом и заключается принцип применения дифференциала к приближенным вычислениям. Схема этого метода такова. Требуется найти численное значение некоторой функции y=f(x) при таком значении

аргумента, при котором вычисление у затруднительно. Тогда, если х оказывается весьма близким к некоторому другому значению аргумента х0(х=х0+ х), при котором значение функции у0 [y0=f(x0)] найти легко, то вместо искомого значения функции y=y0+ y=f(x0+ x) находим ее приближенное значение: у ≈ y0+f’ (х0)· х
Практическая часть:
1.Найти производные указанного порядка
у=(5-х2) ln2x у =?.
Решение: y =(5-x2) ln2x+(5-x2) ( ln2x) =-2x ln2x+(5-x2) 2lnx (lnx) =
=-2x ln2x+(5-x2) 2lnx |
1 |
=2(5x-1-x)lnx-2x ln2x |
|||||||||||||
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y =2(-5x-2-1)lnx+2(5x-1-x) |
1 |
-2 ln2x-2x 2lnx |
1 |
||||||||||||
x |
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2ln2x= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10(1 ln x) |
6 ln x 2 2 ln |
2 |
x. |
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: y'' |
|
10(1 ln x) |
6 ln x 2 2 ln |
2 |
x. |
||||||||||
|
|
|
|
||||||||||||
|
|
2 |
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=(-10x-2-6) lnx+10x-2-2-
2. Найти первую и вторую производные неявной функции и функции,
заданной параметрически. |
|
а) y=ey+4x. (условие изменено) |
|
Продифференцируем обе части по х |
|
y'=ey y'+4; y'(1-ey)=4; |
(*) |
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
y' |
|
4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дифференцируем равенство (*) по х |
|
|
|
|
|
|
|||||||||||||
y'' (1-ey)+y' (-ey) y =0. Отсюда |
|
|
|
|
|
|
|
|
|||||||||||
|
e |
y |
(y') |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y'' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 e |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя вместо у |
его выражение, получим |
y'' |
16e y |
. |
|||||||||||||||
(1 |
e y )3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
|
y' |
|
4 |
|
. y' ' |
16e y |
|
. |
|
|
|
|
|
|
||||
|
|
e y |
|
(1 e y )3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
x 
 t
t
б) y 3 t 1
Первую и вторую производные найдем по формулам
