
Практикум по математическому анализу
.pdfТеоретическая часть:
1. Понятие об определенном интеграле
Пусть f(x) – функция, непрерывная на данном отрезке [a, a>b, и F(x) – некоторая ее первообразная, т.е. F`(x)=f(x) при х
Определение. Под определенным интегралом
b], где a<b или
[a,b].
b f (x)dx
a
(1)
от данной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение ее первообразной, т.е.
b f (x)dx F (b) F (a)
a
(2)
(формула Ньютона-Лейбница).
В выражение (1) числа a и b называются пределами интегрирования, соответственно - нижним и верхним, [a, b] – промежутком интегрирования, а f(x) – подынтегральной функцией. Формулу (2) можно выразить в виде правила: определенный интеграл равен разности значений первообразной
подынтегральной функции для верхнего и нижнего пределов интегрирования.
Теорема: Определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции.
Теорема: Для всякой функции, непрерывной на отрезке [a,b] существует соответствующий определенный интеграл.
2. Определенный интеграл с переменным верхним пределом
Пусть функция f(x) непрерывна на отрезке [a,b]. Рассмотрим интеграл
x
a
f (t)dt
,
(1)
где t [a,x] [a,b] (во избежание путаницы, переменная интегрирования обозначена другой буквой).
Если F(x) – первообразная функции f(x), т.е.
F`(x)=f(x),
то согласно формуле Ньютона-Лейбница имеем
|
|
|
|
|
x |
|
|
|
|
|
|
|
f (t)dt F (x) F (a) . |
(2) |
|
|
|
|
|
|
a |
|
|
Отсюда |
|
|
|
|
|
||
|
d x |
|
d |
|
|
|
|
|
|
|
f (t)dt |
|
F (x) F (a) F (x) F (a) |
f (x) 0 |
f (x) . |
|
dx |
dx |
|||||
|
|
a |
|
|
|
|
|

Следовательно, производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции для этого предела:
d |
x |
|
f (t)dt |
||
dx |
||
a |
||
|
f
(x)
.
(3)
Таким образом, интеграл
x Ф(x) f (t)dt
a
(4)
является первообразной для подынтегральной функции f(x). Отметим, что из формулы (2) следует, что Ф. (а)=0, т.е. Ф. (х) есть та первообразная для функции f(x), которая обращается в нуль при х=а.
На основании формулу Ньютона-Лейбница имеем
d |
|
|
b |
|
|
dx x |
|
|
|
f (x)dx |
|
|
|
d |
|
dx |
F(b) E(x) F(b) |
|
F (x)
f
(x)
.
Таким образом, производная определенного интеграла с переменным нижним пределом по этому пределу равна значению подынтегральной функции для этого предела, взятому с обратным знаком.
Интегрирование по частям в определенном интеграле
Пусть u=u(x), υ=υ(х) – непрерывно дифференцируемые функции т.е. имеющие непрерывные производные u`(x), υ`(x) на отрезке [a,b].
Имеем:
d u(x) (x) (x)du(x) u(x)d (x) .
Интегрируя это равенство в пределах от a до b и учитывая, что
du(x) u (x)dx |
и |
d (x) (x)dx |
, |
||
|
|
|
|
||
находим |
|
|
|
||
|
|
b |
|
b |
|
u(x) (x) |
|
ba (x)u (x)dx u(x) (x)dx . |
|||
|
|||||
|
|||||
|
|
a |
|
a |
|
Отсюда получаем формулу интегрирования по частям в определенном интеграле
b u(x) (x)dx
a
u(b) (b) u(a) (a)
b (x)u (x)dx
a
.
Для краткости употребляется
u(b) (b)
(1)
обозначение
u(a) (a) u(x) (x) |
b |
, |
|
a |
|||
|
|||
|
|
Замена переменной в определенном интеграле
Пусть дан определенный интеграл
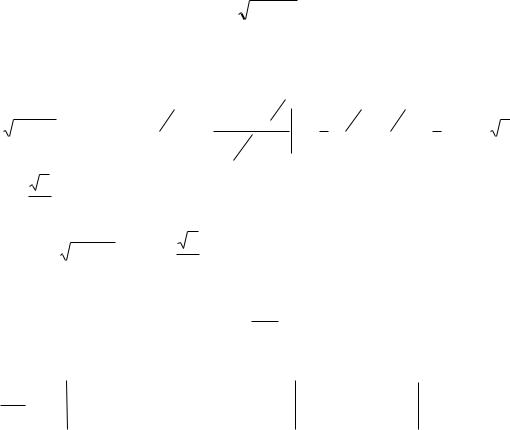
b
a
f
(x)dx
,
(1)
Где f(x) – непрерывная функция на отрезке [a,b], и пусть по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней х соотношением:
х=φ(t ) (α ≤ t ≤ β), |
(2) |
где φ(t ) – непрерывно дифференцируемая функция на отрезке [a,b]. Если при этом: 1) при изменении t от α до β переменная х меняется от a до b,
т.е. |
|
φ(α)=а, φ(β ) = b, |
(3) |
и 2) сложная функция f(φ(t)) определена и непрерывна на отрезке [α,β] (если значения φ(t) не выходят из отрезка [a,b], то условие 2) излишне – теорема о непрерывности сложной функции), то справедлива формула
b |
|
|
|
. |
|
f (x)dx |
|
f( (t)) (t)dt |
|
|
|
|
||
a |
|
|
|
|
Практическая часть:
(4)
1. Вычислите определенные интегралы.
а)
1 |
|
|
|
|
|
3 |
6x |
2dx |
|
||
0 |
|
|
Решение:
1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
(6x 2) |
3 1 |
|
1 |
|
|
1 |
3 |
|
|||||
6x |
|
2dx |
(6x 2) |
3 dx |
|
|
|
|
|
|
(8 |
3 |
2 |
3 ) |
|
2) |
||||||
|
4 |
|
6 |
0 |
8 |
8 |
(16 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
1,685. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ:
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||
|
3 |
6x |
2dx |
2 |
|
2 |
1,685. |
|
|
|
|||||
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
12х
b)0 ех2 dx
Решение:
1 |
2х |
|
|
x |
2 |
u; Если х 0, то u 0; |
1 |
|
|
|
1 |
|
|
|
|||
|
dx |
|
e |
u |
du e |
u |
1 e |
1 |
0,632. |
||||||||
|
|
|
|
|
|
|
|
||||||||||
е |
х |
2 |
2хdx du; Если х 1, то |
u 1; |
|
|
0 |
|
|||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
2х |
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
dx 1 e 1 0,632. |
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
ех |
|
|
|
|
|
|
|
|
|
|
|
|
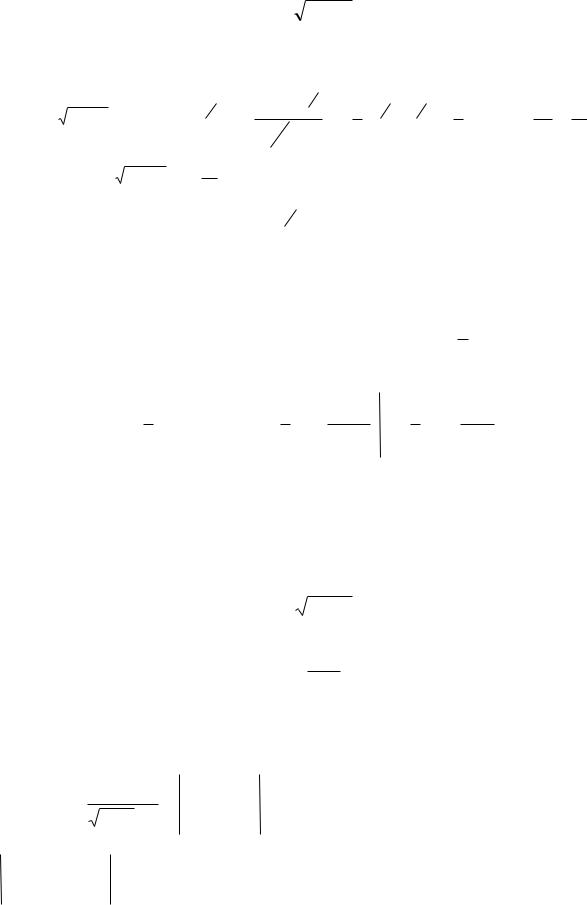
Вычислите определенные интегралы.
|
2 |
|
c) |
|
4х 1dx |
|
|
|
|
0 |
|
Решение:
2 |
|
|
2 |
|
|
|
|
|
(4x 1) |
3 |
2 |
|
|
|
|||
|
|
|
|
1 |
|
|
2 |
|
1 |
|
|||||||
|
4х 1dx (4x 1) |
|
dx |
|
(9 |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
3 |
2 |
4 |
|
0 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
|
4х 1dx |
|
. |
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
2xdx |
|||||
|
|
|
|
|
|
|
|
|
d) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Решение:
Воспользуемся тригонометрической формулой
|
|
|
|
|
4 |
|
|
|
|
соs |
2 |
2xdx |
||
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
Ответ: |
|
соs |
||
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
1 |
|
sin 4x |
|||
(1 |
cos |
4x)dx |
|||||||||
|
|
|
x |
|
|
||||||
2 |
0 |
|
|
|
|
2 |
|
4 |
|
||
|
|
|
|
|
|
|
|
|
|
||
2 |
2xdx |
|
|
0,393. |
|
|
|
||||
|
|
|
|
||||||||
|
8 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
3 |
2 |
1 |
3 |
2 |
) |
1 |
(27 |
1) |
|
26 |
|
13 |
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
6 |
|
|
|
6 |
|
3 |
|
соs |
2 |
2x |
1 |
(1 cos 4x) |
|
|||||||||
|
|
|||||||||||||
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
sin |
|
|
|
|
||||
4 |
|
|
0 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|||||||
0 |
|
2 |
|
4 |
|
|
4 |
|
|
|
8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Вычислите определенные интегралы.
а)
2 |
|
|
5x 1dx |
1 |
|
|
e |
b) |
|
|
1 |
ln |
2 |
x |
|
|
dx |
||
x |
|
||
|
|
||
3. Вычислить определенные интегралы: а) по формуле Ньютона-Лейбница;
б) по формуле Симпсона при n=10 с точностью до двух знаков.
а)
7 |
|
|
x 1 t |
3 |
3 |
dx |
|
||
|
|
|||
x 1 1 |
2 |
|||
|
|
|
||
0 |
|
dx 3t dt |
||
|
|
|
|
|
= Найдем новые пределы интегрирования
x 0 t 1 |
2 |
3t 2dt |
2 |
(t 2 |
|
2 |
|
|
|
|
|
1) 1 |
1 |
|
|||||
x 7 t 2 = |
|
3 |
|
|
dt 3 (t 1 |
|
|
)dt |
|
t 1 |
|
t 1 |
t 1 |
||||||
1 |
1 |
1 |

|
t |
2 |
t ln | t 1 |) |2 |
|
|
|
1 |
|
|
|
3( |
|
3(2 |
2 ln 3) |
3( |
1 |
ln 2) |
1,5 3ln 3 3ln 2 |
|||
|
|
|
||||||||
|
2 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1,5 3ln 1,5 2,716 |
|
|
|
|
|
|
|
|||
Ответ:
7 |
|
|
|
|
3 |
dx |
1,5 |
3ln 1,5 |
2,716 |
|
||||
|
x 1 1 |
|||
0 |
|
|
|
|
|
|
|
|
б)
11 |
|
|
|
|
x |
3 |
32dx |
|
|||
|
|
||
1 |
|
|
|
Применим приближенную формулу Симпсона
b |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
h |
(y |
|
y |
|
|
4(y |
y |
|
|
... y |
n 1 |
) 2(у |
|
у |
|
у |
n 2 |
)) |
|||
|
|
0 |
n |
3 |
2 |
4 |
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
h=(b-a)/n, |
(n-четное число, у нас n=10), |
yi |
значения |
|||||||||||||||||||
подынтегральной функции в точках xi=a+ih. |
|
|
|
|
|
|
|
|
|||||||||||||||
В нашем случае |
h |
11 1 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заполним таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xi |
|
|
|
yi= |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i |
|
|
|
|
xi 32 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
1 |
|
|
|
|
|
|
5,74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
6,32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
7,68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
|
|
|
|
|
9,80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
|
|
|
|
|
12,53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
|
|
|
|
|
15,75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
7 |
|
|
|
|
|
19,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
8 |
|
|
|
|
|
23,32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
9 |
|
|
|
|
|
27,59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
10 |
|
|
|
|
|
32,12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
11 |
|
|
|
|
|
36,92 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находим: у0+у10=5,74+36,92=42,66. у1+у3+у5+у7+у9=6,32+9,80+15,75+23,32+32,12=87,32. 4 87,32=349,28. у2+у4+у6+у8=7,68+12,53+19,36+27,59=67,16. 2 67,16=34,32.
11 |
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
||
|
x |
3 |
32dx |
|
1 |
(42,66 349,28 134,32) |
1 |
526,26 175,42 |
|
|
|
||||||
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
Задания для самосоятельного решения:
1. Вычислить определенные интегралы:

а) по формуле Ньютона-Лейбница;
б) по формуле Симпсона при n=10 с точностью до двух знаков.
6 |
x 3 |
8 |
|
|
а) |
|
|
||
x |
dx ; б) |
82 x2 dx |
||
3 |
|
2 |
|
|
|
|
|
|
|
Применение определенного интеграла к вычислению площадей плоских фигур
1.Вычисление площади плоской фигуры в ПДСК.
2. Вычисление площади плоской фигуры в полярной системе координат
Теоретическая часть:
При решении этих задач полезно придерживаться следующего порядка.
1.Сделать чертеж фигуры (дуги), описываемой уравнениями, заданными в задаче.
2.Выбрать подходящую формулу.
Y
Y
Р
В декартовой системе координат (рис. 1):
b S ( f2 (x) f1 (x))dx. a
r
r
Р
(1)
В полярной системе координат (рис. 2):
S1 (r22 ( ) r12 ( ))d . 2
(2)

b
Р
При
параметрическом задании
кривой (рис.3):
|
T |
|
|
S |
|
y(t)x (t)dt. |
(3) |
|
|
||
|
t |
|
|
|
0 |
|
|
Замечание: Если кривая f(x) задана параметрически или в полярной системе координат, то в определенном интеграле надо сделать замену переменных. Не забудьте про новые пределы интегрирования!
Практическая часть:
1. Найдите площадь фигуры, ограниченной линиями. y=x2-4 и y=4-x2.
Решение: Обе линии являются параболами.
Вершина первой параболы находится в точке (0; -4). Ветви направлены вверх.
Вершина второй параболы находится в точке (0; 4). Ветви направлены
вниз.
Найдем точки пересечения этих линий.
y x 2 |
4 |
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
x |
4 |
4 x |
, 2x |
8, |
x |
4, |
||||||
|
|
|
|
|
|
|||||||||
y 4 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1,2 2, x1 2, x 2 2, y1 0, y2 0. |
|
|
|
|||||||||||
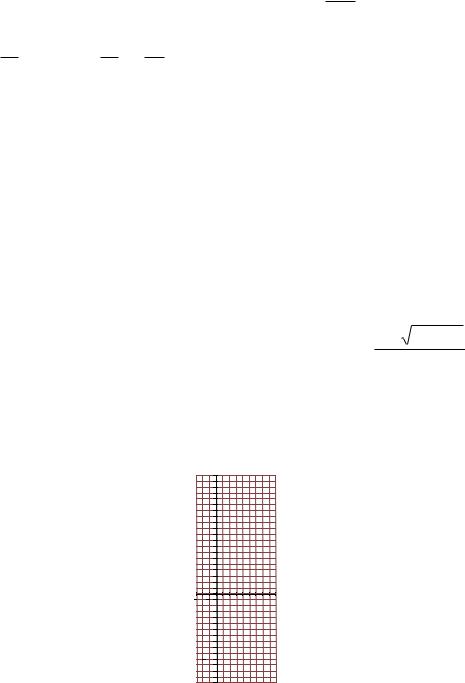
Сделаем чертеж: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
5 |
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
у=4-х2 |
|
||
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
2 |
1 |
1 |
0 |
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
у=х2-4 |
|
||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
х
Площадь найдем по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
[f |
2 |
(x) f |
(x)]dx |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2x |
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
S |
|
[(4 |
x 2 ) (x 2 |
4)]dx |
|
|
(8 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2x 2 )dx 8х |
3 |
|
|
|
2 |
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
16 |
|
|
16 |
|
16 |
|
64 |
(кв.ед.). |
|
|
|
|
|
|
|
|||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
3 |
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Искомая площадь 64/3 (кв. ед.).
2. Найдите площадь фигуры, ограниченной линиями. y=x2-5x-6 и y=x+10.
Решение:
Первая линия является параболой, вторая - прямой. Для построения параболы преобразуем ее уравнение: у=х2-2 2,5 х+2,52-2,52-6; у=(х-2,5)2-
12,25; у+12,25=(х-2,5)2.
Из последнего уравнения следует, что вершина параболы находится в
точке
(2,5; -12,25), а ось симметрии параллельна оси Оy. Найдем точки пересечения этих линий
y x |
2 |
5x 6 |
|
|
|
|
|
|
|
|
|
|
6 |
36 64 |
|
|
x |
2 |
5x 6 |
x 10, |
x |
2 |
6x 16 |
0, |
x |
|
, |
||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||
10 |
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
||
y x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
x1=-2, x2=8, y1=8, y2=18.
Сделаем чертеж:
20
19
 18
18
17
16
 15
15  14
14
13
 12
12
11 10
9
8
7
6
5
4
3
2
1
3 2 11 0 1 2 3 4 5 6 7 8 9
2 11 0 1 2 3 4 5 6 7 8 9 
 2
2 


 3
3

 4
4

 5
5 
 6
6

 7
7

 8
8 
 9
9
 10 11
10 11  12
12  13
13
 14
14  15
15
b
Площадь найдем по формуле S [f2 (x) f1(x)]dx
a

|
8 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
x |
3 |
8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
[x 10 |
x 2 |
5x 6]dx |
|
|
(6x 16 |
x 2 )dx 3x |
2 |
16x |
3 |
|
2 |
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
512 |
|
|
32 |
|
8 |
|
340 |
|
520 |
166 |
2 |
(кв.ед.). |
|
|
|
|
|
||||
192 128 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
Ответ: Искомая площадь 166 2/3 (кв. ед.).
3.Вычислить площадь фигуры, ограниченной кардиоидой
r 3(1 cos ).
Решение Сделаем чертеж
|
90 |
135 |
45 |
180 |
|
|
0 |
0 2 |
4 |
6 |
8 |
225 |
|
315 |
|
270 |
|
|
|
Площадь фигуры в полярной системе координат найдем по формуле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
1 |
|
r |
2 |
( )d . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S |
1 |
|
(1 cos ) |
2 |
d |
1 |
|
(1 2 cos cos |
2 |
)d |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
|
2 |
|
|
|
|
|
||
|
1 |
( |
2sin ) |
|
1 |
|
(1 cos 2 )d |
1 |
( |
) |
|
|
3 |
. |
|||||||||||||||||
2 |
0 |
4 |
4 |
2 |
0 |
2 |
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Длина кардиоиды равна
3 |
|
|
2 |
||
|
(кв. ед.)
4. Вычислить площадь фигуры, ограниченной одной аркой циклоиды x=a(t-sint), y=a(1-cost); (0 t 2 ) и осью ОХ.
Решение:
Сделаем чертеж:














 х Площадь фигуры найдем по формуле:
х Площадь фигуры найдем по формуле:
|
t |
|
|
2 |
|
S |
|
y(t) x'(t)dt. |
|
или
|
|
t |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
2 |
|
|
||
S |
|
a(1 cos t) a(1 cos t)dt a |
2 |
|
(1 2 cos t cos |
2 |
t)dt |
|
|
||||||
|
|
|
|
||||
|
0 |
|
|
0 |
|
|
|
|
|
2 |
|
1 cos 2t |
|
|
|
|
|
|
|
2 |
|
|
|
|
a |
2 |
|
(1 |
2 cos t |
)dt a |
2 |
( |
3 |
t 2sin t |
cos 2t |
) |
3 a |
2 |
. |
||
|
|
|
|
|||||||||||||
|
2 |
|
2 |
4 |
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: S=3 а2 (кв. ед.)
Задания для самосоятельного решения:
1. Найдите площадь фигуры, ограниченной линиями. y=x2-3x+2 и y=-2x+8.
2. Вычислить площадь фигуры, ограниченной четырехлепестковой розой
r
2 sin
4 .
.
Длина дуги плоской кривой, объем тела вращения
1.Вычисление длины дуги плоской кривой.
2.Вычисление объема тела вращения.
Теоретическая часть:
Вычисление длины дуги плоской кривой
Для длины дуги незамкнутой плоской кривой без кратных точек (точек самопересечения) используют выражения:
b |
|
dx - в декартовой системе координат; f(x) – |
l |
1 f (x) 2 |
|
a |
|
|
непрерывно дифференцируема на [a,b].
|
2 2 d |
|
l |
- в полярной системе координат; имеет |
непрерывную производную , .
