Для студентов / Лекции / (2)ВЕД / (7)Властивості рівнянь Максвела

7. Властивості рівнянь Максвела

Цей розділ присвячується подальшому аналізу основних властивостей диференціальних рівнянь Максвела. Ми коротко розглянемо їх відповідність

основним принципам електродинаміки, а також встановимо їх узгодженість із законом збереження заряду. Звернемо увагу на суттєво різний характер поведінки потенціальних та вихрових складових електричного і магнітного полів.

а) Узгодженість з основними принципами електродинаміки

Рівняння Максвела

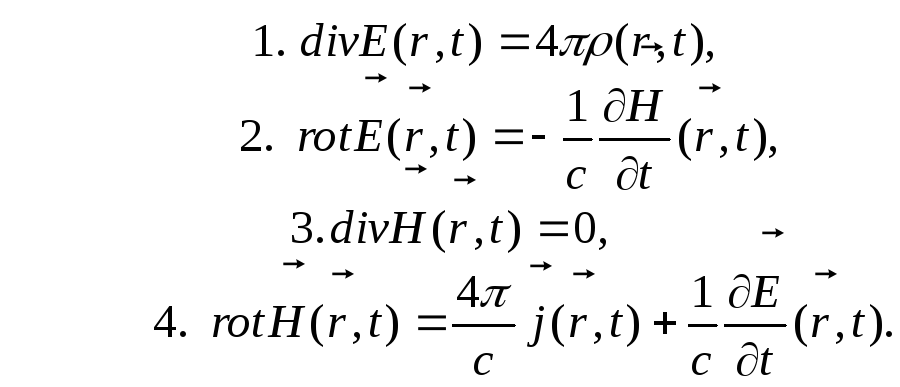(7.1)

є лінійними диференціальними рівняннями з частковими похідними відносно напруженостей електричного і магнітного полів. Лінійність рівнянь гарантує виконання принципу суперпозиції, одного з основних принципів електродинаміки. Так само, залежність напруженостей полів і їх скалярних і векторних джерел від одних і тих же просторових координат і часу свідчить про те, що рівняння Максвела узгоджуються також і з принципом локальності. Вони не допускають подальших узагальнень типу:

,

де є малим у порівнянні з характерними часами змін всіх інших величин, які входять до рівнянь Максвела. З точністю до малих внесків порядку густину заряду можна представити у вигляді: , який явно суперечить принципу локальності.

Узгодженню рівнянь Максвела з принципом відносності буде присвячена окрема глава, в якій буде розвинута спеціальна теорія відносності.

Дещо докладніше зупинимось на їх узгодженості з принципом інваріант- ності рівнянь електродинаміки відносно перетворень просторової і часової інверсії. У згоді з розділом 2, напруженості електричного і магнітного полів, а також дивергенції і ротори від них перетворюються за законами

, , (7.2)

. (7.3)

Густини зарядів і токів мають такі ж самі трансформаційні властивості як заряд і швидкість його руху, тобто

, . (7.4)

Оскільки операції просторової інверсії і диференціювання за часом є незалежними і, як наслідок, комутативними: . Звідси і з (7.2) випливає, що

, . (7.5)

Користуючись законами перетворень (7.2)-(7.5), неважко впевнитись, що ліві і праві частини кожного з рівнянь Максвела перетворюються однаковим чином. Зокрема,

і

.

Це дає підстави стверджувати, що рівняння Максвела є інваріантними відносно операції просторової інверсіх.

Аналогічні співвідношення для оператора часової інверсії мають вигляд (див. означення в розділі 2):

, (7.6)

, , (7.7)

, (7.8)

. (7.9)

На прикладі четвертого рівняння Максвела продемонструємо його інваріантність відносно операції інверсії часу:

.

Так само перевіряється інваріантність відносно - операції і всіх інших рівнянь Максвела.

Дуже важливу роль в сучасній фізиці відіграє операція зарядового спряження, якій відповідає оператор . Він змінює знаки зарядів частинок на протилежні:

. (7.10)

Як наслідок,

, (7.11)

і

. (7.12)

Оператор зарядового спряження комутує з усіма диференціальними операторами, які входять до рівнянь Максвела: , і

. Інваріантність рівнянь Максвела відносно операції зарядового спряження перевіряється безпосередньо.

Слід зазначити, що всі пари операторів комутують між собою. Рівняння електромагнітного поля залишаються незмінними при застосуванні кожного з них. Але в фізиці елементарних частинок зустрічаються і такі взаємодії, які залишаються інваріантними тільки по відношенню до парних операторів типу і навіть трійки операторів .

б) Закон збереження заряду

Важливою властивістю рівнянь Максвела є їх узгодженість із законом збереження заряду. Дійсно, застосуємо оператор до обох частин рівняння 4. Оскільки і , то ми приходимо до рівняння:

.

Підставляючи в нього значення з першого рівняння Максвела, отримуємо:

. (7.13)

Це і є диференціальна форма закону збереження заряду. В цьому легко переконатись, якщо перейти до відповідного інтегрального рівняння. Інтегруючи (7.13) по об’єму і використовуючи теорему Гауса-Остроградського, знаходимо:

. (7.14)

Ми бачимо, що сумарний заряд в об’ємі зменшується тільки за рахунок відтоку заряду через поверхню (на що вказує знак мінус), або зростає тільки за рахунок притоку заряду (в цьому випадку напрямок вектору стає протилежним попередньому). В самому об’ємі джерела або стоки зарядів є відсутніми.

Зазначимо, що закон збереження заряду разом з законами збереження енергії, імпульсу і моменту імпульсу належить до числа фундаментальних законів збереження заряду. Він не пов'язаний з конкретною системою рівнянь електродинаміки, але узгодження рівнянь Максвела з ним є важливим свідченням на користь їх коректності.

в) Рівняння для потенціальних і вихрових електромагнітних полів

У розділі 1, формула було показано, що довільне векторне поле має структуру:

, (7.15)

де гармонійна складова і є потенційними полями, а складова має вихровий характер. Оскільки у всіх точках простору , ми робимо висновок, що магнітне поле є чисто вихровим. Що стосується електричного поля, то його вектор напруженості є сумою як вихрової, так і потенціальної складових:

. (7.16)

Таку ж саму структуру має і тік зарядів:

. (7.17)

Коротко зупинимось на можливих реалізаціях потенціальних і вихрових складових токів. Прикладом потенціального току можуть служити емісійні токи в електронній лампі або електронній пушці. В той же час, тік, який виникає в металічному кільці після його розкручення в площині кільця і різкої зупинки, має характер вихрового току. Тут тік електронів виникає внаслідок сил інерції.

Як бачимо, рівняння Максвела є комбінацією потенціальних і вихрових векторних полів. Вони є незалежними, внаслідок чого рівняння Максвела можна розщепити на сукупності відповідних рівнянь.

Підставляючи (7.16) і (7.17) в рівняння Максвела (7.1)і враховуючи, що

,

для потенціальних і вихрових складових напруженостей поля і знаходимо:

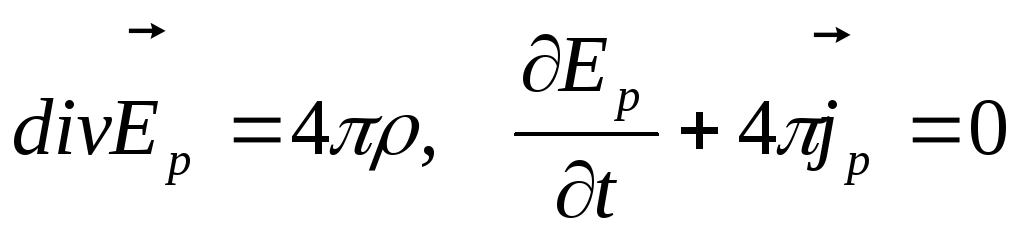, (7.18)

і

. (7.19)

Друге з рівнянь (7.18) не є незалежним. Дійсно, застосуємо до нього операцію :

.

З першого з рівнянь (7.18) випливає, що . З другого боку, згідно закону збереження заряду (7.13): , тобто друге з рівнянь (7.18) виявляється наслідком першого рівняння і закону збереження заряду. Таким чином, замість двох рівнянь (7.18) можна залишите лише одне з них:

, (7.20)

яке співпадає з відповідним рівнянням (5.5) в електростатиці. Рішення цих рівнянь також мають однакову структуру. Зазначимо, що потенціальну складову електричного поля можна представити у вигляді градієнту потенціалу (див. розділ 1): , який задовольняє рівнянню Пуассона:

. (7.21)

Рівняння (7.19) і (7.20) є суттєво різними, завдяки чому просторово-часова еволюція поля буде значно відрізнятись від еволюції полів і . Дійсно, спираючись на (7.19), побудуємо рівняння для напруженості електричного поля. Для цього застосуємо оператор до лівої і правої частин першого з рівнянь (7.19):

.

Для вихрового поля . Замість підставимо його значення з другого рівняння (7.19). У такий спосіб знаходимо, що напруженість електричного поля задовольняє неоднорідному хвильовому рівнянню:

. (7.22)

Таким самим шляхом можна знайти рівняння і для напруженості магнітного поля:

. (7.23)

За межами області скупчення зарядів і токів, рівняння для вихрової складової напруженості електричного поля і напруженості магнітного поля мають особливо простий вигляд:

(7.24)

Це є однорідні хвильові рівняння.

г) Кількість незалежних компонентів електричного і магнітного полів

Напруженості електричного і магнітного полів разом складаються з шести компонентів:

,

які задовольняють 8-ми рівнянням (двом скалярним рівнянням Максвела 1 і 3, і шести скалярним рівнянням, які утворюються з двох векторних рівнянь Максвела 2 і 4). Виходить, що число рівнянь є більшим від числа компонентів. Дуже часто це є свідченням суперечності системи рівнянь. Але у випадку рівнянь Максвела таке утруднення не виникає. В попередньому розділі було встановлено, що рівняння Максвела розщеплюються на несуперечливі системи рівнянь для потенціальних і вихрових складових напруженостей електричного і магнітного полів. Фактично, це означає, що не всі компоненти напруженостей полів є незалежними.

Дійсно, з трьох компонентів потенціальної складовою напруженості електричного поля незалежною є тільки одна. Це обумовлено тим, що є градієнтом від однієї скалярної функції – потенціалу . Так само, скалярне рівняння Максвела 3 () дозволяє одну компоненту напруженості магнітного поля виразити, через дві другі компоненти. Ще два обмеження на компоненти напруженості електричного і магнітного полів накладають рівняння (7.19) або (7.22) і (7.23). Таким чином, число незалежних компонентів напруженостей полів дорівнює трьом. Це обов’язково одна з компонентів електричного поля, яка описує його потенціальну складову, і дві будь які компоненти вихрових складових електричного і магнітного полів.

З цих міркувань випливає, що рівняння Максвела є взаємозалежними і їх використання не є оптимальним шляхом для визначення напруженостей електромагнітного поля.. В подальшому ми будемо, як правило, користуватись електромагнітними потенціалами, які з математичної точку зору є набагато більш зручними. Але в принциповому плані, обраний Максвелом шлях побудови рівнянь електромагнітного поля є найбільш прозорим і чітким.

Зазначимо, що для визначення електромагнітного поля можна використовувати як диференціальні, так і інтегральні рівняння Максвела. Ступінь їх повноти є однаковим. Але використання диференціальних рівнянь є більш доцільним, оскільки вони зразу описують локальні особливості електромагнітного поля та деталі його просторово-часової еволюції.

8. Граничні умови

В типових ситуаціях область , в якій розшукується електромагнітне поле, обмежується поверхнями різних фізичних тіл. Крім того, окремі тіла можуть знаходитись і в самій області . Ми розрізняємо поверхні, які розділяють підобласті з різними фізичними властивостями, а також підобласті з однаковими фізичними властивостями. Поверхні першого типу утворюються, наприклад, коли в необмежений простір вноситься металева куля, а другого типу – при внесені металічної сфери. Зрозуміло, що при пересіченні поверхні того чи іншого типу відбувається суттєва зміна електромагнітного поля. Дійсно, внесемо в постійне електричне поле, яке розповсюджене в необмеженому просторі, металічну кулю. Як добре відомо, електричне поле витискується зсередини кулі. Дійсно, якби цього не відбувалось, всередині кулі встановлювався б постійний тік і приводив кулю до необмеженого нагрівання, що суперечить експериментальним даним. Таким чином, при пересіченні поверхні кулі відбувається швидке зменшення зовнішнього електричного поля до нуля.

Використання рівнянь Максвела для опису електромагнітного поля в поверхневих шарах є складною задачею, оскільки в тонких поверхневих шарах напруженості поля змінюються на скінчену величину. З цього випливає, що модулі і можуть приймати великі значення, а в граничних випадках прямувати до нескінченості. Інакше кажучи, на певній множині точок порушується застосування диференціальних рівнянь і утворюються значні труднощі при побудові розв’язків рівнянь Максвела.

Для подолання цих труднощів, поверхневі шари скінченої товщини замінюються поверхнями нульової товщини. Вважається, що така поверхня розділяє область на підобласті, в яких і є неперервними функціями і побудова розв’язків рівнянь Максвела не викликає утруднень. Знайдені розв’язки зшиваються на поверхні розділу під- областей за допомогою граничних умов.

Перехід до поверхонь нульової товщини супроводжується появою поверхневих зарядів з густиною і поверхневих токів з густиною . Розглянемо більш детально їх означення. Нехай об’ємна густина заряду при

Рис.7.1. Схематична поведінка густини об’ємного заряду в

поверхневому шарі.

пересіченні поверхневого шару в перпендикулярному до нього напрямку змінюється так, як показано на Рис.7.1. При переході до нескінчено тонкої

.

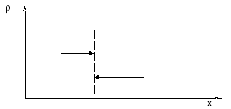
Рис.7.2. Схематична поведінка густини об’ємного заряду в

околі поверхні розділу.

поверхні розділу ми приймаємо, що в області існування поверхневого шару об’ємна густина заряду будується шляхом екстраполяції її значень в шарі, який безпосередньо прилягає до поверхневого шару (Рис.7.2). Зрозуміло, що в загальному випадку на поверхні розділу двох підобластей об’ємна густина заряду змінюється стрибком. Така ж процедура застосовується і до густини об’ємного току зарядів, а також до напруженостей електричного і магнітного полів.

За означенням, густиною поверхневого заряду будемо називати заряд

поверхневого шару, який припадає на одиницю площі поверхні розділу:

. (7.1)

Густина поверхневого току визначається аналогічно:

. (7.2)

В термінах нескінчено тонкої поверхні розділу, є тік, що протікає через одиничний відрізок, орієнтований перпендикулярно лініям поверхневого току.

Всі поверхні розділу вважаються орієнтованими. Як і раніше, орієнтація поверхні , що обмежує об’єм , вибирається у згоді з напрямком руху точки зсередини області зовні. Орієнтація внутрішніх поверхонь, в принципі, може бути довільною, але бажано, щоб вона була максимально узгодженою з орієнтацією поверхні . Підобласть, на яку вказує одиничний вектор нормалі до поверхні розділу, будемо нумерувати індексом «». Під- область з протилежного боку поверхні розділу будемо нумерувати індексом «». В околі довільної точки на поверхні розділу вектори напруженості електричного і магнітного поля природно розкладаються на нормальні і тангенціальні (дотичні) складові: () і () та () і (). Треба зразу ж зазначити, що в кожній підобласті є тільки одна нормальна складова вектора, але нескінчена множина тангенціальних складових. Серед них незалежними є дві, які можна асоціювати з напрямками осей і на дотичній поверхні. Для знаходження умов зшивки нормальних і тангенціальних складових векторів напруженості електричного і магнітного полів звернемось до інтегральних рівнянь електродинаміки. Вони не включають похідних від просторових координат, завдяки чому потоки і циркуляції електричного і магнітного полів в них будуть коректно визначеними.

а) Граничні умови для нормальних складових напруженостей

електричного і магнітного полів

Для знаходження умов зшивки і скористаємось законом Гауса-Остроградського (6.20), в якому об’єм перерізається поверхнею розділу. Нехай позначає площину тієї частини поверхні розділу, яка потрапляє всередину області . Врахуємо, що при переході до нескінчено тонкої поверхні формула (6.20) узагальнюється наступним чином:

. (7.3)

Для спрощення розрахунків оберемо область у формі прямокутної призми, ребра якої є перпендикулярними до поверхні розділу, а основи є симетрично розташованими і паралельними поверхні розділу (Рис.7.3). Будемо вважати, що довжина ребер та ширина і довжина сторін основ є набагато меншими від радіусів кривизни поверхні розділу і характерних масштабів, на яких змінюються електричні поля в підобластях і , а також густина поверхневих зарядів. При виконанні цих умов, від інтегралів (7.3) можна перейти до інтегральної суми:

. (7.4)

Тут позначає потік електричного поля через бокову поверхню призми, а і є середні значення густин зарядів в одній і другій половинах призми. Оскільки напруженості електричного поля в підобластях і є скінченими (інакше застосування диференціальних чи інтегральних рівнянь буде неможливим), то внесок є пропорційним довжині ребра . Спрямуємо тепер до нуля (), тобто наблизимо основи призми до поверхні розділу. Завдяки такому граничному переходу, внески в (7.4), які є пропорційними , зануляються і формула (7.4) переходить в наступну граничну умову для нормальних складових вектора напруженості електричного поля: :

або . (7.5)

Це значить, що на зарядженій поверхні розділу нормальні складові вектору напруженості електричного поля терплять розрив, величина якого є пропорційною поверхневій густині заряду . Граничну умову (7.5) можна записати також у векторній формі:

. (7.6)

Умови зшивки для нормальних складових напруженості магнітного поля і будуються аналогічним чином. З інтегрального закону Гауса (див. (6.20))

зразу ж випливає, що

, (7.7)

тобто нормальні складові напруженості магнітного поля є неперервними на будь якій поверхні розділу. Векторним аналогом (7.6) є гранична умова:

. (7.8)

б) Граничні умови для тангенціальних складових напруженостей