Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Эл.-дин.минимум

.pdf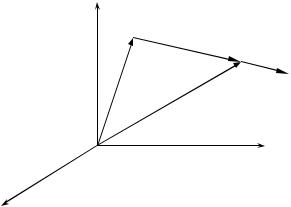

Скачиваний:

Добавлен:

20.05.2015

Размер:

173.26 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Минимум по разделу «Вакуумная электродинамика» для студентов 3го курса физического факультета

ТЕОРИЯ

1. Закон Кулона

Закон Кулона устанавливает значение сил,

действующих со стороны заряда q1

на

заряд q2 и наоборот.

Согласно закону Кулона, сила,

действующая на заряд q2

со стороны заряда

q1 ,

определяется выражением:

q1q2

(1.1)

где R12 = r2 − r1 , R12 =| R12 | , а r1 и r2 – радиус-векторы,

задающие положение зарядов

q1 и q2 . Сила, действующая со стороны заряда q2

на

заряд q1 , определяется

аналогичным образом:

q1q2

= −

q1q2

(1.2)

Здесь R21 = r1 − r2 = −R12 , а R12 = R21 .

Сила – векторная величина. Нужно указывать ее направление и точку приложения.

q1 R12 = r2 − r1

q2 F12

Зная	размерность	[F ] силы взаимодействия двух зарядов (из	закона Ньютона
F = ma	следует, что	[F ] = MLT −2 ), легко записать размерность [q]	электрического
заряда q :


[q] = [R	F	] = L × MLT −2 = M 1 2 L3 2T −1 .			(1.3)

2. Определение напряженности электрического поля

Напряженность E электрического поля – это сила, действующая на единичный положительный заряд со стороны электрического поля:

				E =	F	.		(2.1)

					q
Размерность [E] напряженности электрического поля E :
	[F ]		MLT −2
[E] =		=					= M 1 2 L−1 2T −1 .	(2.2)
	[q]		M	1 2 3 2 −1
				L T

3. Определение напряженности магнитного поля

Напряженность			H магнитного поля –	вектор, определяющий	силу dF ,
действующую на элемент тока d I со стороны магнитного поля, по закону
			dF = [d I, H] .		(3.1)
Здесь d I =	I	d l , I –	величина линейного тока,	c – скорость света, d l –	векторный

	c

элемент длины тока, равный d l = dl × τ , где τ – вектор, задающий Выражение [d I, H] означает векторное произведение векторов d I и

Размерность [H ] напряженности магнитного поля:

[H ] = [F ] ×[c] = M 12 L−12T −1 . [I ] ×[dl]

направление тока.

H .

(3.2)

Размерности напряженностей электрического (2.2) и магнитного (3.2) полей совпадают:

[E] = [H ] .

4. Закон Ампера

Закон Ампера устанавливает значение сил, действующих со стороны элемента тока

d I1 на элемент тока d I2 , и наоборот.
Сила dF12 , действующая со стороны элемента тока d I1 на элемент тока d I2								равна
dF =	1	[d I	,[R		, d I		]] ,	(4.1)
dF =	R3	[d I	,[R		, d I		]] ,	(4.1)
12	R3	1		12		2
	12

Сила, действующая со стороны элемента тока d I2						на d I1 , равна
dF	=	1	[d I		,[R		, d I	]] ,	(4.2)
		R3
21				2		21	1
	12

Из (4.1) и (4.2) следует, что dF21 ¹ -dF12 (убедиться самостоятельно).

5. Плотности заряда и тока

5.1. Объемная плотность заряда ρ – заряд, приходящийся на единицу объема:


			q
				,			дляоднородногораспределениязаряда;

ρ =		V
lim		Dq			=	dq	, длянеоднородногораспределениязаряда.

	V →0	DV				dV
Здесь dq – заряд,		находящийся в элементе объема dV . Размерность объемной
плотности равна [ρ ] = [q]L−3						= M 1 2 L−3 2T −1 .

· Плотность распределения совокупности N точечных зарядов:

ρ(r) = ∑qiδ (r - ri )

i=1

·Связь полного заряда Q с плотностью:

Q = ∫ dq = ∫ ρ dV .

5.2.Поверхностная плотность заряда σ – заряд, приходящийся на единицу площади:

		σ	=		q	,				дляоднородногораспределениязаряда;

σ					S
σ	=				S			dq
				Dq				dq
	σ = lim						=		,	длянеоднородногораспределениязаряда.
	σ = lim						=		,	длянеоднородногораспределениязаряда.
		S →0 DS						dS
Здесь dq –	заряд,		находящийся на элементе поверхности dS . Размерность

поверхностной плотности равна [σ ] = [q]L−2 = M 12 L−1 2T −1 .

5.3. Линейная плотность заряда χ – заряд, приходящийся на единицу длины нити:

	σ =		q
				,			дляоднородногораспределениязаряда;

χ =			l			dq
	Dq
σ	= lim	Dl			=		длянеоднородногораспределениязаряда.

	S →0					dl
Здесь dq – заряд,	приходящийся на элемент длины нити dl . Размерность линейной

плотности равна [χ ] = [q]L−1 = M 1 2 L1 2T −1 .

5.4. Объемная плотность тока j(r) – вектор, равный по модулю току,

проходящему через единичную площадку, перпендикулярную линиям тока, и

направленный по касательной к линии тока в данной точке: j(r) = j × τ(r) ,

где τ(r) – единичный вектор, направленный по касательной к линии тока в данной точке.

Объемная плотность тока может быть записана в виде j(r) = ρ (r) × v(r) ,

где v(r) = v × τ(r) – вектор скорости движения зарядов.

5.5. Поверхностная плотность тока i(x, y) определяется как вектор, равный по модулю току, проходящему через единичный отрезок, перпендикулярный линиям тока,

и направленный по касательной к линии тока в данной точке:

i(x, y) = i × τ(x, y) .

Аналогично (3.4') можно написать

i(x, y) = σ (x, y) × v(x, y) .

6. Закон сохранения заряда в дифференциальной форме

∂ρ + div j = 0 .	(6.1)
∂t

7. Силовые линии и эквипотенциальные поверхности

Силовая линия векторного поля A – линия, в каждой точке которой вектор A

направлен по касательной к ней. Уравнение силовых линий в произвольной ортогональной системе координат имеет вид:

h1dq1	=	h2dq2	=	h3dq3	(7.1)
A1		A2		A3

где h1 , h2 , h3 – коэффициенты Ламе.

Силовые линии всегда перпендикулярны к эквипотенциальным поверхностям.

Силовые линии не пересекаются, т.к. в противном случае поле A было бы неоднозначно заданным.

8. Градиент, дивергенция, ротор. Оператор набла

8.1. Градиент скалярного поля ϕ – вектор,

задающий направление наибольшего

роста

функции ϕ и численно равный

скорости

роста в этом направлении.

произвольной ортогональной системе координат

gradϕ задается выражением:

grad ϕ =

∂ϕ

(8.1)

h1 ∂q1

h2 ∂q2

h3 ∂q3

8.2. Дивергенция векторного поля A в точке r – плотность потока векторного поля

A через произвольную замкнутую поверхность S , охватывающую точку r :

div A = lim

∫ AdS

(8.2)

S →0

V →0

Здесь

V – объем, охватываемый поверхностью S .

∙Физический смысл: плотность скалярных источников векторного поля A .

∙Геометрический смысл: мера расходимости силовых линий поля A .

Впроизвольной ортогональной системе координат:

div A =

∂(h h A )

2 3 1

3 2

1 2

(8.3)

h h h

∂q

1 2 3

8.3. Ротор векторного поля

в точке

–

это вектор,

проекция которого на

направление n определяется поверхностной плотностью циркуляции векторного поля

A :

(rot A)n = lim

∫ Ad l

(8.4)

L→0

S →0

где Ln – замкнутый контур, лежащий в плоскости, перпендикулярной вектору n , Sn

–

площадь участка поверхности, ограниченной контуром Ln .

∙ Физический смысл: rot A –

плотность векторных источников поля A .

∙Геометрический смысл: rot A – мера завихренности силовых линий поля A .

Впроизвольной ортогональной системе координат

	1	h1e1		h2e2		h3e3
rot A =		∂ ∂q1		∂ ∂q2		∂ ∂q3		.	(8.5)

	h1h2h3
		h A		h A		h A
		1	1	2	2	3	3

8.4. Оператор набла в произвольной ортогональной системе координат имеет вид:

Ñ = e1

+ e2

+ e3

¶ .

¶q

· Свойства:

а) Ñ – оператор дифференцирования:

R R R

Ñ(u × v) = Ñu (u × v) + Ñv (u × v) ;

b) Ñ – вектор.

Основные операции:

a) gradϕ = Ñϕ ;

b) div A = (Ñ × A) ;

c) rot A = [Ñ ´ A] .

Вид оператора набла в

· ДСК:

Ñ = i

+ j

+ k

¶x

¶z

¶y

ЦСК:

eα

Ñ = e

+ e

ρ ¶ρ

ρ ¶α

¶z

· ССК:

eϑ

eα

Ñ = er

¶ϑ

r sin ϑ ¶α

¶r

(8.6)

(8.7)

(8.8)

(8.9)

9. Законы электромагнетизма

9.1. Теорема Гаусса-Остроградского о свойствах электрического поля

Поток	вектора напряженности E электрического поля через	произвольную
замкнутую	поверхность S пропорционален величина заряда	QS = ∫ ρ (r)dV ,
		V

находящегося в объеме V , ограниченном этой поверхностью:

∫ E × d S = 4π QS .

Здесь d S = n dS , n – вектор нормали к поверхности. Коэффициент 4π соответствует системе СГС.

9.2. Закон Фарадея об электродвижущей силе

Работа по перемещению единичного точечного положительного заряда вдоль

замкнутого контура называется электродвижущей силой: э.д.с. = ∫ E × d l . Контурный

интеграл ∫E ×d l – циркуляция вектора напряженности электрического поля. В

электростатике∫E × d l = 0 (условие потенциальности электрического поля).

Циркуляция вектора напряженности E изменяющегося электрического поля вдоль

замкнутого контура L пропорциональна скорости изменения магнитного потока ΦH

через произвольную поверхность SL , натянутую на этот контур:

∫ E × d l = -	1	dFH	,

L	c dt

где

FH = ∫ H × d S .

9.3.Закон Гаусса об отсутствии магнитных зарядов

Поток вектора напряженности H магнитного поля через произвольную

замкнутую поверхность равен нулю:

∫ H × d S = 0 .

9.4.1.Закон Био-Савара-Лапласа для статического магнитного поля

(циркуляционная теорема)

Циркуляция вектора напряженности H магнитного поля вдоль замкнутого контура L пропорциональна току, протекающему через произвольную поверхность SL ,

натянутую на этот контур:

	4π				NS L
					∑ I k ,	длялинейныхтоков;
			c		∑ I k ,	длялинейныхтоков;
			c
∫H × d l =		4π			k =1	дляраспределенныхтоков.
L				∫ j× d S,		дляраспределенныхтоков.
			c	SL
				SL

Здесь NSL – число линейных проводников, проходящих через поверхность S L .

9.4.2. Закон Био-Савара-Лапласа-Максвелла для изменяющегося магнитного

поля

Циркуляция вектора напряженности H изменяющегося магнитного поля вдоль замкнутого контура L пропорциональна сумме токов зарядов и «токов смещения»,

протекающих через произвольную поверхность, натянутую на этот контур:

∫H × d l =	4π	∫ j× d S (для распределенных токов),
∫H × d l =	c	∫ j× d S (для распределенных токов),
L	c	SL
L		SL
где
		j = jзар	+	1	¶E ,
		j = jзар	+		¶E ,
				4π ¶t

E– вектор напряженности электрического поля.

10.Уравнения Максвелла электромагнитного поля в вакууме

div E = 4πρ,

rot E = -		1		¶H ,
		c
				¶t
div H = 0,			(10.1)

rot H =	4π			j +	1	¶E .

	c				c ¶t

Уравнения Максвелла, фактически, представляют собой задание явного вида скалярных ( div E и div H ) и векторных ( rot E и rot H ) источников электрического и магнитного полей.

· Граничные условия (общий вид):

En(1) - En(2)		= 4πσ ,
	E (1)	= E (2) ,
	τ		τ		(10.2)
	H n(1)	= H n(2) ,
H (1)	- H (2)	=	4π	i .

τ	τ		c ν

Здесь σ и i – плотности поверхностных зарядов и токов соответственно, индексы n , τ и ν обозначают нормальные ( n ) и тангенциальные (τ ,ν ) составляющие к

поверхности раздела E и H . Единичные векторы n , τ и ν		связаны между собой
соотношением:
R		(10.3)
ν = [n, τ].		(10.3)
· Граничные условия в ДСК:
Ez(1) - Ez(2) = 4πσ ,
H z(1)	= H z(2) ,
Ex(1)	= Ex(2) ,

H (1)

− H (1)

4π

Ey(1)

= Ey(2) ,

(10.4)

H (1)

− H (1)

= −

4π

∙ Уравнения электростатического поля:

div E = 4πρ , rot E = 0 .

(10.5)

∙ Уравнения магнитостатического поля:

div H = 0 , rot H =

4π

j .

(10.6)

11. Уравнения Пуассона-Лапласа для электро- и магнитостатического полей

11.1. Уравнения электростатического поля

∙ Уравнение Пуассона:

ϕ = −4πρ .

(11.1)

Здесь учтено, что E = − grad ϕ . ∙ Уравнение Лапласа:

ϕ = 0 .

∙ Граничные условия:

ϕ1 = ϕ2 ,

∂ϕ2 − ∂ϕ1 = 4πσ . ∂n ∂n

∙ Граничные условия в ССК:

	ϕ1 (r,ϑ,α ) = ϕ2 (r,ϑ,α ),
∂ϕ2	−	∂ϕ1	= 4πσ .

∂r		∂r
			r =R

11.2. Уравнения магнитостатического поля

∙ Уравнение Пуассона:

A = − 4π j. c

(11.2)

(11.3)

(11.4)

∙ Уравнение Лапласа:

A = 0 .

(11.5)

∙ Граничные условия:

A1 = A2 ,

(rot A

− rot A

)

4π

i .

(11.6)

2 τ

∙ Граничные условия в ССК:

A1 (r,ϑ,α ) = A2 (r,ϑ,α ),

∂A(1)

∂(rA(1) )

∂A(2)

∂(rA( 2) )

4π

− sin ϑ

−

− sin ϑ

i .

r sin ϑ

∂α

∂r

∂(rA(1) )

∂( A(1) )

∂(rA(2) )

∂( A( 2) )

4π

−

= −

i .

∂ϑ

∂r

12.Электромагнитные потенциалы

∙ Определение скалярного ϕ и векторного A потенциалов:

E = − grad ϕ − 1 ∂A , H = rot A . c ∂t

∙ Потенциалы ϕ ′ , A′ и ϕ , A эквивалентны, если они связаны соотношениями:

A′ = A + grad χ , ϕ′ = ϕ − 1 ∂χ . c ∂t

∙ Калибровка Лоренца:


div A +					1	∂ϕ = 0 .

					c ∂t
∙ Уравнения для скалярного ϕ и векторного A потенциалов:
ϕ −		1		∂ 2ϕ			= −4πρ ,

		c2 ∂t 2
A −	1		∂2 A				= −	4π	j .

	c2 ∂t 2							c

1 / 21 2 > Следующая >>>

Соседние файлы в папке (2)ВЕД

#
20.05.2015188.93 Кб9(6)Узагальнення Максвела. Рівняння Максвела.doc
#
20.05.2015573.95 Кб12(7)Властивості рівнянь Максвела.doc
#
20.05.2015180.74 Кб15(9)Електромагнітні потенціали.doc
#
20.05.2015295.42 Кб6Итоговая ДКР по ВЭД.doc
#
20.05.201594.21 Кб10Эквипотенциальные поверхности вблизи особых точек.doc
#
20.05.2015173.26 Кб8Эл.-дин.минимум.pdf