Для студентов / Лекции / (3)СТВ / (4)Електродинаміка в СТВ

4. Електродинаміка в СТВ

Цей розділ присвячується: 1) розгляду представлення електромагнітного поля в чотиривимірному комплексному просторі СТВ; 2) побудові чотиривимірних рівнянь Максвела і встановленню їх інваріантності відносно перетворень Лоренца і 3) побудові чотиривимірної форми законів збереження електромагнітного поля.

а) Чотиривимірна форма диференціального закону збереження заряду

У згоді з () закон збереження заряду в ЛІСВ описується диференціальним рівнянням:

. (4.1)

Для погодження з принципом відносності, таку саму форму закон збереження заряду повинен мати і в якійсь іншій ІСВ:

. (4.2)

Розглянемо тепер вигляд диференціального рівняння (4.1) в чотиривимірному комплексному просторі СТВ. Має місце наступний очевидний ланцюжок перетворень:

.

Вводячи чотирикомпонентну величину , останнє з рівнянь можна переписати у вигляді:

або . (4.3)

Аналогічно переписується і рівняння (4.2):

або . (4.4)

Збереження форми рівняння, або, як кажуть, його коваріантність відносно перетворень Лоренца, можливе лише за умови, що величини , представляють собою сукупність компонентів чотиривектора. Дійсно, комбінація є спорідненою до скалярного добутку двох чотиривекторів . Елементарно встановлюється, що цей добуток є інваріантним відносно перетворень Лоренца:

.

Тут на останньому кроці ми скористались умовою ортогональності () матриць , які задають перетворення Лоренца. З рівнянь (4.3) і (4.4) випливає, що комбінація двох ненульових величин, з яких представляє собою компоненти чотири вектора, зберігає свій вигляд і у довільній ІСВ. Звідси і інваріантності можна зробити висновок, що і складові другої величини, , також утворюють компоненти чотиривектора . Його прийнято називати чотиривектором току: . Закон перетворення його компонентів є стандартним для чотиривекторів:

. (4.5 )

Повертаючись до тривимірних змінних, на основі (4.5) знаходимо:

. (4.6)

б) Чотиривекторний потенціал електромагнітного поля

Найкоротшим шляхом встановити вигляд електромагнітних потенціалів у чотиривимірному комплексному просторі СТВ можна, звернувшись до калібровочної умови Лоренца (в ЛІСВ ):

.

У згоді з принципом відносності, такий самий вигляд вона зберігає і в довільній ІСВ :

.

Порівнюючи калібровочні умови Лоренца в і зі структурою рівнянь (4.1) і (4.2), які відповідають закону збереження заряду, можна зразу ж прийти до висновку, що аналогом (4.3) і (4.4) будуть чотиривимірні рівняння:

: , : , (4.7)

де - компоненти читирипотенціалу і

. (4.8)

Тривимірний аналог закону перетворення (4.8) набуває вигляд:

, , , . (4.9)

в) Тензор електромагнітного поля

Для побудови представлення напруженостей електричного і магнітного полів () у чотиривимірному комплексному просторі, скористаємось 1) співвідношеннями: , , які пов’язують напруженості і потенціали, і 2) тим фактом, що векторний і скалярний потенціали об’єднуються в чотиривектор за правилом: . У згоді з цим,

,

.

Подібну структуру мають і компоненти напруженості магнітного поля:

.

Фактично, це означає, що компоненти напруженостей електричного і магнітного полів у чотиривимірному комплексному просторі є компонентами антисиметричного тензора

, (4.10)

який прийнято називати чотиритензором електромагнітного поля. Згідно написаним вище співвідношенням, компоненти мають вигляд:

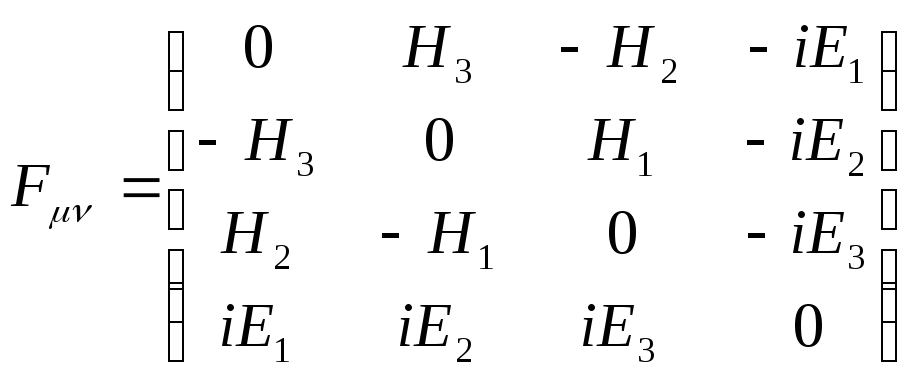. (4.11)

При переході від однієї ІСВ до другої компоненти перетворюються за стандартним законом:

. (4.12)

Скористаємось ним, для встановлення взаємозв’язку між компонентами

() і (). Проілюструємо деталі застосування (4.12) на прикладі компонент і . Враховуючи, що , для отримуємо:

.

Так само,

.

Остаточно, шукані закони перетворення приймають вигляд:

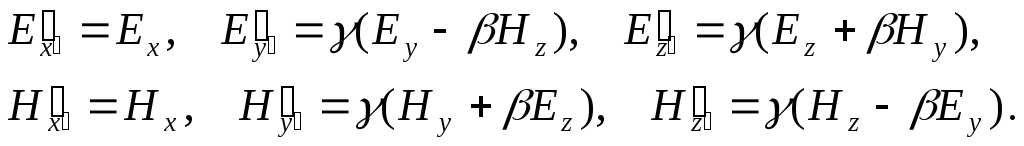(4.13)

Їх також можна представити у векторній формі:

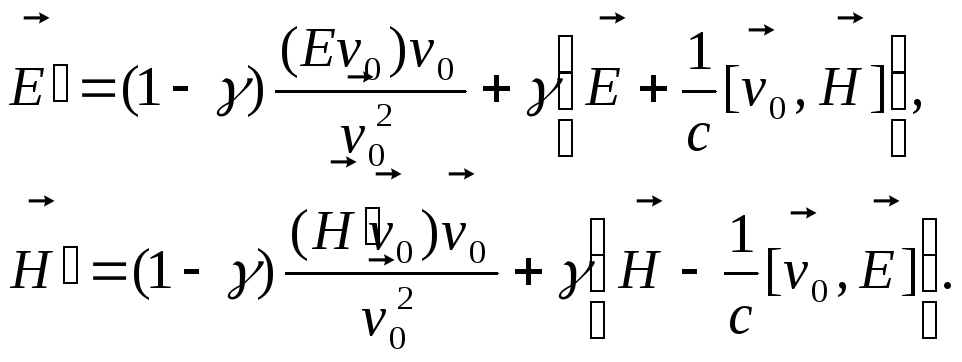(4.14)

В тому випадку, коли напрямок відносної швидкості співпадає з напрямком осей і , формули (4.14) переходять у (4.13).

г) Інваріанти електромагнітного поля

З перетворень (4.12) – (4.14) випливає, що компоненти тензора електромагнітного поля так само як і компоненти () напруженостей електричного і магнітного полів, в загальному випадку не залишаються незмінними: при 1) довільних поворотах в підпросторі () і 2) перетвореннях Лоренца. В обох випадках вони пов’язуються між собою певними лінійними співвідношеннями.

Проте з компонентів і відповідних компонентів () можна утворити комбінації, які будуть залишатись інваріантними відносно обох вказаних вище типів перетворень. Нижче ми розглянемо побудову білінійних інваріантних комбінацій. Найбільш загальним шляхом їх можна побудувати, розглянувши власні значення тензора , які, власне, і будуть шуканими інваріантами. Переконаємось, перед усім, що є симетричним тензором. Дійсно, . Його власні значення знаходяться з рівняння:

.

В розгорнутому вигляді воно має вигляд:

,

де коефіцієнти є функціями компонентів тензора другого, четвертого, шостого і восьмого порядків відповідно. Їх обчислення є вельми громіздким.

Тому ми скористаємось більш простим методом. З компонентів () можна сконструювати три незалежні білінійні комбінації, які є інваріантними відносно довільних поворотах в підпросторі (). Це є квадрати векторів напруженості електричного і магнітного полів і їх скалярний добуток: . Тепер з’ясуємо, чи є вони інваріантними відносно перетворень Лоренца. Відповідь на це запитання стає очевидною при переході до компонентів тензора електромагнітного поля . Неважко впевнитись, що

, (4.15)

, (4.16)

. (4.17)

Із співвідношень (4.15) і (4.16) випливає, що і , кожний сам по собі, не є інваріантними відносно перетворень Лоренца, але цій умові задовольняє їх бінарна комбінація:

. (4.18)

Таким чином, «квадрат» чотиритензора: є, очевидно, одним з шуканих нами інваріантів електромагнітного поля.

Ще один інваріант задається формулою (4.17). Дійсно, розташування індексів підказує нам, що права частина (4.17) є згорткою компонентів тензора електромагнітного поля з повністю антисиметричним тензором четвертого рангу :

. (4.19)

Це стає цілком зрозумілим, якщо згадати означення (див. ()):

(4.20)

і скористатись наступним ланцюжком рівнянь, які випливають з нього:

Додамо, що при перетвореннях Лоренца тензор перетворюється стандартним чином:

і зберігає свої значення згідно (4.20). Дійсно, розглянемо компоненту . Вона дорівнює:

.

Оскільки , , і , то

.

Цілком аналогічно встановлюється ідентичність і всіх інших компонентів.

Використовуючи умови ортогональності (3.8) для матриць , безпосередньо переконуємось, що згортка тензорів в правій частині (4.19) також є інваріантною відносно перетворень Лоренца.

Інваріантність скалярного добутку векторів можна встановити і дещо іншим шляхом. Для цього достотно обчислити детермінант тензора електромагнітного поля. Неважко впевнитись, що вказаний детермінант дорівнює:

, (4.21)

і є інваріантним відносно перетворень Лоренца. Дійсно, значення компонентів тензора електромагнітного поля в різних ІСВ пов’язані між собою стандартним законом:

.

Оскільки детермінант добутку дорівнює добутку детермінантів від множників, то

.

У згоді з (3.13), , так що і .

Інваріантність бінарних комбінацій (4.18) і (4.19), побудованих нами з компонентів векторів напруженості електромагнітного поля, означає, що відповідні комбінації дорівнюють одна одній тільки у точках і , пов’язаних між собою перетвореннями Лоренцо:

(4.22)

г) Рівняння для електромагнітних потенціалів в чотиривимірній формі

Згідно (І.9.6), електромагнітні потенціали задовольняють рівнянням:

Переходячи до компонентів векторного потенціалу, з другого рівняння отримуємо:

Приймаючи до уваги, що і , першому з рівнянь можна надати вигляд:

.

З двох останніх рівнянь, таким чином, випливає, що компоненти чотири-потенціалу електромагнітного поля задовольняють рівнянню:

, (4.23)

де є оператором Даламбера, який в чотиривимірному просторі має вигляд (3.28): .

Комбінація є чотиривектором, оскільки є скалярним диференці-альним оператором. В правій частині (4.23) також знаходиться чотиривектор. Звідси випливає, що при перетвореннях Лоренца ліва і права частини рівняння (4.23) перетворюються однаковим чином, тобто вигляд рівняння в іншій ІСВ буде таким самим, як і у вихідній лабораторній ІСВ. Інакше кажучи, рівняння електродинаміки у представленні електромагнітних потенціалів є інваріантними відносно перетворень Лоренца.

д) Рівняння Максвела в чотиривимірній формі

Побудуємо, насамперед, чотиривимірну форму першого з рівнянь Максвела.

Перепишемо його в компонентах:

.

Замінимо тепер 1) компоненти напруженості електричного поля відповідними компонентами тензора електромагнітного поля (див. (4.11)):

,

і 2) густину заряду його виразом через четверту компоненту чотири- вектора току:

.

В результаті перше з рівнянь Максвела набуває вигляду:

(4.24)

Тут ми переставили місцями індекси у тензора електромагнітного поля і додали внесок , який дорівнює нулю (див. (4.11)).

Подібна структура рівняння є також властивою для четвертого рівняння Максвела. Дійсно, розглянемо перетворення проекції цього рівняння на вісь :

.

Неважко бачити, що останнє рівняння, а також дві інші проекції четвертого рівняння Максвела можуть бути записаними у вигляді:

, (4.25)

Спів ставляючи (4.24) і (4.25), ми бачимо, що перше і четверте рівняння Максвела об’єднуються в наступне чотиривимірне рівняння:

. (4.26)

Покажемо тепер, що друге і третє рівняння Максвела також об’єднуються в одне рівняння, але дещо іншої структури. Це стає зразу зрозумілим після перетворення третього рівняння Максвела. Дійсно,

Введемо за означенням, оператор циклічної перестановки:

.

Тоді перше рівняння набуває вигляду:

. (4.27)

Аналогічно перетворюється і друге рівняння. Так, його проекція на вісь трансформується наступним чином:

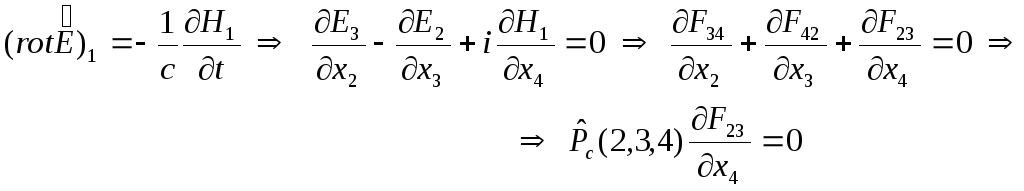. (4.28)

Так само перетворюються друга і третя проекції:

, (4.29)

. (4.30)

Неважко зрозуміти, що всі чотири рівняння (4.24) – (4.27) природним чином об’єднуються в одне рівняння, яке має вигляд:

, . (4.31)

Оскільки тензор електромагнітного поля є антисиметричним, то рівняння (4.31), фактично, є тотожністю. Дійсно, . Циклічна перестановка індексів, як неважко бачити, приводить до нуля тотожно:

.

Фактично, рівняння (4.31) є однією з реалізацій тотожності Якобі.

Рівняння (4.26) та (4.31) і є рівняннями Максвела у чотиривимірному просторі СТВ. В першому з них, з обох боків знаку рівності стоять чотири- вектори і . При перетвореннях Лоренца, які задаються матрицею , вони трансформуються однаковим чином, тобто, їх структура при переході від однієї ІСВ до іншої ІСВ залишається незмінною. Це означає, що рівняння Максвела є коваріантними відносно перетворень Лоренца. Теж саме можна сказати і про виконання тотожності (4.31) в різних ІСВ.

e) Чотиривимірна форма сили Лоренца

В цьому підрозділі буду розглянуто чотиривимірний вигляд сили, яка діє на електричний заряд з боку електромагнітного поля, так званої сили Лоренца:

.

Як і в попередніх розділах, розглянемо вираз однієї з проекцій сили і перейдемо в ньому до чотиривимірних образів тих величин, які входять до нього. Так, на першому кроці проекція сили на вісь трансформується наступним чином:

. (4.32)

Тепер потрібно перейти до компонентів чотиришвидкості. У згоді з означенням (див. (3.18) і (3.19)):

,

ми отримуємо:

,

Після підстановки цих виразів в (4.32), - компонента сили Лоренца набуває вигляду:

. (4.33)

Неважко впевнитись, що так само трансформуються і дві інші компоненти сили, тобто

. (4.34)

Природним шляхом тривимірна сила Лоренца (4.34) узагальнюється наступним чином:

. (4.35)

В подальшому силу, компоненти якої задаються формулою , будемо називати чотиривимірною силою Лоренца. Її компоненти дорівнюють:

, (4.36)

і, як бачимо, четверта компонента чотиривимірної сили Лоренца співпадає з потужністю дії електромагнітних сил. Додамо, що таку ж саму структуру мають і всі інші чотиривимірні сили.

ж) Характер неоднозначності чотиривимірних потенціалів

В розділі (І.9) було показано, що електромагнітні потенціали і є еквівалентними, якщо вони пов’язані співвідношеннями:

.

В цьому випадку вони приводять до одних і тих же значень напруженостей електричного і магнітного полів. При переході до чотиривимірного простору СТВ написанні співвідношення узагальнюються тривіальним чином:

, якщо . (4.37)

Неважко впевнитись, що значення компонентів тензора електромагнітного поля залишаються незмінними: , як це і повинно бути.