Для студентов / Лекции / (3)СТВ / (3) Чотиривимірний простір подій в СТВ

3. Чотиривимірний простір подій в СТВ

В класичній фізиці положення матеріальної точки задається радіусом-вектором і часом . Використання трьох компонент радіус-вектора і окремо часової змінної є цілком природним, оскільки спирається на уявлення про існування абсолютних простору і часу. При переході від однієї ІСВ до другої ІСВ плин часу вважається незмінним, а просторові координати точки змінюються у згоді з простим геометричним правилом побудови суми двох векторів.

Ситуація радикально змінюється при переході до СТВ Айнштайна. Тут положення точки в різних ІСВ задаються власними наборами координат точки і часу: і - в ІСВ , і і - в ІСВ . Зв'язок між ними описується перетвореннями Лоренца, найважливішою рисою яких є залежність плину часу в одній ІСВ від просторових координат точки і часу в другій ІСВ і навпаки. Це вказує на те, що просторові і часову координати точки є доцільним розглядати не окремо, а як незалежні координати точки в підходящому чотиривимірному просторі подій.

а) Побудова чотиривимірного простору подій

Для побудову такого чотиривимірного простору будемо відштовхуватись від найважливішого кінематичного інваріанту відносно перетворень Лоренца – інтервалу руху матеріальної точки:

.

Нові чотиривимірні координати точки будемо вибирати у такий спосіб, щоб інтервал руху точки зводився до відстані між двома відповідними сусідніми точками у чотиривимірному просторі. Здається цілком зрозумілим, що такі координати повинні мати вигляд:

(3.1)

Тоді,

, (3.2)

тільки знаком відрізняється від квадрату диференціала чотиривимірного вектора . В другій ІСВ координати точки задаються чотири- вектором: .

Зв'язок між чотиривимірними координатами точки в різних ІСВ повинен описуватись лінійними співвідношеннями:

, (3.3)

оскільки тільки в цьому випадку прямолінійний і рівномірний рух точки в одній ІСВ залишається таким же і в другій ІСВ. Завдяки лінійності перетворень такий самий закон перетворень є справедливим і для самих координат:

або . (3.4)

У формулі (3.3), а також у всіх подібних, по індексам, що повторюються, відбувається сумування: (). Індекс, по якому відбувається сумування, називають німим індексом. Його можна обирати довільним чином, тобто, має місце рівняння: Існує домовленість, що сумування від до позначається латинськими буквами, а

від до - грецькими.

Для знаходження елементів матриці , яка відповідає лінійному перетворенню (3.3) в 4-вимірному комплексному просторі, перепишемо перетворення Лоренца (1.16) у нових позначеннях:

.

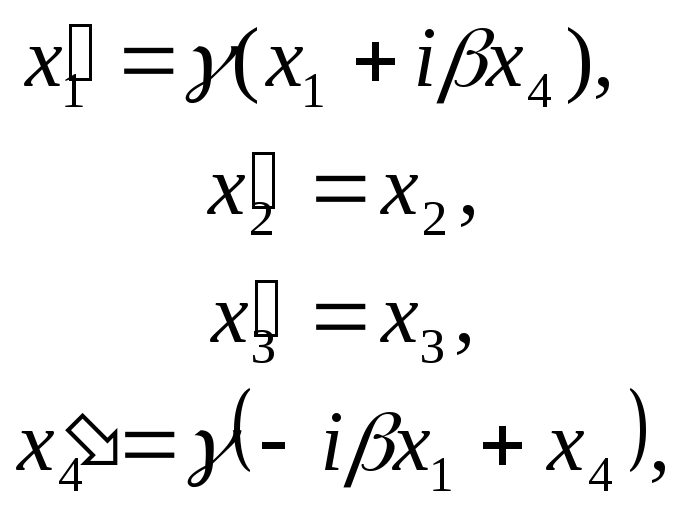Порівнюючи ці співвідношення з (3.4), знаходимо наступні значення елементів матриці :

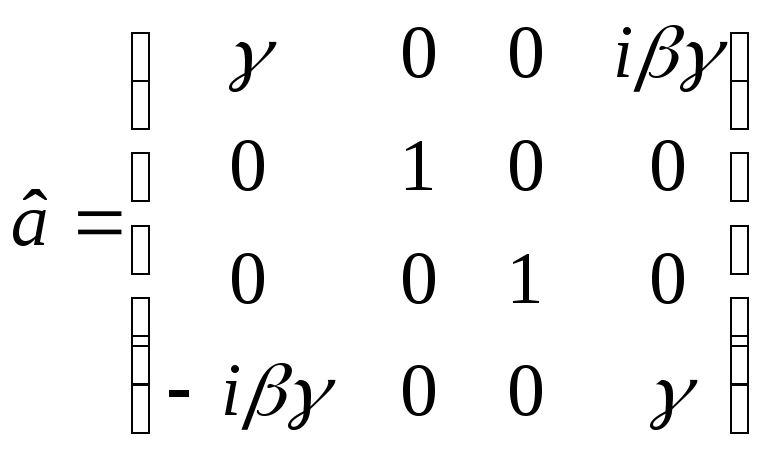. (3.5)

Нагадаємо, що вигляд матриці відповідає стандартному випадку, коли СК двох ІСВ і рухаються одна від одної вздовж осей і , а дві інші пари осей є паралельними між собою.

б) Властивості матриці перетворень

Доведемо одну важливу властивість матриці , відому як властивість ортогональності:

, (3.6)

де - одинична матриця. Дійсно, з інваріантності інтервалу руху і (3.2) випливає:

або . (3.7)

Підставляючи замість диференціалів штрихованих координат в (3.7) вирази і (див. (3.3)), отримуємо:

.

Співвідношення ортогональності (3.6) випливає безпосередньо з рівності крайніх лівого і правого виразів.

Так само можна переконатись в справедливості і другої умови ортогональності:

. (3.8)

Далі, матриця (3.5) відповідає переходу від набору координат в ІСВ до набору координат в ІСВ . Переходу від до відповідає зворотна матриця:

. (3.9)

Оскільки руху ІСВ відносно ІСВ відповідає тільки зміна знаку швидкості, то

, (3.10)

де - матриця, транспонована . Остання властивість випливає безпосередньо з вигляду (3.5).

Оскільки , то

. (3.11)

Враховуючи, що і , з (3.11) отримуємо:

, (3.12)

тобто . В граничному випадку, коли , перетворення Лоренца прямує до тотожного перетворення координат, для якого . Звідси ми робимо висновок, що детермінант матриці перетворень Лоренца дорівнює одиниці:

. (3.13)

Детермінант матриці є безпосередньо пов’язаним з якобіанами прямого і зворотного перетворень. Тому ми робимо висновок:

==. (3.14)

Звідси випливає, що елемент 4-об’єму , який тільки постійним коефіцієнтом () відрізняється від , повинен бути інваріантним відносно перетворень Лоренцо:

або . (3.15)

Дійсно,

.

в) Чотиривимірна швидкість матеріальної точки

Розглянемо означення компонент тривимірної швидкості: . При переході до координат чотиривимірного простору вони отримують вигляд:

. (3.16)

Така похідна не має певної розмірності, оскільки частка від поділення на , які є компонентами чотирьохвимірного радіус-вектору, не є ні скаляром, ні вектором, ні тензором другого рангу. Для побудови вектора чотиривимірної швидкості диференціал часу в знаменнику (3.16) доцільно замінити на диференціал власного часу, помножений на :

. (3.17)

Означений у такий спосіб, диференціал власного часу є інваріантним відносно перетворень Лоренца. Тоді, за означенням, компоненти вектора швидкості точки дорівнює:

. (3.18)

В явному вигляді ці компоненти дорівнюють:

. (3.19)

Компоненти чотиривекторів швидкості в двох різних ІСВ пов’язані між собою перетвореннями:

, (3.20)

цілком подібними до тих (3.10), що пов’язують між собою компоненти чотирьох радіус-вектора. Фактично, формула (3.20) представляє собою закон додавання швидкостей, записаний у чотиривимірній формі. Дійсно, згідно (3.20), компонента швидкості в є пов’язаною з компонентою в

співвідношенням:

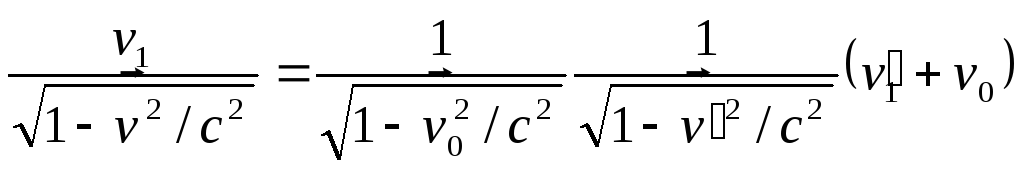. (3.21)

Оскільки квадрати модулів швидкості включають і всі інші її компоненти (,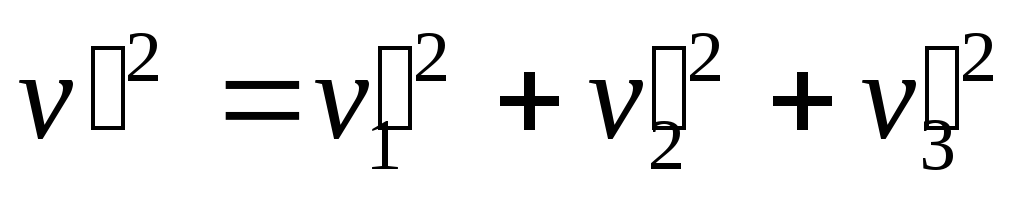), то рівняння (3.21) потрібно було б доповнити законами перетворень всіх інших компонент. Виключно для спрощення, обмежимось випадком, коли швидкості точки направлені вздовж , тобто вздовж осей і . Формула (3.21) переходить в більш просту:

.

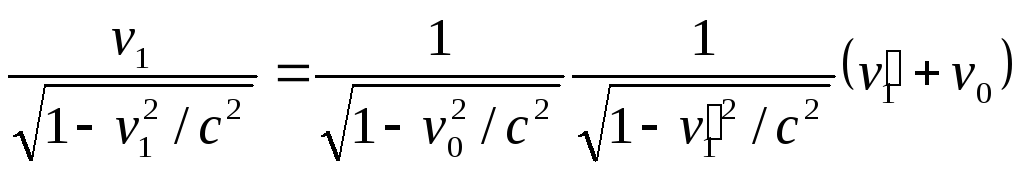Її можна переписати у вигляді:

,

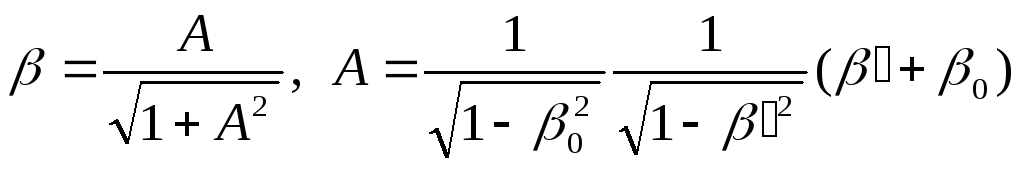де смисл позначень є зрозумілим. Після простих алгебраїчних перетворень остаточно знаходимо:

або .

Отриманий результат повністю співпадає з (2.).

Квадрат чотиришвидкості точки задовольняє співвідношенню:

, (3.22)

яке безпосередньо випливає з означення (3.18) (=). Це значить, що одна з компонент швидкості є залежною від трьох інших. З (3.22), а також з означення (3.18) знаходимо, що квадрат чотиришвидкості є інваріантним відносно перетворень Лоренца:

. (3.23)

г) Чотиривимірне прискорення матеріальної точки

За означенням, чотиривектор прискорення точки визначається формулою:

або . (3.23)

У згоді з (3.19) компоненти є пов’язаними з тривимірними компонентами прискорення співвідношеннями:

(3.24)

Диференціюючи за інтервалом обидві частини співвідношення (3.22), знаходимо:

, (3.25)

тобто, чотири вектори швидкості і прискорення виявляються ортогональними.

Закони перетворення компонентів чотириприскорення, очевидно, мають вигляд:

або . (3.26)

Оскільки компоненти чотириприскорення і тривимірного вектора прискорення точки пов’язані між собою співвідношеннями (3.24), можна впевнитись, що формули (3.26) є економною формою запису законів додавання прискорень (2.19) і (2.20).

д) Закони перетворення похідних у чотиривимірному просторі

Нехай, за означенням, чотиривимірний оператор набла дорівнює:

. (3.27)

За його допомогою оператор Даламбера переписується у вигляді:

. (3.28)

Розглянемо тепер закони перетворення компонентів цих диференціальних операторів при перетвореннях Лоренца. Оскільки , то значення похідних в різних ІСВ повинні бути пов’язаними між собою співвідношеннями:

.

Далі, оскільки , то

,

і закон перетворення похідних набуває вигляду:

. (3.29)

Таким чином, ми робимо висновок, що компоненти чотиривимірного оператора набла, перетворюються подібно до компонентів стандартного чотиривектора. Оскільки квадрат чотиривектора є інваріантним відносно перетворень Лоренца, то у згоді з (3.28) можна стверджувати, що оператор Даламбера також є інваріантним відносно них:

. (3.30)

Інакше кажучи, оператор Даламбера є скалярним диференціальним оператором другого порядку.