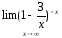Тест 1
Тест по математическому анализу.
( для студентов экономического факультета, обучающихся на дневном отделении)
1. Для каких пределов вы воспользуетесь правилом вынесения постоянного множителя за знак предела:
a)[
]
b)[
]
c)[
]
d)[
]
e)[
]
2. Укажите первый замечательный предел:
a)(
)
b)(
)
c)(
)
d)(
)
3.
Чему
равен предел функции
при
:
a)(
)
b)(
)
c)( )1
d)( )0
4. Чему равен предел функции при :
a)( )e
b)( )1
c)( )0
d)( )ln2
5. Чему равен предел функции при :
a)( )0
b)( )1/2
c)( )1/8
d)( )1
6. Чему равен предел функции при :
a)( )0
b)(
)
c)( )2/5
d)( )-2/5
7. Установите соответствие между пределом функции и способом взятия предела от двух функций:
|
|
|
Предел дроби |
|
|
|
Предел разности двух функций |
|
|
|
Предел произведения двух функций |
|
|
|
Предел суммы двух функций |
8. Установите соответствие:
|
|
|
|
|
|
|
0 |
9. Установите соответствие:
|
|
|
-1/3 |
|
|
|
9/5 |
|
|
|
0 |
|
|
|
0,5 |
|
|
|
|
10.
Предел
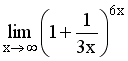равен
…
a)(
)
b)( )
c)( )1
d)(
)
11.
Количество
точек разрыва функции
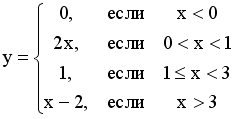равно…
a)( )3
b)( )0
c)( )2
d)( )1
12.
Какое
из указанных промежуточных решений
взятия производной по определению от
функции
является
верным?
a)(
)
b)(
)
c)(
)
d)(
)
13.
Какое
из указанных решений является верным
для взятия производной от функции
?
a)(
)
b)(
)
c)(
)
d)(
)
14.
Какое
из указанных решений является верным
для взятия производной от функции
?
a)(
)
b)(
)
c)(
)
d)(
)
15.
Вычислить
производную и найти ее значение:
,
?
a)(
)
b)(
)
c)(
)
d)(
)
16. Какие из указанных функций относятся к сложным:
a)[
]
b)[
]
c)[
]
d)[
]
e)[
]
17. К каким из данных функций вы будете применять формулу производной частного двух функций:
a)[
]
b)[
]
c)[
]
d)[
]
e)[
]
18.
Какое
из указанных решений является верным
для производной от функции
:
a)(
)
b)( ) у'=3(a-bx2)2(-2bx)
c)(
)
d)(
)
19.
Производная
функции
имеет
вид …
a)(
)
b)(
)
c)(
)
d)(
)
20.
Производная
второго порядка функции
равна
…
a)(
)
b)(
)
c)(
)
d)(
)
21. Найдите вертикальную асимптоту функции у = 5/ (x-9).
a)( ) x=9
b)( ) x=-9
c)( ) x=3
d)( ) x=-3
e)( ) x=0
22. Найдите наклонную асимптоту функции у= 2х/ (x+5).
a)( ) у=3
b)( ) у=-5
c)( ) у=2
d)( ) у=0
e)( ) у=5
23.
Уравнение
наклонной асимптоты графика функции
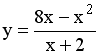имеет
вид
.
Тогда значение k равно…
a)( )4
b)( )-1
c)( )1
d)( )-2
24. Найдите интервал возрастания функции у= х2- 3х +5.
a)( )(-∞; 3)
b)( )(0; +∞)
c)( )(-1,5; +∞)
d)( )(1,5; +∞)
e)( )(-7; 7)
25. Найдите интервал убывания функции у = 0,5х2 +5х+17.
a)( )(0; 5)
b)( )(5;+∞)
c)( )(-∞;-5)
d)( )(-∞; 5)
e)( )(-5; +∞)
26.
При
прямолинейном движении точки зависимость
пути от времени задана уравнением
.
Найти ускорение точки в конце четвёртой
секунды.
a)( )1/32
b)( )1/8
c)( )-1/32
d)( )-1/8
27.
Найти
максимальное значение прибыли
в зависимости от объёма производства
:
a)( )2
b)( )4
c)( )26
d)( )16
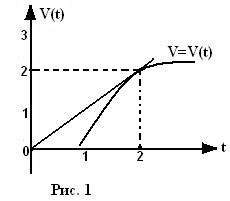
28.
Скорость
движения описывается уравнением
(рис.1). Найти ускорение при
.
a)(
)
b)( )2
c)( )1
d)( )0
29.
Проволока
длиной
согнута в прямоугольник. Каковы размеры
этого прямоугольника, если площадь его
наибольшая?
a)( )l/4*l/4
b)( )l/4*l/2
c)( )l/2*l/2
d)( )l/2*l/4
30.
Найти
промежутки выпуклости и вогнутости
графика функции
.
a)( )(-∞;0)- выпукла, (0;∞) – вогнута
b)( )(-∞;0)- вогнута, (0;∞) – выпукла
31.
Применить
правило Лопиталя для вычисления предела
a)( )0,5
b)( )1
c)( )0
d)( )-0,5
32. Установите соответствие между функцией и способом взятия производной от этой функции:
|
|
|
производная суммы |
|
|
|
производная сложной функции |
|
|
|
производная произведения двух функций |
|
|
|
производная частного |
33.
Найти
производную 2-ого порядка для функции
a)( )20х3- 48х2+30х
b)( )30х3- 48 х2+20х
c)( )20х3- 48 х2+20х
34. Производная от константы равна ?
a)( )1
b)( )0
c)( )-1
35. Операция нахождения производной называется
a)( )дифференцированием
b)( )интегрированием
c)( )частотным разложением
d)( )дифференциацией
36.
Частная
производная второго порядка
функции
равна
…
a)(
)
b)(
)
c)(
)
d)(
)
37.
Множество
первообразных функции
равно
…
a)(
)
b)(
)
c)(
)
d)(
)
38.
Вычислить
определённый интеграл
a)( )е
b)( )1-е
c)( )е-1
d)( )1
e)( )0
39.
Определённый
интеграл
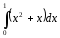равен
a)( )1/3
b)( )5/6
c)( )½
d)( )2/3
e)( )1
40.
Чему
равен определённый интеграл
?
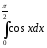a)( )0
b)( ) π/2
c)( )½
d)( )-1
e)( )1
41. Какой из интегралов берётся с помощью непосредственного интегрирования:
a)(
)
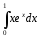
b)(
)
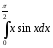
c)(
)
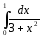
d)(
)
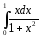
42. Какой из интегралов берётся с помощью подстановки:
a)(
)
b)(
)
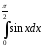
c)(
)
d)(
)
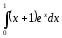
43. Для какого из интегралов следует применить интегрирование по частям
a)(
)
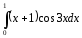
b)(
)
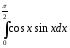
c)(
)
d)(
)
44.
При
отыскании площади плоской фигуры,
ограниченной линиями
и
,
какими будут пределы интегрирования:
a)(
)
,
b)(
)
,
c)(
)
,
d)(
)
,
e)(
)
,
45.
Какой
будет подынтегральная функция при
вычислении длины дуги кривой
от
до
a)(
)
b)(
)
c)(
)
d)(
)
e)(
)
