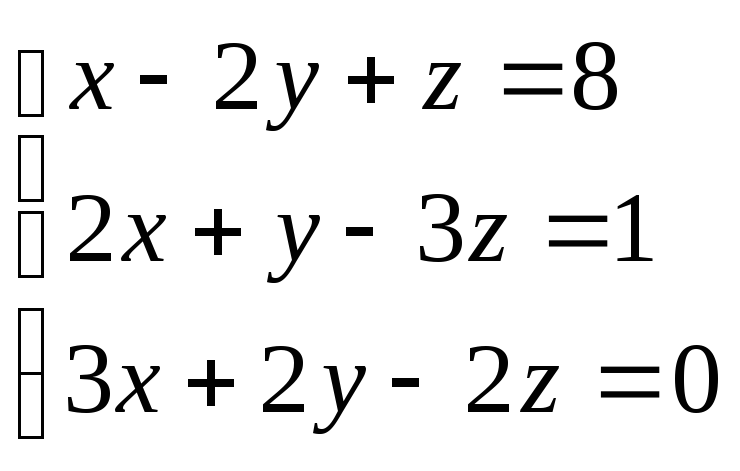Тема 1. Решение систем линейных уравнений.

Данко, гл 4,§1-7

Лихолетов, ч Iгл. 7, §58-61.

1. Системы двух уравнений 1-ой степени с двумя переменными. Определители 2-го порядка.

Пусть требуется решить систему

(1)

После исключения переменной y из уравнений получим (2).

После исключения переменной x из уравнений получим (3)

Если знаменатель , то система (1) имеет единственное решение, которое находится по формулам (2),(3).

Если принять обозначения:

, то решение системы примет вид : , (4)

, где - определители системы,- главный определитель.

Определитель- таблица, составленная из коэффициентов при неизвестных и свободных членов системы (1).

Определитель, имеющий две строки и два столбца называется определителем 2-го порядка. Формулы (4) называются формулами Крамера.

Вычисление определителей второго порядка:

(+)

(-)

Пример: =(-2·3)-(4·(-5))= -6+20=14,

2. Вычисление определителей 3-го порядка. Правило треугольников.

, т. е

Определитель 3-го порядка равен сумме произведений трёх элементов, взятых по одному из каждой строки и каждого столбца.

Пример. = ((-1)·1·(-1)+2·2·3+2·(-3)·3)-(3.1·3+2·2·(-1)+2·(-3)·(-1))= (1+12-18)- (9-4+6)=

= (-5)-11= -16.

3. Разложение определителя по элементам 1-ой строки.

=

т.е значение определителя равно произведению элементов 1-ой строки на соответствующие определители 2-го порядка, полученные после вычёркивания -той строки и-того столбца, на пересечении которых находится соответствующий элемент, причёмa₁ берётся со своим знаком,a₂-cпротивоположным,a₃- со своим знаком.

Пример: Вычислить определитель.

-1 2 3

2 1 –3 = -1 -2+3= -1·(-1+6)-2(-2+9)+3(4-3)= -1·5-2·7+3·1= -16

3 2 -1

Замечание. Разложение можно выполнять по элементам любой строки (столбца).

Задача.Решить систему

Решение: Составим главный определитель системы из коэффициентов при неизвестных и вычислим его:

= 1· - (-2)+1·= (-2+6)+2(-4+9)+1(4-3)=4+10+1=15

Составим вспомогательный определитель . Он получается из главного путём замены первого столбца свободными членами.

= 8· +2+1= 8(-2+6)+2 (-2-0)+1(2-0)=8·4+2·(-2)+2=30

Составим определитель , путём замены 2-го столбца (в главном определителе) свободными членами.

= - 45 Вычислить самостоятельно.

Составим определитель путём замены 3-го столбца (в главном определителе) свободными членами.

= =0 Вычислить самостоятельно.

Тогда по правилам Крамера имеем

, или,,

Сделать проверку самостоятельно.

Ответ: x=2, y= -3, z =0

4. Решение систем линейных уравнений методом Гаусса.

Пусть дана система 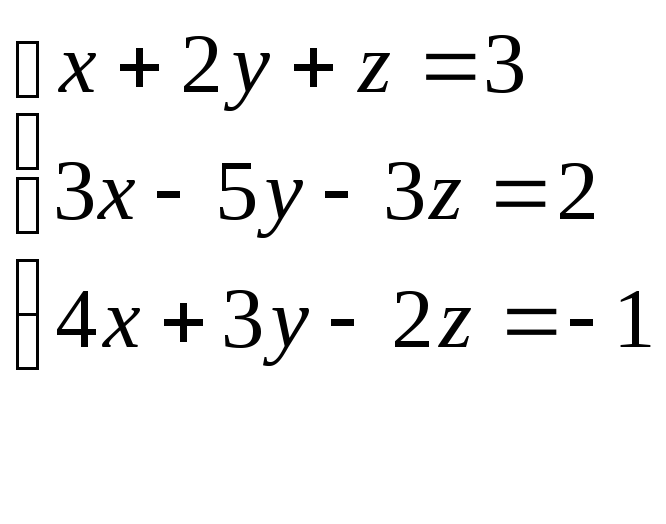(1)

Гаусс при решении системы использовал метод исключения неизвестных. В результате исходная система приводится к треугольному виду:

(2)

В этих таблицах, называемых матрицами, должны быть записаны коэффициенты при неизвестных, а после вертикальной черты-свободные члены.

В системе (2) из последнего уравнения находится неизвестное z, из 2-го-другое неизвестноеy, из 1-го- первое неизвестноеx.

Задача.Решить систему.