Тема 14. Элементы линейного программирования

[2] гл. XXVI § 3.

Задача 23. Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4000 руб., пятитонно­го - 5000 руб. Сколько нужно приобрести автомашин каж­дой марки, чтобы их суммарная грузоподъемность была мак­симальной, если для приобретения автомашин выделено 150 тысяч рублей? Задачу решить графическим и аналитиче­ским методами.

Решение. Пусть приобретено х₁ трехтонных и х₂ пяти­тонных автомашин. Из условия задачи имеем

(1)

Суммарная грузоподъемность приобретенных грузовиков равна

(2)

Задача состоит в нахождении такого решения системы (1), при котором линейная форма (целевая функция) (2) прини­мает наибольшее значение

Графический метод решения

В прямоугольной системе координат построим мно­гоугольник ОАВСD, образованный прямыми (OD), (АВ), (АО), (СD) , (ВС) и прямую(L) (рис.9).

Системе (1) удовлетворяют координаты точек, лежащих на пятиугольнике ОАВСD и внутри него. Так как прямые (L) и ВС не параллельны, то для нахождения оптимального реше­ния системы (1), для которого линейная форма (2) прини­мает наибольшее значение, достаточно найти значения этой формы в точках А, В, С, D и из полученных чисел выбрать наибольшее. В нашей задаче эти точки имеют следующие координаты: А(20; 0), В(20; 14), С(15; 18), D(0; 18). Подставляя координаты этих точек в (2), получим:

L(A)=L(20;0)=60; L(В)=L(20;14)=130;

L(С)=L(15;18)=135; L(D)=L(0;18)=90.

Р и с. 9

Следовательно, L_max=L(15;18)=135, то есть предприятию

следует приобрести 15 трехтонных и 18 пятитонных автома­шин.

Аналитический метод решения

В систему (1) введем дополнительные неизвестные х₃ и х₄, чтобы она приняла следующий вид:

₍₃₎

Система (3) имеет 3 уравнения и 4 неизвестные. Примем, на­пример,х₁ , х₂, х₃ за базисные неизвестные, а х₄ — за свобод­ное неизвестное и выразим из системы (3) неизвестные х₁ , х₂, х₃ через х₄. Тогда

, ,и

L=.

Из последнего выражения следует, что L принимает наиболь­шее значение при х₄ =0 (так как х₄0). При х₄ = 0 имеем:

_,и L(15;18)=135.

Следовательно, предприятие должно приобрести 15 трех­тонных и 18 пятитонных автомашин при их общей грузоподъ­емности 135 тонн.

Вопросы для самопроверки

1. Сформулируйте основную задачу линейного програм­мирования. Приведите примеры.

2. Дайте геометрическую интерпретацию основной задачи линейного программирования.

3. В чем суть симплекс-метода решения задач линейного программирования?

Задачи для контрольных работ Контрольная работа № 1

В задачах 1—20 даны вершины треугольника АВС.

Найти: 1) длину стороны АВ 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радиа­нах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диа­метр; 6) систему линейных неравенств, определяющих тре­угольник АВС.

1. A(—5; 0), B(7; 9), C(5; —5).

2. А(—7; 2), B(5; 11), C(3; —3).

3. А(—5; —3), B(7; 6), С(5; —8).

4. A(—6; —2), B(6; 7), C(4; -7).

5. A(—8; —4), B(4; 5), C(2; —9).

6. А (0; —1), B(12; 8), C(10; —6).

7. A(—6; 1), В(6; 10), C(4; —4).

8. A(—2; —4), B( 10; 5), C(8; —9).

9. A(—3; 0), B(9; 9), C(7; —5).

10. A(—9; —2), B(3; 7), C(1; —7).

11. A(— 5; 2), B(7; -7), C(5; 7).

12. А(—7; 5), B(5; —4), C(3; 10).

13. A(—7; 1), B(5; —8), C(3; 6).

14. А(0; 3), B(12; —6),C(10; 8).

15. А(—8; 4), В(4; -5), C(2; 9).

16. А(—2; 2), B(10; —7), C(8; 7).

17. A(1; 2), B(13; —7), C(11; 7).

18. А(—4; 1), B(8; —8), C(6; 6).

19. А(—7; —1), В (—5; —10), C(3; 4).

20. А(—3; 3), B(9; —6), C(7; 8).

В задачах 21—25 составить уравнение линии, для каждой точки которой отношение расстояний до точки А(;у) и до прямой х=а равно числу е. Полученное уравнение привести к простейшему виду и построить кривую.

21. А(4; 0), а = 9, е=.

22. А(-8; 0), а =-2, е = 2.

23. А(4; 0), а=1, е=2.

24. А(9;0), а =-4, е=1,5.

25. А(-1;0), а=-4, е=.

В задачах 26—30 составить уравнение линии, для каждой точки которой ее расстояние до точки А() равно рас­стоянию до прямой у=b. Полученное уравнение привести к простейшему виду и построить кривую.

26. А(2;1), b=-1. 27. А(-2;-2), b=-4.

28. А(2;-1), b=2. 29. А (2;-1), b=1.

30. А(4;-1), b=1.

В задачах 31—40 даны координаты точек А, В, С. Требует­ся: 1) записать векторы и в системе орт и найти модули этих векторов; 2) найти угол между векторами и ;3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору .

31. А (7; —4; 1), В(12; —3; 1), С(10; 1; 5).

32. А (0; —3; 3), В(5; —2; 3), С(3; 2; 7).

33. А (—2; —1; —2), В(3; 0; —2), С(1; 4; 2).

34. А (-6; 0; 0), В(-1; 1; 0), С(—3; 5; 4).

35. А (-2; -3; -8), В(3; -2; -8), С(1; 2; -4).

36. А(,1; 0; -1), В(6; 1; -1), С(4; 5; 3).

37. А (-1;.4;1), В(4;5;1), С12; 9; 5).

38. А (3; -6; -3), В(8; —5; —3), С(6; — 1; 1).

39. А (1; 0; 0), В(6; 1; 0), С(4; 5; 4).

40. А.(2; -8; -2), В(7; -7; -2), С(5; -3; 2).

В задачах 41—50 дамы векторы ,,,. Показать, что векторы ,,образуют базис трехмерного пространства :и найти координаты вектора в этом базисе.

41. (2;1;3),(3;-2;1),(1;-3;-4),(7;0;7).

42. (5;3;1),(-2;-1;2),(-2;1;4),(3;0;1).

43. (1;3;5),(-2;-1;-1),(4;-2;4),(-7;3;-1).

44. (3;1;6),(-2;2;-3),(-4;5;-1),(3;0;1).

45. (4;1;4),(-2;-1;1),(3;1;5),(-3;-2;1).

46. (1;2;5),(2;-3;4),(1;-1;-2),(3;0;1).

47. (5;1;2),(3;4;-1),(-4;2;1),(-3;5;4).

48. (2;1;5),(-4;3;5),(1;-1;-4),(4;-1;-3).

49. (3;1;4),(-4;2;3),(2;-1;-2),(7;-1;0).

50. (1;4;2),(5;-2;-3),(-2;-1;1),(-3;2;4).

В задачах 51—60 систему уравнений зависать в матричной форме и решить ее с помощью обратной матрицы.

51. 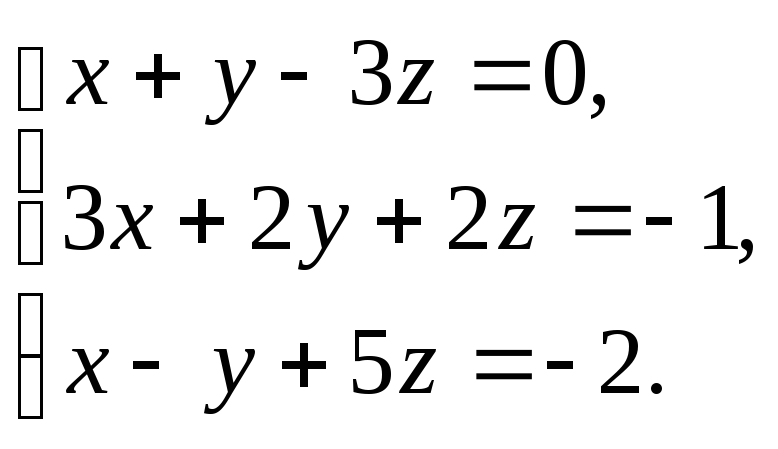52.

53. 54.

55. 56.

57. 58.

59. 60.

В задачах 61—80 найти указанные пределы.

61. а) ; б);

в) ; г).

62. а) ; б);

в) ; г).

63. а) ; б);

в) ; г).

64. а) ; б);

в) ; г).

65. а) ; б);

в) ; г).

66. а) ; б);

в) ; г).

67. а) ; б);

в) ; г).

68. а) ; б);

в) ; г).

69. а) ; б);

в) ; г).

70. а) ; б);

в) ; г).

71. а) ; б);

в) ; г).

72. а) ; б);

в) ; г).

73. а) ; б);

в) ; г).

74. а) б);

в) ; г).

75. а) ; б);

в) ; г).

76. а) ; б);

в) ; г).

77. а) ; б);

в) ; г).

78. а) ; б);

в) ; г).

79. а) ; б);

в) ; г).

80. а) ; б);

в) ; г).