
- •Линейная алгебра Математический анализ Теория вероятностей и математическая статистика
- •Рецензент
- •Тема 1. Аналитическая геометрия на плоскости
- •Тема 2. Векторная алгебра и аналитическая геометрия в пространстве
- •Тема 3. Элементы линейной алгебры
- •Вопросы для самопроверки
- •Тема 4. Введение в анализ
- •Тема 5. Производная и дифференциал
- •Тема 6. Приложения производной
- •Вопросы для самопроверки
- •Тема 7. Функции нескольких переменных
- •Вопросы для самопроверки
- •Тема 8. Неопределенный интеграл
- •Вопросы для самопроверки
- •Тема 9. Определенный интеграл
- •Вопросы для самопроверки
- •Указания к выполнению контрольной работы № 3
- •Тема 10. Дифференциальные уравнения
- •Вопросы для самопроверки
- •Тема II. Ряды
- •Вопросы для самопроверки
- •Указания к выполнению контрольной работы № 4
- •Тема 12. Повторные независимые испытания
- •Вопросы для самопроверки
- •Тема 13. Случайные величины и их числовые характеристики
- •Тема 14. Элементы линейного программирования
- •Вопросы для самопроверки
- •Задачи для контрольных работ Контрольная работа № 1
- •Контрольная работа №2
- •Контрольная работа №3
- •Контрольная работа № 4
- •Приложения
![]() Министерство сельского хозяйства
Российской Федерации
Министерство сельского хозяйства
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
“Тверская государственная сельскохозяйственная академия”
Линейная алгебра Математический анализ Теория вероятностей и математическая статистика
Методические указания и контрольные задания для
студентов заочной формы обучения.
Направление 0801000.62 - Экономика
Тверь: ТГСХА, 2013
Рецензент
Директор центра информационно – консультационного обслуживания,
заведующий кафедрой менеджмента и маркетинга в АПК ТГСХА,
д.э.н., профессор Фаринюк Ю.Т.
Рекомендованы на заседании кафедры “Математики и ВТ” _________, протокол № ____. Утверждены методической комиссией экономического факультета _________, протокол № ____.
Ганичева А.В. Линейная алгебра. Математический анализ. Теория вероятностей и математическая статистика. Методические указания и контрольные задания для студентов заочной формы обучения. Направление 0801000.62 - Экономика
В методической разработке рассмотрено решение типовых задач по каждой теме указанных курсов. Аналогичные задания предложены студентам для контрольных работ. Указан библиографический список, в конце методической разработки приведены расчетные таблицы. применение математического аппарата к задачам социально – производственной сферы.
Ю.Т. Фаринюк.
Тверь: ТГСХА, 2013
Библиографический список
1. Ефимов Н. В. Краткий курс аналитической геометрии. М.; Наука,. 1975.
2. Кудрявцев В. А., Демидович В. П. Краткий курс высшей математики. 6-е изд. М.: Наука, 1985.
3. Минорский В. П. Сборник задач по высшей математике. М.: Наука, 1977.
4. Пискунов И. С. Дифференциальное и интегральное исчисления: т. 1, 2. М.: Наука, 1978.
5. Сборник задач по математике для вузов. Линейная алгебра и основы математического анализа/Под ред. А. В. Ефимова, Б. П. Демидо- вича. М.: Наука, 1986.
6. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977.
7. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статике. М.: Высшая школа. 1975.
В настоящих методических указаниях приведенные пособия для краткости обозначаются заключенными в квадратные скобки номерами из библиографического списка. Например, запись [2] гл. 3; [3] № 66, 68, 81, 113 означает следующее: изучите материал, изложенный в главе 3 учебника Кудрявцева В. А., Демидовича В. П. «Краткий курс высшей математики» и решите задачи № 66, 68, 81, 113.из задачника Минорского В. П.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1
Тема 1. Аналитическая геометрия на плоскости
[1] гл. I, П; [3] № 4, 10, 23, 28;
[1] гл. III § 11, 12, гл. IV; [3] № 59, 67, 71, 82 (2), 87, 103;
[1] гл. V § 24—26, 30—36; [3] № 140, 155, 166, 169, 190, 211, 224.
Разберите решения задач 1, 2, 3 из данных методических указаний.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Даны вершины треугольника АВС:А(—4; 8), В (5; —4), С( 10; 6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АСи их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СDи ее длину; 5) уравнение окружности, для которой высота СDесть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
Решение: 1. Расстояние dмежду точками М1 (х1; у1) и М2(х2; у2)определяется по формуле
d=![]()
![]()
![]() (1)
(1)
Подставив в эту формулу координаты точек А и В, имеем:
АВ=![]() .
.
2. Уравнение прямой, проходящей через точки М1 (х1; у1) и М2(х2; у2) имеет вид:
![]() (2)
(2)
Подставив в (2) координаты точек А и В, получим уравнение прямой А В :
![]() ,
,  ,
,![]() ,
,
Зу—24 = —4х— 16, 4х+3у—8 = 0 (АВ).
Для нахождения углового коэффициента RАВпрямой АВ разрешим полученное уравнение относительно у:
![]()
Отсюда RАВ=-![]() .
Подставив в формулу (2) координаты точек
А и С, найдем уравнение прямой АС.
.
Подставив в формулу (2) координаты точек
А и С, найдем уравнение прямой АС.
![]() ,
,![]() ,
,![]() ,
,
х+7у-52=0 (АС)
Отсюда RАС=-![]() .
.
3. Угол α между двумя прямыми, угловые коэффициенты которых равныR1иR2определяется по формуле:
![]() tgα=
tgα=![]() .(3)
.(3)
Угол А, образованный прямыми АВ и АС,
найдем по формуле (3), подставив в нее
R1=
RАВ=
-![]() ,
R2=
RАС=
-
,
R2=
RАС=
-![]() .
.
tgА=![]()
 ,
,
![]() А=arctg1=45
А=arctg1=45![]()
![]() 0,79
рад.
0,79
рад.
4. Так как высота СDперпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т. е.
R![]() =-
=-![]() =-
=-![]() =
=![]()
Уравнение прямой, проходящей через данную точку М 1 (х1; у1) в заданном угловым коэффициентом к направлении, имеет вид:
у-у![]() =R(х-х
=R(х-х![]() ).(4)
).(4)
Подставив в (4) координаты точки С и R![]() =
=![]() ,
получим уравнение высоты СD:
,
получим уравнение высоты СD:
у-6=![]() (х-10),
4у-24=3х-30, 3х-4у-6=0 (СD).(5)
(х-10),
4у-24=3х-30, 3х-4у-6=0 (СD).(5)
Для нахождения длины СDопределим координаты точкаD, решив систему уравнений (АВ) и (СD):
 ,
,
откуда х=2, у=0, то естьD(2; 0).
Подставив в формулу (1) координаты точек С и D, находим:
CD=![]() .
.
5. Уравнение окружности радиуса Rс центром в точке Е (a;b) имеет вид:
(х-a)![]() +(у-b)
+(у-b)![]() =R
=R![]() .(6)
.(6)
Так как СDявляется диаметром искомой окружности, то ее центр Eесть середина отрезка СD.Воспользовавшись формулами деления отрезка пополам, получим:
х![]() =
=![]() ,
у
,
у![]() =
=![]()
Следовательно, Е (6; 3) иR=![]() .
Используя формулу (6),
.
Используя формулу (6),
получаем уравнение искомой окружности:
(х-6)![]() +(у-3)
+(у-3)![]() =25.
=25.
6. Множество точек треугольника АBСесть пересечение трёх полуплоскостей, первая из которых ограничена прямой АBи содержит точку С, вторая ограничена прямой ВСи содержит точку А,а третья ограничена прямой АС ясодержит точку В.
Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВи содержащую точку С, подставим в уравнение прямой АВкоординаты точки С:
4*10+3*6-8=50>0
Поэтому искомое неравенство имеет вид:
4х+3у-8![]()
Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВСи. содержащую точку А,найдем уравнение прямой ВС, подставив в формулу (2) координаты точек Ви С:
![]() ,
,![]() ,
,![]() ,
,
2х-у-14-0 (BC).
Подставив в последнее уравнение координаты точки А, имеем: 2*(-4)-8-14=-30<0. Искомое неравенство будет 2х—у—14≤0. Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АСи содержащую точку В: 5+7*(—4)—52=-75<0. Третье искомое неравенство х+7у—52≤0. Итак, множество точек треугольника АBСопределяется системой неравенств

На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АBС, высота СD, окружность с центром в точке Е.
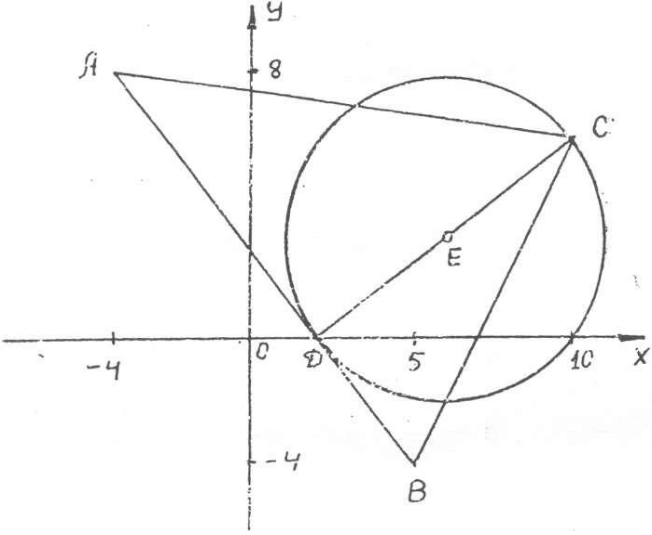
Рис.1
Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки А(3; 0) и до прямой х=12 равно числу е = 0,5. Полученное уравнение привести к простейшему виду и построить кривую.
Р е ш е н н е. Пусть М(х; у) —текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МB на .прямую х=12 (рис. 2). Тогда B( 12; у).
По условию задачи
![]() .
По формуле (1) из предыдущей задачи
.
По формуле (1) из предыдущей задачи
МА =
![]() ,
МВ=
,
МВ=![]() .
.
Тогда
![]() ,
,![]() ,
,
4х![]() ,
3х
,
3х![]()
![]() .
.
Полученное уравнение представляет собой эллипс вида
![]() где а=6,b=3
где а=6,b=3![]() .
.
Определим фокусы эллипса
F![]() (-с;0)
и F
(-с;0)
и F![]() (с;0).
Для эллипса справедливо равенство
b
(с;0).
Для эллипса справедливо равенство
b![]() ,
откуда
,
откуда
![]() и с=3.
и с=3.
То есть, F![]() (-3;0)
и F
(-3;0)
и F![]() (3;0)
- фокусы эллипса (точки F
(3;0)
- фокусы эллипса (точки F![]() и А совпадают).
и А совпадают).
Эксцентриситет эллипса
![]() =
=![]() .
.

Задача 3. Составить уравнение линии для каждой точки которой ее расстояние до точки А(3; —4) равно расстоянию до прямой у=2. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. М(х;у) —текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у=2 (рис. 3). Тогда В{х;2). Так как МА=МВ, то
![]() или
или
![]() ,
,
-12у-12=(х-3)![]() ,
,
у+1=-![]() .
.
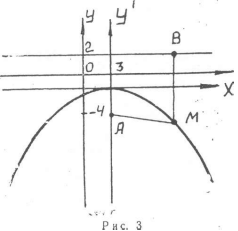
Полученное уравнение
определяет параболу с
вершиной в
точке
0 '
(3;
—1). Для
приведения уравнения
параболы
к
простейшему
(каноническому) виду положим х—3=Х',
у+1= У'. Тогда в системе
координат Х'О'У
'уравнение параболы
принимает следующий вид: У=-![]() Х')
Х')![]() .
.
В системе координат Х'О'У ' строим параболу.
Вопросы для самопроверки
Дайте определение прямоугольной декартовой системы координат.
Напишите формулу для нахождения расстояния между двумя точками.
Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении.
Напишите формулы преобразования координат: а) при параллельном переносе системы координат; б) при повороте системы координат.
Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через данную точку в данном направлении; в) проходящей через две данные точки; г) в «отрезках».
6. Как найти координаты точки пересечения двух прямых?
7. Напишите формулу для определения угла между двумя прямыми.
Каковы условия параллельности и перпендикулярности двух прямых?
Сформулируйте определение окружности.
Напишите уравнение окружности с центром в любой точке плоскости хОу ; с центром в начале координат.
Дайте определение эллипса. Напишите каноническое уравнение эллипса.
Что называется эксцентриситетом эллипса? Как изменяется форма эллипса с изменением эксцентриситета от 0 до 1?
Дайте определение гиперболы. Напишите каноническое уравнение гиперболы.
Напишите формулу для определения эксцентриситета гиперболы.
Напишите уравнения для нахождения асимптот гиперболы.
Сформулируйте определение параболы. Напишите каноническое уравнение параболы, симметричной относительно оси Оу.
