
1-й сем-ДМ-слайды-ДГТУ / Прилолжения,л.2-3
.docЛогические операции над высказываниями
-
Отрицание
Отрицание х – новое высказывание, которое истинно, если х ложно и наоборот.
-
х
х
1
0
0
1
-
Конъюнкция (логическое умножение)
Конъюнкция двух высказываний х и у – новое высказывание, которое истинно, если х и у истинно и ложно, если хотя бы одно из них ложно.
Конъюнкции х и у: х&у или x![]() у
(«х и у»).
у
(«х и у»).
-
х
у
х
 у
у1
1
1
1
0
0
0
1
0
0
0
0
-
Дизъюнкция (логическое сложение)
Дизъюнкция х и у – новое высказывание, которое истинно, если хотя бы 1 из высказываний истинно и ложно, если оба ложны.
-
х
у
х
 у
у0
0
0
0
1
1
1
0
1
1
1
1
-
Импликация – новое высказывание, логично, если х истинно, а у – ложно и истинно во всех остальных случаях.
х→у («если х, то у» или «из х следуют у»)
х – условие или посылка, у – следствие или замещение.
|
х |
у |
х→у |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
-
Эквиволенция (или эквиваленционность) двух высказываний х и у – новое высказывание, которое истинно, если оба высказывания х и у, либо одновременно истины, либо одновременно ложны и ложно во всех остальных случаях.
х→у («для того, чтобы х, необходимо и достаточно, что бы у или х тогда и только тогда, когда у»).
|
х |
у |
х |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Формулы алгебры логики:
![]()
![]() →
→![]()
![]()
|
х |
у |
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Основные равносильности
-
 закон идентичности
закон идентичности
-
 закон идентичности
закон идентичности -

-
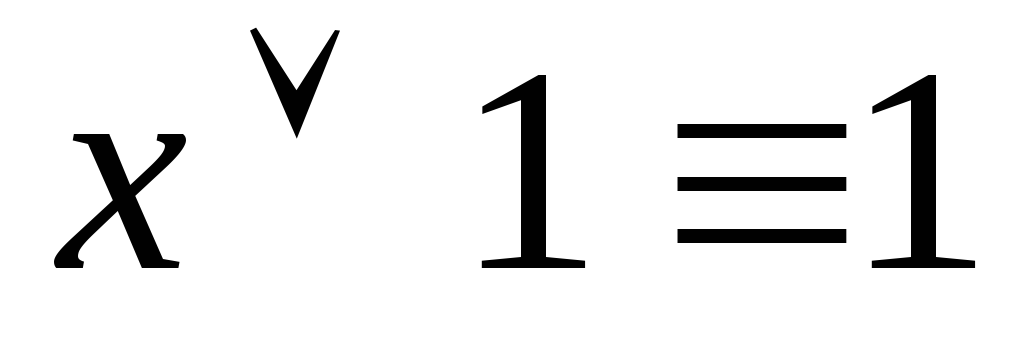
-

-
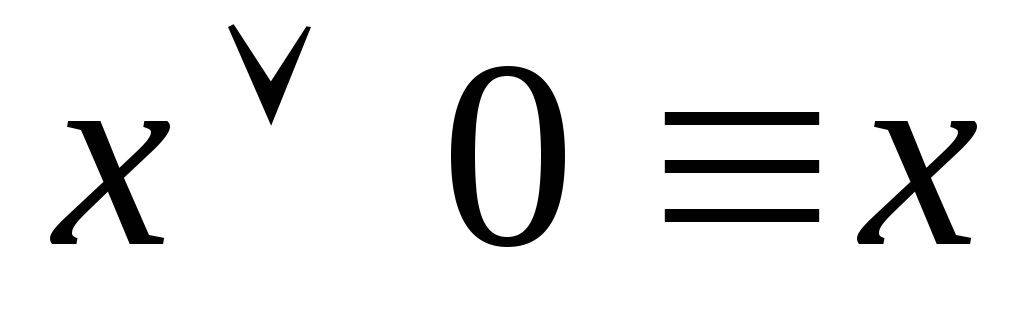
-
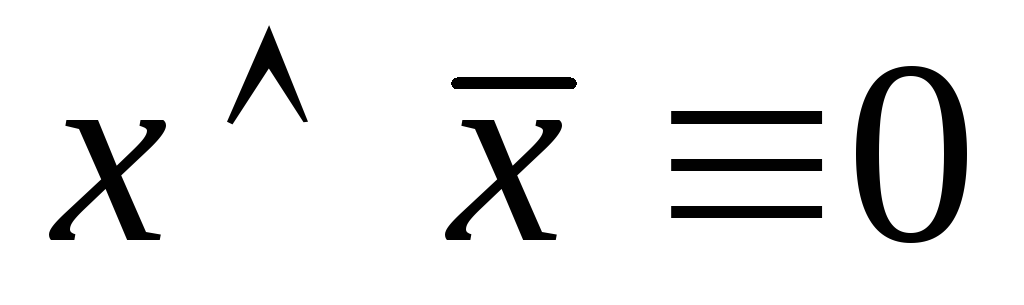 закон противоречия
закон противоречия -
 закон истинного противоречия
закон истинного противоречия -
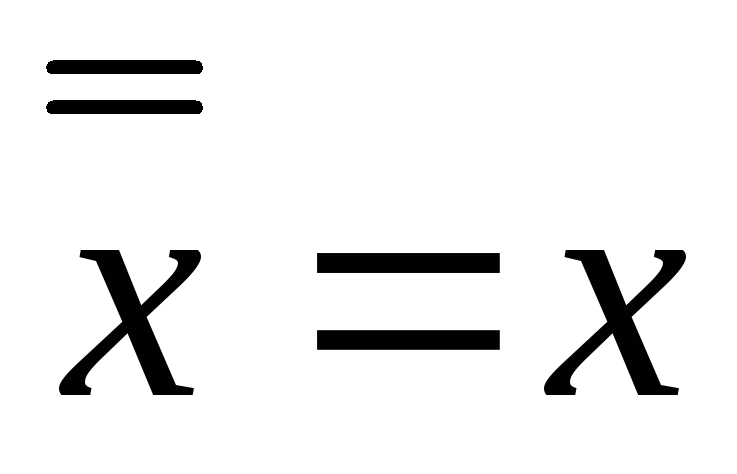 закон двойного отрицания
закон двойного отрицания -

-

Равносильности, выражающие одни логические операции через другие
Равносильности, выражающие основные законы алгебры логики
-
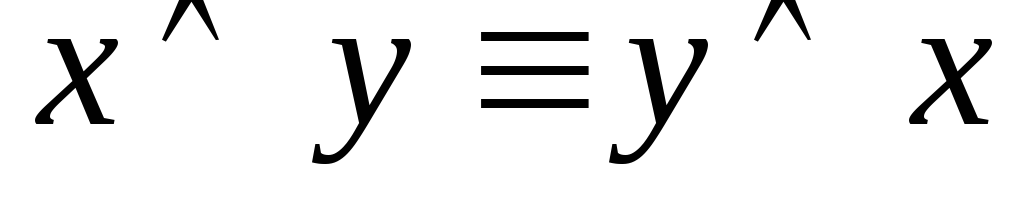 коммутативность
конъюнкции
коммутативность
конъюнкции
-
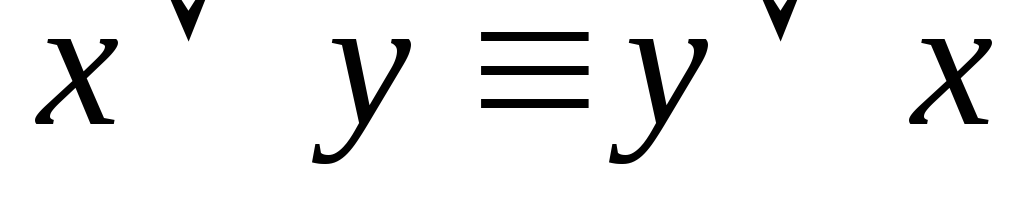 коммутативность
дизъюнкции
коммутативность
дизъюнкции
-
 ассоциативность конъюнкции
ассоциативность конъюнкции -
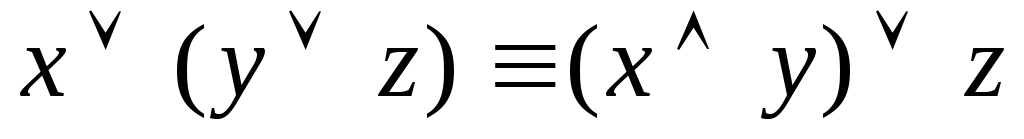 ассоциативность дизъюнкции
ассоциативность дизъюнкции -
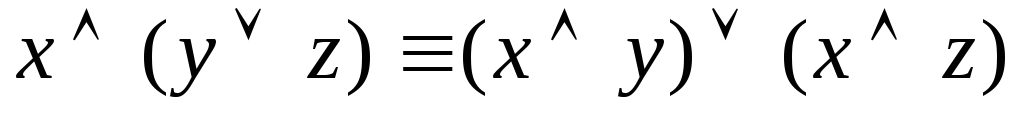 дистрибутивность конъюнкции
относительно дизъюнкции
дистрибутивность конъюнкции
относительно дизъюнкции -
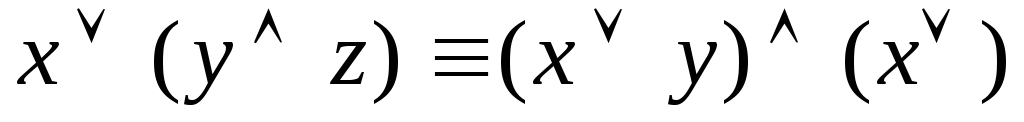 дистрибутивность дизъюнкции
относительно конъюнкции
дистрибутивность дизъюнкции
относительно конъюнкции
Булевы функции
|
x |
у |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
f16 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
f1![]() f5
f5![]() f9
f9![]() f13
f13![]()
f2![]() f6
f6![]() f10
f10![]() f14
f14![]()
f3![]() f7
f7![]() f11
f11![]() f15
f15![]()
f4![]() f8
f8![]() f12
f12![]() f16
f16![]()
Приложение:
1)
![]()
![]()
![]()






 А В
А В
![]()
![]()



2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 )
)










А




![]()
![]()




Формула:
![]()
![]()




![]()
![]()








![]()
![]()
 А
В
А
В



3) Применение алгебры логики к решению логических задач
-
Антон был вторым, а Борис – пятым
-
Виктор был вторым, а Денис – третьим
-
Григорий был первым, а Борис третьим
-
Антон был третьим, а Евгений – пятым
-
Виктор был третьим, а Евгений – четвертый
Одно из двух высказываний ошибочно. Что было на самом деле?
Обозначим высказывания ху, где х – первые буквы имени, у – номер места в структуре.
Получим:
А2![]() Б5
Б5![]() ;
В2
;
В2![]() Д3
Д3![]() ;
Г1
;
Г1![]() Б3
Б3![]() 1;
1;
А3![]() Е6
Е6![]() ;
В3
;
В3![]() Е4
Е4![]() ;
;
Тогда истинна формула:
![]()
![]() Б5)
Б5)![]() В2
В2![]() Д3)
Д3)![]() Г1
Г1![]() Б3)
Б3)![]() (А3
(А3![]() Е6)
Е6)![]() (В3
(В3![]() Е4)
Е4)![]() В2
В2![]()
![]() Д3
Д3![]() Б5
Б5![]() Д3
Д3![]() Б5
Б5![]() В2)
В2)![]() Г1
Г1![]() А3
А3![]() Г1
Г1![]() Е6
Е6![]() Б3
Б3![]() В3
В3![]() Е4)
Е4)![]() А2
А2![]() Д3
Д3![]() Г1
Г1![]() А2
А2![]() Д3
Д3![]() Г1
Г1![]() Е6
Е6![]() А2
А2![]() Д3
Д3![]() Б3
Б3![]() Е6
Е6![]() Б5
Б5![]() Д3
Д3![]() Г1
Г1![]() А3
А3![]() Б5
Б5![]() Д1
Д1![]() Г1
Г1![]() Е6
Е6![]() Б5
Б5![]() Д3
Д3![]() Б3
Б3![]() Е6
Е6![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() А3
А3![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() Е6
Е6![]() Б5
Б5![]() В2
В2![]() Б3
Б3![]() Е6)
Е6)![]() (В3
(В3![]() Е4)
Е4)![]() (А2
(А2![]() Д3
Д3![]() Г1
Г1![]() Е6
Е6![]() В3
В3![]() А2
А2![]() Д3
Д3![]() Г1
Г1![]() Е6
Е6![]() Е4
Е4![]() Б5
Б5![]() Д3
Д3![]() Г1
Г1![]() Е6
Е6![]() В3
В3![]() Б5
Б5![]() Д3
Д3![]() Г1
Г1![]() Е6
Е6![]() Е4
Е4![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() А3
А3![]() В3
В3![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() А3
А3![]() Е4
Е4![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() Е6
Е6![]() В3
В3![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() Е6
Е6![]() Е4
Е4![]() Б5
Б5![]() В2
В2![]() Г1
Г1![]() А3
А3![]() Е4.
Е4.
