Презентация по дискретной математике

на тему:

ТЕОРИЯ АВТОМАТОВ

Выполнил студент гр. ВПИ-11

Абраменков Дмитрий

Конечный автомат

Конечный автомат "в чистом виде" - это математическая модель устройства с конечной памятью, преобразующего дискретную

информацию. Конечный автомат является одним из важнейших видов управляющих систем. Содержательно конечный автомат можно

охарактеризовать как устройство, имеющее входной и выходной каналы и находящееся в каждый из моментов дискретного времени, называемых тактовыми моментами, в одном из состояний. По входному каналу в каждый тактовый момент в устройство поступают сигналы a - буквы входного алфавита A; в те же моменты по выходному каналу устройство выдает сигналы b - буквы выходного алфавита B, причем b определяется состоянием s из алфавита состояний S и буквой a; внутреннее состояние s' в следующий тактовый момент также определяется состоянием s и буквой a из предыдущего момента. Таким образом, для некоторых функций j и f имеет место равенство:

b = j ( a, s), s' = f ( a, s);

эти функции называются соответственно выходной и переходной функциями; они определяют закон переработки слов в алфавите A,

подаваемых побуквенно на входной канал устройства при условии задания начального состояния устройства.

Другие виды автоматов

Автомат "вообще" (от греческого automat oz - самодействующий) -

управляющая система, являющаяся конечным автоматом или некоторой его модификацией, полученной путем изменения его компонент или функционирования. Для конечного автомата (A, S, B, j, f) существующие модификации можно разбить на следующие три основные группы. К первой группе относятся автоматы, у которых некоторые из алфавитов A (входной), S (состояний) или B (выходной) бесконечны, в связи с чем такие автоматы называются бесконечными. Ко второй группе относятся автоматы, у которых вместо выходной и переходной функций j и f допускаются произвольные отношения или случайные функции. Таковы частичные, недетерминированные, вероятностные и другие автоматы. К третьей группе относятся автоматы со специфическими множествами входных объектов. Таковы, например, автоматы с переменной структурой. Существуют автоматы, принадлежащие одновременно разным группам. Наряду с этим большую роль играют специальные подклассы конечных автоматов, например, автоматы без памяти. Кроме того, использование понятий и методов из других разделов математики также приводит к появлению специфических классов автоматов и связанных с ними задач. Например, при применении алгебраических средств возникают понятия автоматов над термами, линейного, группового, свободного и других; вопросы теории кодирования порождают понятия самонастраивающихся, обратимых автоматов и другие.

Теория автоматов

Теория автоматов - это раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемые автоматами. С определенной точки зрения такими преобразователями являются как реальные устройства (вычислительные машины, автоматы, живые организмы и т.д.), так и абстрактные системы (например, формальная система, аксиоматические теории и т.д.). Наиболее тесно теория автоматов связана с теорией алгоритмов.

Большинство задач теории автоматов - общие для основных видов управляющих систем. К ним относятся задачи анализа и синтеза автоматов, задачи полноты, минимизации, эквивалентных преобразований автоматов и другие.

Теория автоматов находит применение как в других областях математики, так и в решении практических задач. Например, средствами теории автоматов доказывается разрешимость некоторых формальных исчислений. Применение методов и понятий теории автоматов к

изучению формальных и естественных языков привело к возникновению математической лингвистики (математическая

лингвистика - математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков).

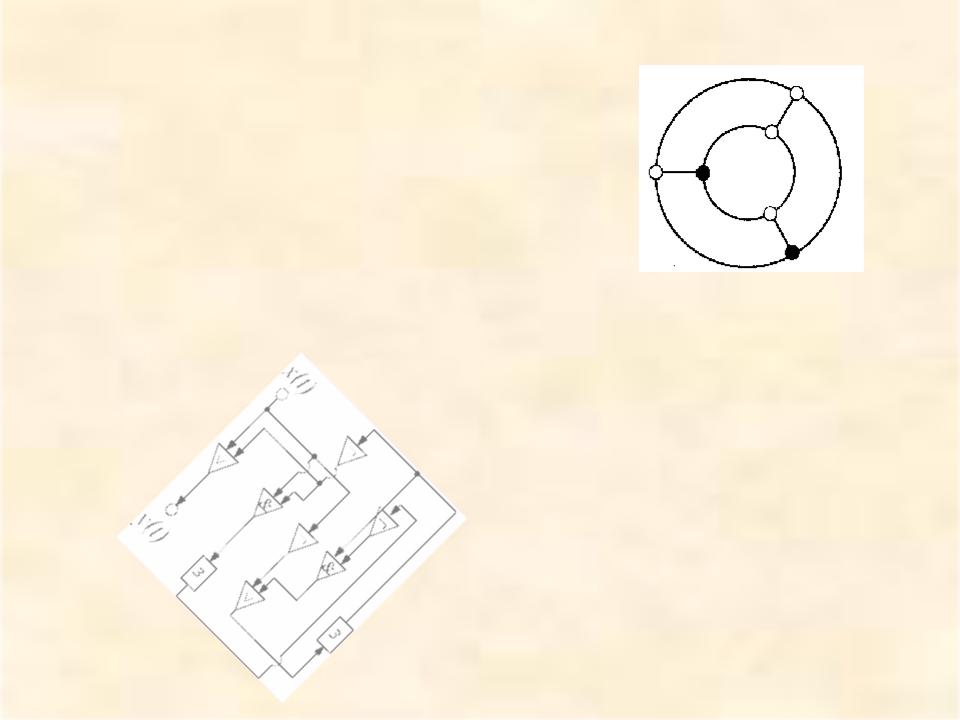
Есть два удобных способа описать этот автомат. Прежде всего, можно построить помеченный ориентированный граф, называемый диаграммой состояний.

Вершины этого орграфа помечены символами, обозначающими внутренние состояния. Каждая дуга помечена парой символов a, b, где a - входной символ, вызывающий переход в следующее состояние, отвечающее этому ребру, а b - выходной символ, который автомат выпечатывает. Второй способ описания - таблица состояний, табличное представление функций j и f. Оба способа имеют свои преимущества и недостатки. Таблица обычно удобнее при вычислениях, диаграмма нагляднее. Например, по диаграмме легче обнаружить состояния, не достижимые из других состояний. На следующем рисунке показана диаграмма состояний автомата, у которого

состояние s1 недостижимо, если автомат начинает работу из состояния s0 или s2.

Машина Тьюринга

Исторически понятие конечного автомата развилось из близкого понятия, введенного в 1936 году логиком Тьюрингом. Тьюринг рассматривал гипотетическую машину, имеющую конечное множество S внутренних состояний и одну бесконечно длинную ленту, разделенную на ячейки, которую машина могла передвигать на одну ячейку вправо или влево за такт. В каждой ячейке машина может записывать символ из конечного алфавита A. Первоначально лента должна быть пустой, кроме конечного числа ячеек заполненных заранее. (Эти заранее заполненные ячейки можно представлять себе как программу запуска машины). Основная разница между машиной Тьюринга и конечным автоматом состоит в том, что лента машины Тьюринга бесконечна и машина Тьюринга может двигаться вдоль ленты (или смещать ленту) в любом направлении. Это придает машине бесконечную память, которую можно использовать в ходе вычислений. Сверх того, каждую ячейку можно просматривать многократно.

Определение. Машиной Тьюринга называется пятерка объектов [A, S, n, z, d] следующего типа. A есть конечный алфавит символов, которые могут быть записаны в ячейках и являются одновременно входными и выходными: A = {a0, a1, . . ., an}. S есть конечное множество внутренних состояний S = {s0, s1, . . ., sr}; n - функция из S ╢ A в S; z - функция из S ╢ A в A; d - функция из S ╢ A в {П, Л, ОСТАНОВ}, интуитивный смысл которого станет ясен в дальнейшем.

Машина Тьюринга работает следующим образом. Она начинает работу, находясь в начальном состоянии s0. После считывания первого символа она переходит в новое внутреннее состояние, определяемое функцией n , записывает в ячейке символ, являющийся значением функции z , перемещает ленту направо (П), налево (Л), или остается на месте и прекращает работу (ОСТАНОВ) в зависимости от значения функции d. На рисунке схематически изображена лента машины Тьюринга и считывающе-записывающая головка.

Пример 2

Машина Тьюринга, описанная ниже, считывает входную последовательность нулей и единиц, выпечатывает Ч, если число единиц четное, и Н, если нечетно. Строке из нулей и единиц предшествуют и последуют пустые ячейки,

обозначаемые #. Символы Ч или Н печатаются в первой пустой ячейке вслед за входной строкой. Алфавит, таким образом,

имеет вид

A = {#, 0, 1, Ч, Н}.

Внутренние состояния: S = {s0, s1, s2}; s0 - начальное состояние. Машина останавливается по сигналу ОСТАНОВ.

n : (s0, 0) a s1 z: (s0, 0) a 0 d : (s0, 0) a Л (s0, 1) a s2 (s0, 1) a 1 (s0, 1) a Л

(s1, 0) a s1 (s1, 0) a 0 (s1, 0) a Л (s1, 1) a s2 (s1, 1) a 1 (s1, 1) a Л (s2, 0) a s2 (s2, 0) a 0 (s2, 0) a Л (s2, 1) a s1 (s2, 1) a 1 (s2, 1) a Л (s0,#) a s0 (s0, #) a # (s0, #) a Л

(s1,#) a s1 (s1, #) a Ч (s1, #) a ОСТАНОВ (s2,#) a s2 (s2, #) a Н (s2, #) a ОСТАНОВ