Теория графов и ее применение

Введение

В п о с л е дн е е в р е м я , и с с л е до в а н и я в о б л а с т я х ,

т р а ди ц и о н н о о т н о с я щ и х с я к ди с к р е т н о й м а т е м а т и к е , з а н и м а ю т в с е б о л е е з а м е т н о е м е с т о . Н а р я ду с т а к и м и к л а с с и ч е с к и м и р а з де л а м и м а т е м а т и к и , к а к м а т е м а т и ч е с к и й а н а л и з , ди ф ф е р е н ц и а л ь н ы е у р а в н е н и я , в у ч е б н ы х п л а н а х с п е ц и а л ь н о с т и " П р и к л а дн а я м а т е м а т и к а " и м н о г и х др у г и х с п е ц и а л ь н о с т е й п о я в и л и с ь р а з де л ы п о м а т е м а т и ч е с к о й л о г и к е , а л г е б р е , к о м б и н а т о р и к е и т е о р и и г р а ф о в . П р и ч и н ы э т о г о н е т р у дн о п о н я т ь , п р о с т о о б о з н а ч и в к р у г з а да ч , р е ш а е м ы х н а б а з е э т о г о м а т е м а т и ч е с к о г о а п п а р а т а .

ЛЕОНАРД ЭЙЛЕР (1707-1783)

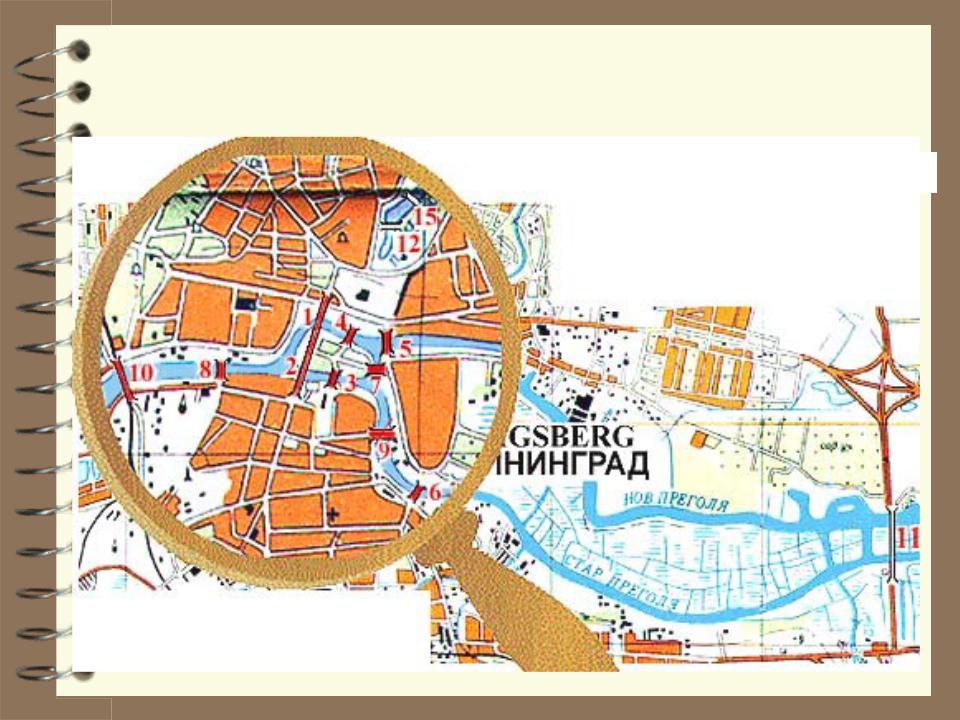
З а д а ч а Э й л е р а

Можно ли обойти все четыре части суши, пройдя по каждому мосту

один раз, и вернуться в исходную точку.

Для решения этой задачи Эйлер вводит понятие «сети» (называющейся в наше время «графом») как множества непересекающихся рёбер или связей, соединяющих пары вершин. Вот так выглядит этот граф, если наложить вершины и связи на карту города

>>>>>>В графе, имеющим более двух вершин с нечетной степенью, такого обхода не существует

П р а в и л о Э й л е р а:

1.В графе, не имеющем вершин нечетных степеней, существует обход всех рёбер (причем каждое ребро проходится в точности один раз) с началом в любой вершине графа.

2.В графе, имеющем две и только две вершины с нечетными степенями, существует обход с началом в одной вершине с нечетной степенью и концом в другой.

3.В графе, имеющим более двух вершин с нечетной степенью, такого обхода не существует

Основные понятия теории графов.

Граф - непустое множество V и X- некоторый набор пар элементов из V. Элементы множества V называются вершинами, а элементы набора X- ребрами.

Подграф - подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Остовый подграф содержит все вершины графа G.

Связный граф - граф, у которого для любых двух различных вершин существует цепь (последовательность смежных вершин), соединяющая их.

Взвешенный связный граф - связный граф, с заданной весовой функцией (каждому элементу набора X ставится в соответствие некоторое число - вес ребра).

Дерево - связный лес (граф не содержащий циклов).

Остов - остовый подграф, являющийся деревом.