
математика конспект
.pdf
Конспект лекций по курсу математики первого семестра Профессор А.В.Братищев
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ И ТЕОРИИ МНОЖЕСТВ
Под множеством будем понимать совокупность элементов, обладающим каким-либо свойством.
Обозначение Множество обозначается прописными латинскими буквами A, B, X ,... ;
элементы |
– |
строчными |
латинскими |
a, b, x, ... ; свойство |
представляет |
собой |
|||||
предложение |
или формулу |
P( x) , содержащие обозначение |
элемента. |
Запись |
|||||||
A := { x : P ( x )} |
читается |
" A |
|
по определению есть множество элементов x, которые |
|||||||
обладают свойством P( x) |
|
|
|
|
|
|
|
|
|||
ПРИМЕР |
Множество |
|
натуральных |
чисел 1, 2,... . Множество |
целых |
чисел |
|||||
|
|
|
|
m |
|
|
|
|
|
||
0, ± 1, ± 2,... . Множество := |
|
|
|
: m , n рациональных чисел (дробей). Множество |
|||||||
|
|
||||||||||
|
|
|
|
n |
|
|
|
|
|
||
действительных (вещественных) чисел R, которое состоит из множества |
|||||||||||
рациональных чисел Q и множества иррациональных чисел I. Иррациональными |
|||||||||||
являются, например, числа |
|
|
|
|
|
|
|||||
|
2 = 1, 4241..., π = 3,14159... , e = 2, 71828.. .. |
|
|
|
|||||||
ЗАМЕЧАНИЕ Действительной число рационально тогда и только тогда, когда оно представимо периодической десятичной дробью.
Определение Множество, не содержащее элементов, называется пустым. Обозначение φ .
Определение |
Множество |
B , |
все |
элементы которого принадлежат A , называется |
|
подмножеством множества |
A . |
|
|
|
|
Обозначение |
B A . Если же |
B |
является подмножеством, |
но не совпадает с A , то |
|
B A . |
|
|
|
|
|
Определение Множества A, B совпадают, если A B, B A . |
Обозначение A = B . |
||||
Определение Декартовым произведением множеств A1 , A2 ,..., An называется множество упорядоченных n -ок элементов
A1 × A2 × ... × An |
:= {(a1 , a2 ,..., an ) : a1 A1 , a2 A2 ,..., an An } . |
|
ЗАМЕЧАНИЕ Если A = ... = A =: A , то An := A × ... × A . |
||
1 |
n |
|
|
|
n |
|
|
_____ |
Определение Высказывание |
– предложение, о котором можно сказать, что оно |
|
истинно или ложно.
Обозначение Если нас интересует высказывание безотносительно к его истинности или ложности, то оно обозначается большими латинскими буквами A, B,... . Истинное
высказывание обозначается 1, а ложное - 0 . |
|
|
|
|
|
|||
Определим 5 операций над высказываниями. |
|
|
|
|||||
Определение |
Отрицанием высказывания A |
называется высказывание, которое |
||||||
истинно, если A ложно, и наоборот, ложно, если A истинно. |
||||||||
|
|
|
|
|
|
|
|
|
Обозначение |
¬A или A . Читается "неверно, что A ". |
|
|
|
||||
|
|
|
|
|
А |
|
¬А |
|
|
|
|
|
|
|
|||
Истинностная таблица операции отрицания есть |
|
|
|
|
|
|||
0 |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Определение Дизъюнкцией высказываний A, B называется высказывание, которое истинно, когда истинно или A или B , или оба вместе.
Обозначение А В. Читается " A или B ".
|
А |
В |
А В |
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
Истинностная таблица операции дизъюнкции 0 |
1 |
1 |
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
Определение Конъюнкцией высказываний A, B называется высказывание, которое истинно тогда и только тогда, когда и A и B истинны.
Обозначение A B или просто A B .Читается " A и B ".
|
А |
В |
А В |
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
Истинностная таблица конъюнкции 0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
Определение Импликацией высказываний A, B называется высказывание, которое ложно тогда и только тогда, когда A истинно, а B ложно.
Обозначение А В. Читается "если A , то B " или "из A следуетB .
|
А |
|
В |
|
А В |
|
|
|
|||
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
|
|
|
|
|
Истинностная таблица импликации 0 |
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
Определение Эквиваленцией высказываний A, B называется высказывание, которое истинно тогда и только тогда, когда A, B оба истинны или оба ложны. Обозначение A B . Читается " A тогда и только тогда, когда B ", или " A равносильно B ".
|
А |
В |
А В |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
Истинностная таблица операции эквиваленции 0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
_____
Определение Высказывание, получаемое из какой-либо группы исходных (элементарных, простых) с помощью 5 операций, называется формулой (логической). Порядок выполнения операций в формуле следующий: ←, , , , .
Порядок можно изменить расстановкой скобок.
Определение Переменные, принимающие только два значения 0 или 1, называются двоичными. Функция от n двоичных переменных, принимающая только два значения 0 или 1, называется булевой функцией.
Каждая формула порождает булеву функцию, которая задается истинностной таблицей.
Определение Формулы называются эквивалентным (равносильными), если их булевы функции совпадают. Обозначение A B .
Определение Теорема, формулируемая в форме высказывания А В называется прямой. Образованное из нее высказывание В А - обратной теоремой. Высказывание вида ←A ←B называется противоположной теоремой, а высказывание ←В ←А - теоремой, обратной к противоположной.
ЗАМЕЧАНИЕ Прямая теорема равносильна обратной к противоположной; обратная теорема равносильна противоположной.
Это следует из совпадения соответствующих таблиц истинности. |
|
|
Определение |
Методом доказательства от противного теоремы А В |
называется |
доказательство равносильной ей теоремы ←В ←А. |
|
|
Определение Теорема, формулируемая в форме А В , называется критерием. |
||
ЗАМЕЧАНИЕ Так как ( А В) ( А В) (В А) , то доказательство критерия |
||
равносильно доказательству двух теорем - прямой и обратной. |
|
|
|
_____ |
|
Определение |
Понятия, обладающие объемом с числом объектов > 1 |
называются |
предметными переменными, а их объем называется областью определения предметной переменной. Конкретные значения (реализации, интерпретации, примеры) этих понятий, а также имена собственные называются предметными постоянными. Предметные постоянные и предметные переменные называются термами.
Определение Предложение, содержащее термы, называется высказывательной функцией (предикатом), если оно становится высказыванием всякий раз, когда входящие в него предметные переменные принимают конкретные значения.
Определение Предикат называется n-местным, если он содержит n предметных переменных. Обозначение Р( X1 , ..., X n ) .
ЗАМЕЧАНИЕ 0-местный предикат естественно считать высказыванием. Определение Областью определения предиката называется множеств D значений ( x1 ,..., xn ) , которые могут принимать предметные переменные X1 , ..., X n .
Для предиката Р( X1 , ..., X n ) обозначим ({x1 ,..., xn ) D : P( x1 , ..., xn ) = 1} подмножество тех n -ок переменных, на которых этот предикат превращается в истинное высказывание.
Определение |
Квантором общности называется операция перехода от n - |
местного |
||
предиката |
Р( X1 , ..., X n ) к (n −1) -местному предикату, которая читается |
так: "для |
||
каждого xk |
Dk |
имеет место Р( X1 , ..., xk , ..., X n ) ". |
|
|
Обозначение xk Dk Р( X1 , ..., xk ,.., X n ) . |
|
|||
Определение Переменная X k |
предиката Р( X1 , ..., X n ) называется свободной, а |
|
||
исчезнувшая переменная X k |
предиката xk Dk Р( X1 , ..., xk ,.., X n ) называется |
|
||
связанной. |
|
|
|
|
Определение Квантором существования называется операция перехода от n -местного предиката Р( X1 , ..., X n ) к (n −1) -местному, которая читается так: "для некоторого xk Dk
имеет место Р( X1 ,..., xk , ..., X n ) ".
Обозначение xk |
Dk Р( X1 , ..., xk ,.., X n ) . |
ЗАМЕЧАНИЕ Над предикатами можно производить пять логических операций. |
|
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ |
|
Определение |
Матрицей размера m × n называется совокупность чисел, |
расположенных в виде таблицы из m строк и n столбцов.
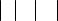
|
a11 |
... |
a1n |
|
a11 |
... |
a1n |
|
|
|
|
|
|
|
|
|
|
|
Обозначение A = |
... |
... |
... |
|
= |
... |
... |
... |
= (a |
) = |
|
|
|
a |
|
|
|
. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
ij |
|
|
|
|
|
|
... |
|
|
|
am1 |
... |
amn |
|
|
|
|
|
|
|
|
|
|
|
am1 |
amn |
|
|
|
|
|
|
|
|
|
|
|
|||||
Определение Матрицы A = (aij ), B = (bij ) называются равными, A = B , если они имеют одинаковые размеры и i j aij = bij .
Определение Матрица называется квадратной, если m = n .
Определение Диагональ квадратной матрицы, начинающаяся в левом верхнем, и оканчивающаяся в правом нижнем углу, называется главной; вторая диагональ – неглавная.
Определение Квадратная матрица называется единичной, если все числа на главной диагонали равны 1, а все числа вне главной диагонали равны 0.
Определение Матрица называется нулевой (нуль-матрица), если все ее элементы равны 0 .
Определение Суммой двух матриц A = (aij ), B = (bij ) размера m × n называется матрица
|
|
a11 + b11 |
... a1n + b1n |
|
A + B := (aij |
+ bij |
)= ............................ |
. |
|
|
|
|
|
|
|
|
am1 + bm1 |
... amn + bmn |
|
Определение Произведением матрицы A = (aij ) на число λ называется матрица
|
λa11 |
... λa1n |
|
λA := (λ aij |
)= |
.................. . |
|
|
|
λam1 |
|
|
|
... λamn |
|
Определение |
Произведением матрицы A = (aij ) размера |
m × p |
на матрицу |
B = (bij ) |
|||||
размера p × n |
называется |
|
матрица |
A B := (cij ) |
размера |
m × n , |
элементы |
которой |
|
|
|
|
|
|
|
p |
|
|
|
вычисляются по правилу cij |
= ai1b1 j + ... + aip bpj |
= ∑aik bkj . |
|
|
|
||||
|
|
|
|
|
|
k =1 |
|
|
|
Определение |
Квадратная |
матрица |
A−1 = (b |
) |
размера n × n называется обратной к |
||||
|
|
|
|
ij |
|
|
|
|
|
квадратной матрице A = (a |
) |
размера n × n , если AA−1 = A−1 A = E . |
|
|
|||||
|
ij |
|
|
|
|
|
|
|
|
_____
Определение 1 Определителем (детерминантом) первого порядка квадратной матрицы A = (a11 ) размера 1×1 называется число det A = A = a11 := a11 .
Определение 2 Определителем n -го порядка квадратной матрицы A = (aij ) размера n × n называется число
|
a11 |
... |
a1n |
n |
det A = |
... |
... |
... |
:= ai1i +1M i1 + ... + ai n (−1)i +n M i n = ∑ai k (−1)i +k M i k , |
|
an1 |
... |
ann |
k =1 |
|
|
где M i k - определитель (n − 1) -го порядка матрицы, которая получается
вычеркиванием из матрицы A i -той строки и k -го столбца.
ЗАМЕЧАНИЕ Данная формула вычисления называется разложением определителя по i - ой строке. Формула разложения по j - ому столбцу имеет вид
n
det A = ∑ak j (−1)k + j M k j = a1 j (−1)1+ j M1 j + ... + an j (−1)n+ j M n j . k =1
ТЕОРЕМА 1) Если в определителе поменялись местами две строки (два столбца), то новый определитель будет отличаться от исходного только знаком.
2)Если элементы одной строки (или столбца) умножить на одно и тоже число λ, то полученный новый определитель будет в λ раз больше исходного.
3)Если к одной строке (столбцу) прибавить поэлементно другую строку (столбец), то полученный новый определитель совпадет с исходным.
4)Пусть два определителя одинакового порядка различаются только одной строкой (столбцом). Тогда их сумма совпадает с определителем, у которого соответствующая строка (столбец) есть сумма строк (столбцов) слагаемых определителей.
Определение Минором порядка k матрицы A называется определитель матрицы, элементы которой стоят на пересечении каких-либо k строк и k столбцов матрицы A . Определение Рангом матрицы называется самый большой порядок у не равных нулю
миноров этой матрицы. Обозначение
Определение Квадратная матрица А называется невырожденной, если det A ≠ 0 , то есть когда
|
|
|
|
|
a11 ... |
|
am1 |
|
|
|
Определение Матрица |
AT = A′ := ... ... |
|
... |
называется транспонированной |
к |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1n ... |
|
amn |
|
|
|
a11 ... |
a1n |
|
|
|
|
|
|
|
|
|
матрице A = ... ... |
... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
am1 ... |
amn |
|
|
|
|
|
|
|
|
|
Определение Число |
A := |
(−1)i+ j |
M |
ij |
называется алгебраическим дополнением элемента |
|||||
|
ij |
|
|
|
|
|
|
|
|
|
a матрицы A , а матрица ( A )T |
- присоединенной матрицей к матрице A . |
|
||||||||
ij |
|
ij |
|
|
|
|
|
|
|
|
ЗАМЕЧАНИЕ Если матрица A не вырождена, |
то существует обратная матрица |
A−1 , |
||||||||
которая вычисляется по формуле A−1 = |
1 |
|
( A )T . |
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
det A |
ij |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
_____ |
|
|
||
Определение Системой линейных алгебраических уравнений (СЛАУ) |
|
|||||||||
|
|
|
|
|
a11 x1 + ... + a1n xn = b1 |
|
||||
называется система уравнений вида ................................. , где известные числа |
|
|||||||||
|
|
|
|
|
|
|
+ ... + amn xn = bm |
|
||
|
|
|
|
|
am1 x1 |
|
||||
aij , i = 1, ..., m , называются коэффициентами СЛАУ; известные числа b1 , ..., bm - |
|
|
|
|
||||||
свободными членами; неизвестные, искомые числа x1 , ..., xn |
- решением СЛАУ. |
|
|
|
||||||
a11 |
... |
a1n |
|
|
|
b1 |
|
|
|
|
Обозначения A := ... |
... |
... |
|
|
- матрица коэффициентов; B = ... - матрица |
|
|
|
||
|
... |
|
|
|
|
|
|
|
|
|
am1 |
amn |
|
|
bm |
|
|
|
|
||
|
|
x |
|
|
|
a ... |
a |
b |
|
|
|
|
1 |
|
|
11 |
1n |
1 |
|
|
|
свободных членов; |
X = ... |
|
- матрица неизвестных; |
A′ := ... ... ... |
... |
- |
||||
|
|
|
|
|
|
|
amn |
|
|
|
|
|
xn |
|
|
am1 ... |
bm |
|
|||
расширенная матрица СЛАУ.
Эти обозначения позволяют записать СЛАУ в матричном виде A X = B . Определение Решить СЛАУ – это значит найти все ее решения.
Определение СЛАУ называется совместной, если она имеет хотя бы одно решение. В противном случае СЛАУ несовместна.
Определение Две СЛАУ одинакового порядка называются эквивалентными, если они обе несовместны или обе совместны и имеют одинаковое множество решений. ЗАМЕЧАНИЕ СЛАУ переходит в эквивалентную при следующих элементарных преобразованиях: 1) перестановка местами двух уравнений,
2)умножение какого-либо уравнения на неравное нулю число,
3)поэлементное прибавление к одному уравнению другого уравнения.
Определение СЛАУ называется определенной, если она имеет ровно одно решение и неопределенной, если решений больше одного.
ТЕОРЕМА 1) (критерий Кронекера-Капелли совместности СЛАУ) СЛАУ совместна тогда и только тогда, когда ранг матрицы этой СЛАУ равен рангу расширенной матрицы.
2)(критерий определенности СЛАУ) Для того чтобы СЛАУ была определенной необходимо и достаточно, чтобы она была совместной и ранг матрицы коэффициентов совпадал с числом неизвестных: rang A = rang A′ = n.
3)(формулы Крамера) Определенная СЛАУ с помощью элементарных преобразований приводится к СЛАУ, у которой матрица коэффициентов A квадратная и det A ≠ 0 . В этом случае решение СЛАУ вычисляется по формулам
Крамера x = |
1 |
, ... , x = |
n |
, где |
:= det A, |
|
-определитель, получаемый из |
|
|
i |
|||||
1 |
|
n |
|
|
|||
заменой i-ого столбца на столбец свободных членов.
СЛЕДСТВИЕ СЛАУ с m = n будет определенной тогда и только тогда, когда rang A = n Определение Элементарными преобразованиями матрицы называются следующие: 1) перестановка двух строк;
2)поэлементное умножение какой-либо строки на неравное нулю число;
3)прибавление к одной строке соответствующих элементов другой строки. ЗАМЕЧАНИЕ СЛАУ преобразуется в эквивалентную, если ее расширенную матрицу подвергнуть элементарным преобразованиям.
Определение Методом Гаусса называется метод решения СЛАУ с помощью элементарных преобразований по следующему правилу.
АЛГОРИТМ Сначала обнуляются все элементы, стоящих ниже главной диагонали последовательно по столбцам, начиная с первого; затем обнуляют элементы над диагональю последовательно по столбцам, начиная с n -го.
_____
Определение Векторным (линейным) пространством называется множество Е, для элементов которого определены операции сложения и умножения на число, удовлетворяющие следующим аксиомам:
1)x, y E x + y = y + x,
2)x, y, z E ( x + y) + z = x + ( y + z),
3) 0 x E
4) x E (−x) E x + (−x) = 0 , 5) α , β R x E (αβ ) x = α (β x) ,
6) α , β R x E (α + β ) x = α x + β x , 7) α R x, y E α ( x + y) = α x + α y , 8) x E 1 x = x .

Определение Линейной комбинацией (линейной алгебраической суммой) элементов e1 , ..., en E называется сумма вида α1e1 + ... + αn en , где α1 ,...,αn - действительные числа, которые называются коэффициентами разложения.
Определение Элементы e1 , ..., en E называются линейно зависимыми, если существует равная нулю линейная комбинация этих элементов, в которой не все коэффициенты равны нулю. В противном случае элементы называются линейно независимыми.
СЛЕДСТВИЕ Элементы линейно зависимы тогда и только тогда, когда хотя бы один из них представим в виде линейной комбинации остальных.
Определение |
Последовательность |
элементов |
e1 ,..., en E |
называется |
полной |
(базисом) в векторном пространстве |
E если каждый элемент из Е (единственным |
||||
образом) представим в виде линейной комбинации этих элементов. |
|
||||
ТЕОРЕМА 1) |
Последовательность |
e1 ,..., en E |
является |
базисом в |
векторном |
пространстве тогда и только тогда, когда элементы e1 ,..., en линейно независимы и каждый элемент из E представим в виде их линейной комбинации.
2) Базисы в векторном пространстве имеют одинаковое число элементов. Определение Если в векторном пространстве существует базис, то число элементов n этого базиса называется размерностью пространства Е, а пространство называется n - мерным. Обозначение. dim E := n .
Определение Векторное пространство Е называется бесконечномерным, если в нём не существует базис с конечным числом элементов.
Определение Декартовым произведением векторных пространств E и F называется декартово произведение соответствующих множеств E × F := Х{x, y} : x E, y F , на котором определены операции сложения элементов и умножения их на число по правилу:
{x1 , y1} + {x2 , y2 } := {x1 + x2 , y1 + y2 }, λ{x, y} := {λ x, λ y} .
ЗАМЕЧАНИЕ 1 Введенные операции на декартовом произведении удовлетворяют 8
аксиомам. |
|
|
|
|
|
|
|
|
|
ЗАМЕЧАНИЕ 2 Аналогично определяются декартовы произведения n пространств |
|||||||||
E × ...× E |
n |
и |
E n := E × ...× E . |
||||||
1 |
|
|
|||||||
|
|
|
n |
||||||
5 развернутых важных примеров векторных пространств. |
|||||||||
ПРИМЕР 1 |
Пространство векторов с общим началом V3 . |
||||||||
ПРИМЕР 2 |
Пространство комплексных чисел . |
||||||||
|
|
|
|
|
|
|
|||
Определение Символ вида i = −1 , обладающий свойством i2 = i i = −1 −1 := −1, |
|||||||||
называется мнимой единицей. |
|||||||||
Определение Выражение вида a + bi = a + b |
−1 , |
где a, b , называется комплексным |
||
числом (в алгебраической форме). |
|
|
|
|
Обозначение |
Комплексное число традиционно обозначается буквой |
z := a + bi ; |
||
множество комплексных чисел обозначается . |
|
|
||
Определение |
Вещественное число |
a |
называется действительной |
частью |
комплексного числа z := a + bi , а вещественное |
число b называется коэффициентом |
|||
мнимой части bi комплексного числа. |
|
|
|
|
Обозначение |
Re z := a, Im z := b . |
|
|
|
Определение Комплексные числа z1 := a1 + b1i, z2 := a2 + b2 i , |
называются равными, если |
|||
равны их действительные и мнимые части: z1 = z2 |
|
a1 = a2 b1 = b2 . |
||
Определение Число вида |
0 + 0i называется |
нулём |
(комплексным) и кратко |
|
обозначается 0 . Вместо a + 0i |
обычно пишут просто a . |
|
||
Определение Суммой комплексных чисел z1 := a1 + b1i , |
z2 := a2 + b2i называется |
|||
комплексное число z1 + z2 := (a1 + a2 ) + (b1 + b2 )i .
Следующее определение несколько более общее, чем требуется в этом примере. Определение Произведением комплексных чисел z1 := a1 + b1i , z2 := a2 + b2i называется
комплексное число z1 z2 := (a1a2 − b1b2 ) + (a1b2 + a2b1 )i .
ЗАМЕЧАНИЕ 1 Множество комплексных чисел удовлетворяет аксиомам 1)-8) векторного пространства относительно операций сложения и умножения на действительной число. Две аксиомы мы уже проверили.
ЗАМЕЧАНИЕ 2 Вещественная и мнимая единицы 1, i образуют базис в . Поэтому dim = 2 .
ЗАМЕЧАНИЕ 3 В определении векторного пространство элементы умножаются на действительные числа. Аналогично определяется векторное пространство, в котором элементы умножаются на комплексные числа. В этом случае говорят о векторном пространстве над полем комплексных чисел (комплексном пространстве).
ПРИМЕР 3 Пространство M m,n матриц размера m × n .
Определения равенства матриц, нулевой матрицы, суммы матриц и произведения матриц на число мы уже давали. Из восьми аксиом проверим для множества
|
−a |
... |
−a |
|
|
|
11 |
|
1n |
|
|
M m,n , например, четвертую. Матрица − A := ... |
... ... |
|
является |
||
|
−a |
... |
−a |
|
|
|
m1 |
|
m,n |
|
|
противоположной к матрице A = (aij ) .
|
|
a |
− a |
|
... |
|
|
11 |
11 |
|
|
Действительно, |
A + (− A) = ... |
|
... |
||
|
a |
− a |
m1 |
... |
|
|
|
m1 |
|
|
|
a1n
am,n
− a |
|
0 |
|
1n |
|
|
|
... |
|
= ... |
|
|
|
|
0 |
− am,n |
|
||
... 0
... ... - нуль-матрица.
... 0
ЗАМЕЧАНИЕ Попарно различные матрицы размера |
m × n в количестве m n |
||||||||||
штук, у каждой из которых один элемент равен 1, а остальные равны 0, образуют |
|||||||||||
базис в пространстве M m,n . |
|
|
|
|
|
|
|
|
|
||
ПРИМЕР 4 Пространство P |
многочленов степени ≤ n . |
|
|
|
|
||||||
|
|
n |
|
|
|
|
|
|
|
|
|
Определение |
Многочленом |
степени |
n {0} |
называется |
функция вида |
||||||
p( x) = a |
+ a x + ... + a xn , где a ,..., a |
(или ), причем a |
n |
≠ 0 . То есть многочлен |
|||||||
0 |
1 |
n |
0 |
n |
|
|
|
|
|
|
|
является линейной комбинацией степеней 1 := x0 , x, ,..., xn |
|
|
|
|
|||||||
Определение Многочлены p( x) = a |
+ a x + ... + a xn , q( x) = b |
+ b x + ... + b xn называются |
|||||||||
|
|
|
|
0 |
1 |
n |
0 |
|
1 |
|
n |
равными, если у них совпадают коэффициенты при одинаковых |
|
||||||||||
степенях k ≤ n ak = bk |
|
|
|
|
|
|
|
|
|
||
Определение |
Многочлен 0 + 0 x + ... + 0 xn |
называется нулевым (нулем в простран |
|||||||||
стве) P и обозначается 0 .
n
Определение Суммой многочленов p( x), q( x) P называется многочлен
n
[ p + q]( x) := (a0 + b0 ) + (a1 + b1 ) x + ... + (an + bn ) xn .
Определение Произведением числа λ на многочлен p( x) = a |
+ a x + ... + a xn |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
n |
|
называется многочлен [λ p]( x) = λa + λa x + ... + λa xn . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0 |
1 |
|
n |
|
|
|
|
|
|
ЗАМЕЧАНИЕ 1 |
Множество |
P |
удовлетворяет аксиомам 1)-8), и потому является |
||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
векторным пространством. |
|
|
|
|
|
|
|
|
|
|
|
||||
ЗАМЕЧАНИЕ 2 |
Последовательность многочленов 1, x, ,..., xn |
является базисом в P . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
Поэтому dim P = n +1 . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИМЕР 5 |
Арифметическое пространство n . |
|
|
|
|
|
|
|
|||||||
n = {{a ,..., a |
n |
) : a ,..., a } |
мы |
обозначили |
множество |
упорядоченных |
n -ок |
||||||||
1 |
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
действительных чисел. |
|
|
|
|
|
|
|
|
|
|
|
||||
Определение |
Две |
n -ки {a1 ,..., an }, {b1 ,...,bn } |
называются |
равными, |
если |
числа, |
|||||||||
стоящие на одинаковых местах, совпадают: 1 ≤ k ≤ n ak |
= bk . |
|
|
|
|||||||||||
Определение Нулём в n называется |
n - ка вида {0,..., 0} . |
|
|
|
|
|
|||||||||
Определение |
Суммой двух |
n - |
ок |
a = {a1 ,..., an }, |
b = {b1 ,..., bn } |
называется |
n - ка |
||||||||
a + b := {a1 + b1 ,..., an + bn } . |
|
|
|
|
|
|
|
|
|
|
|
||||
Определение Произведением числа λ на n - ку a = {a1 ,..., an } называется |
n - ка |
|
|||||||||||||
λa := {λa1 ,..., λan } . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ЗАМЕЧАНИЕ 1 |
Множество |
n |
удовлетворяет аксиомам 1)-8), и потому является |
||||||||||||
векторным пространством. |
|
|
|
|
|
|
|
|
|
|
|
||||
ЗАМЕЧАНИЕ 2 Элементы e1 := {1, 0,..., 0}, |
e2 := {0,1, 0, ..., 0},..., en := {0,...0,1} |
|
|
||||||||||||
образуют базис в n . Следовательно, dim n = n . |
|
|
|
|
|
|
|||||||||
ЗАМЕЧАНИЕ |
3 |
Множества |
чисел |
, , |
, |
I |
не |
являются |
векторными |
||||||
пространствами.
_____
Определение Отображением множества A в множество B называется правило, сопоставляющее каждому элементу из A один элемент из B . В случае B = A отображение называется преобразованием.
Обозначение Правило обозначается латинскими буквами. Например, F : A → B . Определение Множество A называется областью определения отображения F ; множество B - областью значений отображения; множество
F ( A) := { y B : x A y = F ( x)} - множеством значений (образом отображения) F .
Определение Отображение L из векторного пространства E в векторное пространство F называется линейным оператором (отображением), если
α , β R a,b E L (α a + β b) = α La + β Lb .
Определение Линейный оператор L : E → F называется изоморфизмом векторных пространств E и F , если он переводит разные элементы в разные:
( x1 ≠ x2 ) (Lx1 ≠ Lx2 ) , и каждый элемент из F является образом некоторого элемента из E : y F x E Lx = y . При этом пространства E, F называются изоморфными. ЗАМЕЧАНИЕ 1 Это понятие позволяет формулировать результаты для векторного пространства на языке изоморфного ему пространства. Иногда это оказывается удобным.
Определение Линейный оператор из E в (C) называется линейной формой
(линейным функционалом). |
|
|
Определение Отображение F ( x ,..., x ) из векторного пространства E n |
в векторное |
|
1 |
n |
|
пространство F называется n - линейным полилинейным) отображением, если оно является линейным отображением из E в F по каждой переменной xk , k = 1,.., n , при фиксированных остальных.
Определение n - линейное отображение из En в называется n - линейной (полилинейной) формой.
ЗАМЕЧАНИЕ 2 - линейное отображение F ( x1 , x2 ) : E 2 → F принято называть билинейным отображением .
Определение Билинейная форма B( x, y) : E 2 → называется скалярным произведением на векторном пространстве E , если она обладает свойствами:
1) x, y E B( y, x) = B( x, y) ; 2) ( y E B( x, y) = 0) ( x = 0) ; 3) x ≠ 0 B( x, x) > 0
Обозначение x, y = (x, y) := B( x, y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Определение Отображение |
|
|
|
: E → , называется нормой, если оно обладает |
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
свойствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) x ≠ 0 |
|
> 0 ; |
|
2) x E λ |
|
λ x |
|
= |
|
λ |
|
x |
|
; |
3) x, y E |
|
x + y |
|
≤ |
|
x |
|
+ |
|
y |
|
. |
||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
ЗАМЕЧАНИЕ 1 |
Понятие нормы, как нетрудно заметить по свойствам, обобщает |
||||||||||||||||||||||||||||||||||||||||||||||
понятие длины вектора в V3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ЗАМЕЧАНИЕ 2 |
Каждое скалярное произведение |
x, y |
: E 2 → порождает норму в E |
||||||||||||||||||||||||||||||||||||||||||||
по правилу |
|
|
|
|
:= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
x, x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
СЛЕДСТВИЕ Естественное скалярное произведение в |
n |
обладает свойством |
|||||||||||||||||||||||||||||||||||||||||||||
R |
|||||||||||||||||||||||||||||||||||||||||||||||
|
x y |
+ ... + x y |
n |
|
≤ |
|
x2 |
+ ... + x2 |
|
y2 |
+ ... + y2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
1 1 |
|
n |
|
|
|
1 |
|
|
n |
|
1 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение n -мерным евклидовым (точечным) пространством называется тройка объектов: n -мерное векторное пространство E , какое-либо скалярное произведение  x, y
x, y  на нём и множество “точек” P , которые согласованы следующим образом:
на нём и множество “точек” P , которые согласованы следующим образом:
1) каждой упорядоченной паре точек A, B P поставлен в соответствие один элемент
x E , который обозначают x = AB ; 2) x E A P существует единственная
точка B со свойством x = AB ; 3) A, B, C P AB + BC = AC .
Обозначение = = .
E E n (E, , , P)
Определение Расстоянием между двумя точками M1 , M 2 P называется число
ρ (M1 , M 2 ) := 
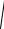
 M1 M 2 , M1 M 2
M1 M 2 , M1 M 2  =
= 
 M1 M 2
M1 M 2 
 .
.
Определение n − мерным аффинным пространством называется пара (E, P) со свойствами 1) -3).
Определение n − мерным евклидовым векторным пространством называется пара
(E, , ) .
Определение |
|
|
|
n |
называет |
n - мерным арифметическим евклидовым пространством |
|||||
ся тройка объектов: арифметическое пространство n , естественное скалярное |
|||||
произведение |
x, y := x1 y1 + ... + xn yn и множество ”точек” P := {( x1 ,..., xn ) : x1 ,..., xn } . |
||||
|
n |
свяжем с вектором из |
n |
по правилу |
|
При этом точки A = ( x1 ,..., xn ) , B( y1 ,..., yn ) |
|
||||
