
- •21. Основной закон релятивистской динамики.
- •23. Частицы с нулевой массой.
- •24. Модель идеального газа. Уравнение состояния.
- •25. Основное уравнение мкт газов.
- •28. Распределение Максвелла. Виды скоростей молекул и их физический смысл. Распределение Максвелла
- •32. Работа газа при изменении его объёма.
- •34. Применение первого начала к изопроцессам.
- •35. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
- •Адиабата Пуассона
- •36. Политропические процессы. Уравнение политропы.
- •37. Понятие энтропии. Свойства энтропии. Второе начало термодинамики.
- •38. Изменение энтропии при обратимых и необратимых процессах.
- •39. Третье начало термодинамики (теорема Нернста).
- •40. Принцип работы тепловой машины. Кпд.
- •46. Физические типы кристаллических решёток.
- •51. Теплопроводность. Внутреннее трение (вязкость).
- •52. Диффузия, теплопроводность и вязкость газов.
- •53. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции.
- •54. Поток вектора. Теорема Гаусса. Расчёт электростатических полей.
- •55. Работа сил электростатического поля.
- •56. Потенциал. Градиент потенциала. Циркуляция вектора. Эквипотенциальные поверхности.
32. Работа газа при изменении его объёма.
Найдём
в общем виде внешнюю работу, совершаемую
газом при изменении его объёма. Рассмотрим
газ в цилиндре. Под поршнем, внутри,
находится газ под давлением Р. Работа
dA
= F*dL,
p
= F/S,
F
= p*S
=> dA
= p*S*dL
= p*dV
Полную
работу, совершаемую газом, при изменении
объёма от V1
до V2,
можно определить через интеграл:А =
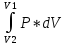
33.
Теплоёмкость газа. С
=
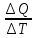 (Дж/К)
Существуют и другие
виды теплоёмкости:
1.Удельная
теплоёмкость вещества – величина,
равная кол-ву теплоты, необходимое для
нагревания одного вещ-ва на 1К. С =
(Дж/К)
Существуют и другие
виды теплоёмкости:
1.Удельная
теплоёмкость вещества – величина,
равная кол-ву теплоты, необходимое для
нагревания одного вещ-ва на 1К. С =
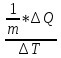 (Дж/кг*К)
2.Молярная
теплоёмкость – величина теплоты,
необходимая для нагрева 1 моля вещества
на 1К.
С =
(Дж/кг*К)
2.Молярная
теплоёмкость – величина теплоты,
необходимая для нагрева 1 моля вещества
на 1К.
С =
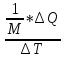 Между
молярной и удельной теплоёмкостями
есть связь: C
уд =
Между
молярной и удельной теплоёмкостями
есть связь: C
уд =
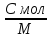 3.Различают
теплоёмкости при постоянном объёме Сv
и при постоянном давлении Ср.
Сv
=
3.Различают
теплоёмкости при постоянном объёме Сv
и при постоянном давлении Ср.
Сv
=
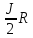 Ср.
=
Ср.
=
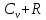
34. Применение первого начала к изопроцессам.
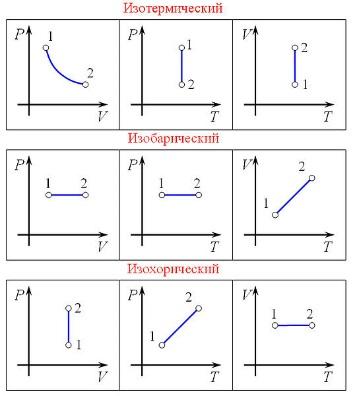
А) Изотермический процесс - процесс изменения состояния термодинамической системы при постоянной температуре
T
= const, PV = const, ∆U = const, A = RT*ln (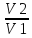 )
)
Б) Изобарный процесс - процесс изменения состояния термодинамической системы при постоянном давлении
P
= const,
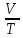 = const, ∆Q= ∆U + ∆A, A = P(V2-V1)
= const, ∆Q= ∆U + ∆A, A = P(V2-V1)
В) Изохорный процесс - процесс изменения состояния термодинамической системы при постоянном объёме
V
= const,
![]() ,
,
35. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
Адиабатический
процесс - термодинамический процесс
в макроскопической системе, при котором
система не обменивается тепловой
энергией с окружающим пространством.
Если термодинамический процесс в общем
случае являет собой три процесса —
теплообмен, совершение системой (или
над системой) работы и изменение её
внутренней энергии, то адиабатический
процесс, в силу отсутствия теплообмена
(![]() )
системы со средой сводится только к
последним двум процессам. Поэтому,первое
начало термодинамикив этом случае
приобретает вид
)
системы со средой сводится только к
последним двум процессам. Поэтому,первое
начало термодинамикив этом случае
приобретает вид![]()
где ![]() —
изменениевнутренней
энергиитела,
—
изменениевнутренней
энергиитела,![]() —работа,
совершаемая системой.
—работа,
совершаемая системой.
Адиабата Пуассона
Для идеальных
газов,
чью теплоёмкость можно считать
постоянной, в случае квазистатического
процесса адиабата
имеет простейший вид и определяется
уравнением
![]() где
где ![]() —
его объём,
—
его объём, ![]() — показатель
адиабаты,
— показатель
адиабаты, ![]() и
и ![]() — теплоёмкости газа
соответственно при постоянном давлении
и постоянном объёме.С учётом уравнения
состояния идеального газа уравнение
адиабаты может быть преобразовано к
виду
— теплоёмкости газа
соответственно при постоянном давлении
и постоянном объёме.С учётом уравнения
состояния идеального газа уравнение
адиабаты может быть преобразовано к
виду![]() где
где ![]() — абсолютная
температура газа.
Или к виду
— абсолютная
температура газа.
Или к виду![]() Поскольку
Поскольку ![]() всегда
больше 1, из последнего уравнения
следует, что при адиабатическом сжатии
(то есть при уменьшении
всегда
больше 1, из последнего уравнения
следует, что при адиабатическом сжатии
(то есть при уменьшении ![]() )
газ нагревается (
)
газ нагревается (![]() возрастает),
а при расширении — охлаждается, что
всегда верно и для реальных газов.
Нагревание при сжатии больше для того
газа, у которого больше коэффициент
возрастает),
а при расширении — охлаждается, что
всегда верно и для реальных газов.
Нагревание при сжатии больше для того
газа, у которого больше коэффициент ![]() .
.
