
- •Определители: определение, вычисление определителей 2-го и 3-го порядка. Решение слау методом Крамера.
- •Прямая на плоскости. Уравнения (вывод)
- •Плоскость. Уравнение (вывод).
- •Прямая в пространстве, уравнения (вывод).
- •Общее уравнение прямой
- •Кривые второго порядка.
- •Числовые последовательности: определение.
- •Непрерывность функции в точке. Точки разрыва, их виды, примеры. Свойства функции, непрерывной на отрезке.
- •Называется точкой разрыва первого рода:
- •Называется точкой разрыва второго рода:
- •Определение производной, её геометрический и физический смысл.
-
Непрерывность функции в точке. Точки разрыва, их виды, примеры. Свойства функции, непрерывной на отрезке.
Функция f(x)
называется непрерывной в точке
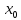 если выполняются все следующие условия:
если выполняются все следующие условия:
-
Функция определена в самой точке
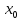 и в некоторой её окрестности.
и в некоторой её окрестности. -
Существуют односторонние пределы и они одинаковы
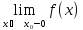 =
=
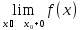
-
Односторонние пределы равны значению функции в точке

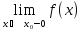 =
=
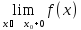 = f(x)
= f(x)
Если какое-то из
этих условий нарушено, то функция терпит
разрыв в точке
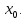
 – точка разрыва.
– точка разрыва.
Классификация точек разрыва:
-
Называется точкой разрыва первого рода:
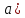 если
существуют конечные числовые односторонние
пределы функций в этой точке, но они не
совпадают.
если
существуют конечные числовые односторонние
пределы функций в этой точке, но они не
совпадают.
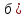 если существуют
конечные числовые равные односторонние
пределы функции f(x)
в точке
если существуют
конечные числовые равные односторонние
пределы функции f(x)
в точке
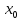 ,
но они не совпадают со значением функции
в точке
,
но они не совпадают со значением функции
в точке
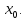 В этом случае разрыв называется
устранимым, так как его можно искусственно
устранить, доопределяя функцию
соответствующим образом.
В этом случае разрыв называется
устранимым, так как его можно искусственно
устранить, доопределяя функцию
соответствующим образом.
-
Называется точкой разрыва второго рода:
Если хотя бы один из односторонних пределов не существует или равен бесконечности.
Функцию f(x) называют непрерывной на отрезке [а, b], если она непрерывна в каждой точке интервала (а, Ь) и, кроме того, непрерывна справа в точке а и непрерывна слева в точке b.
Свойства функции:
-
О большем и наименьшем значении. Если функция f(x) непрерывна на отрезке [а, b], то на этом отрезке она достигает своих наибольшего (М) и наименьшего (м) значений.
-
О промежуточном значении. . Если функция f(x) непрерывна на отрезке [а, b] и на концах отрезка принимает значения разных знаков, то в интервале (a;b) найдется хотя бы 1 корень. То есть существует x = С, принадлежащее (a;b), такая, что f( c ) = 0
-
Определение производной, её геометрический и физический смысл.
Пусть
функция y=f(x)
определена и непрерывна в точке
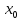 ,
принадлежащей
области определения функции и её
окрестностям. Дадим
,
принадлежащей
области определения функции и её
окрестностям. Дадим
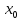 малое
приращение ∆х и получим
малое
приращение ∆х и получим
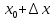 .
Найдем
приращение функции. Рассмотрим отношение
.
Найдем
приращение функции. Рассмотрим отношение
 .
Конечный
предел отношения приращения функции
.
Конечный
предел отношения приращения функции
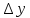 к приращению аргумента
к приращению аргумента
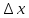 при условии, что
при условии, что
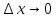 ,
называется производной функции f(x)
в точке
,
называется производной функции f(x)
в точке
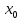 .
.
Физический смысл производной: если функция y=f(x) описывает какой-либо физический процесс, то производная – есть скорость протекания этого процесса.
Геометрический
смысл производной: Производная
функции y = f(х) при х =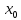 равна угловому коэффициенту касательной
к графику данной функции в точке Мо(хо,
f(xо)), т. е.
равна угловому коэффициенту касательной
к графику данной функции в точке Мо(хо,
f(xо)), т. е.
![]()
Уравнение
касательной к плоской кривой: уравнение
касательной – уравнение прямой,
проходящей через точку (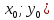 c
угловым коэффициентом k
= f(
c
угловым коэффициентом k
= f(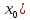 .
.

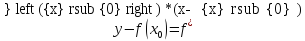
Уравнение
нормали к кривой: нормалью
к данной кривой в точке
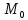 называется прямая, проведенная через
называется прямая, проведенная через
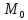 ,
перпендикулярно к кривой.
,
перпендикулярно к кривой.
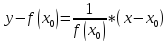
Критерий
непрерывности функции в терминах
приращений. Чтобы
функция y = f(х) была непрерывная в точке
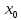 ,
необходимо и достаточно выполнения
условия -
,
необходимо и достаточно выполнения
условия -
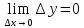 .
.
Теорема
о связи непрерывности функции с наличием
производной. Если
функция f(x)
в точке
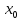 имеет производную
имеет производную
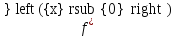 ,
то функция f(x)
непрерывная в точке
,
то функция f(x)
непрерывная в точке
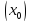 .
.
Доказательство:
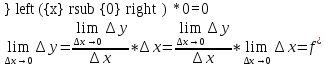
Производная
сложной функции: пусть
функция u
= ϕ (x)
имеет производную в точке
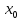 ,
то есть
,
то есть
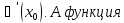 y=f(u)
имеет производную f’(
y=f(u)
имеет производную f’(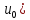 ,
где
,
где
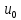 – значение
– значение
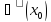 .
Тогда композиция этих функций будет
выглядеть так: y
=
.
Тогда композиция этих функций будет
выглядеть так: y
=
 .
.
Также справедлива формула:
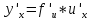 .
.
Производная сложной функции равна произведению производной внешней функции по своему аргументу на производную внутренней функции по её аргументу.
Производная
обратной функции: пусть
функция y=f(x)
имеет производную
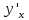 .
И у этой функции существует непрерывная
обратная функция x=g(y),
которая имеет производную. Тогда g’(y)
=
.
И у этой функции существует непрерывная
обратная функция x=g(y),
которая имеет производную. Тогда g’(y)
=
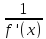 .
.
Правила вычисления производной:
Пусть функция g(x) и f(x) имеют производные g’(x) и f’(x). Тогда:
-
(const)’ = 0
-
(x)’=1
-
(f+g)’ = f’ + g’
-
(f*g)’ = f’g + fg’
-
(
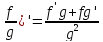
-
(const *f)’ = const *f’
Производные элементарных функций (выводы).


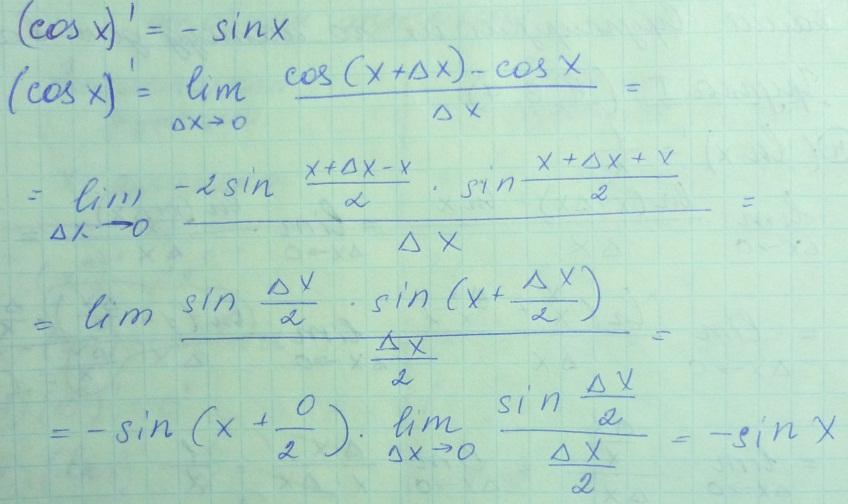
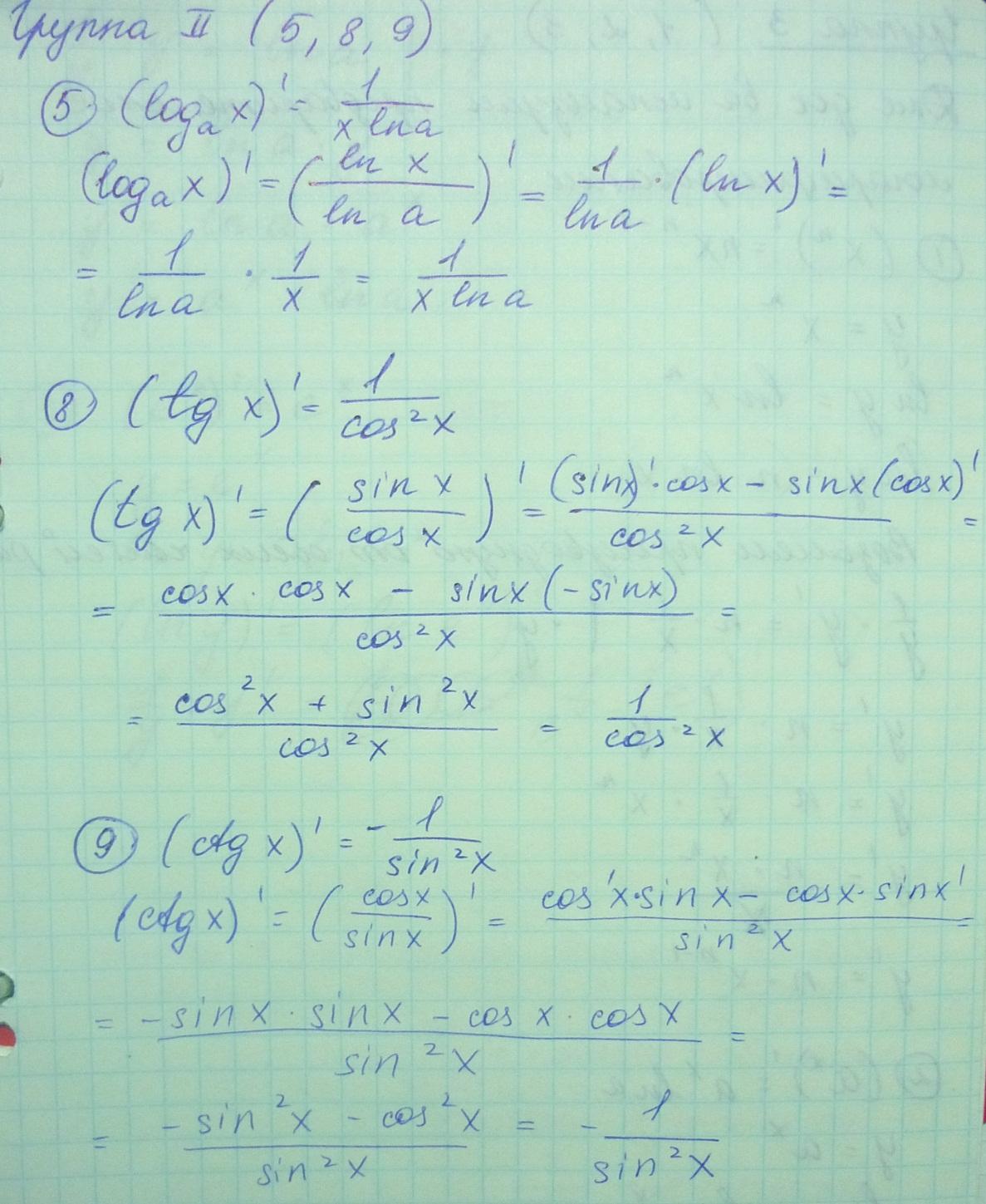
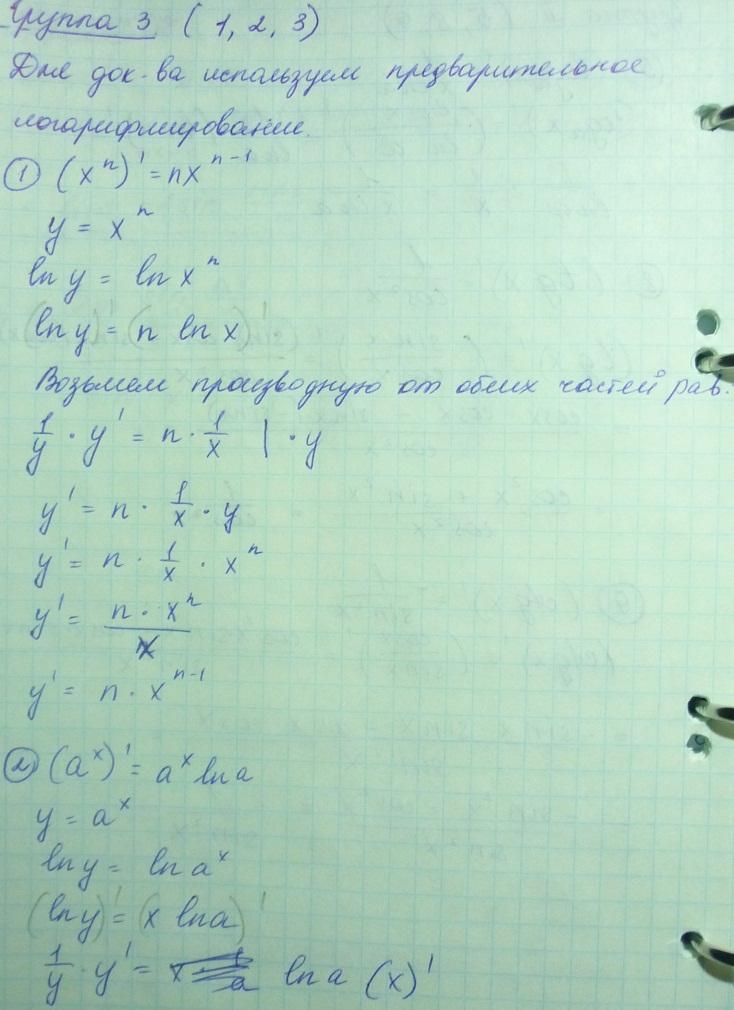
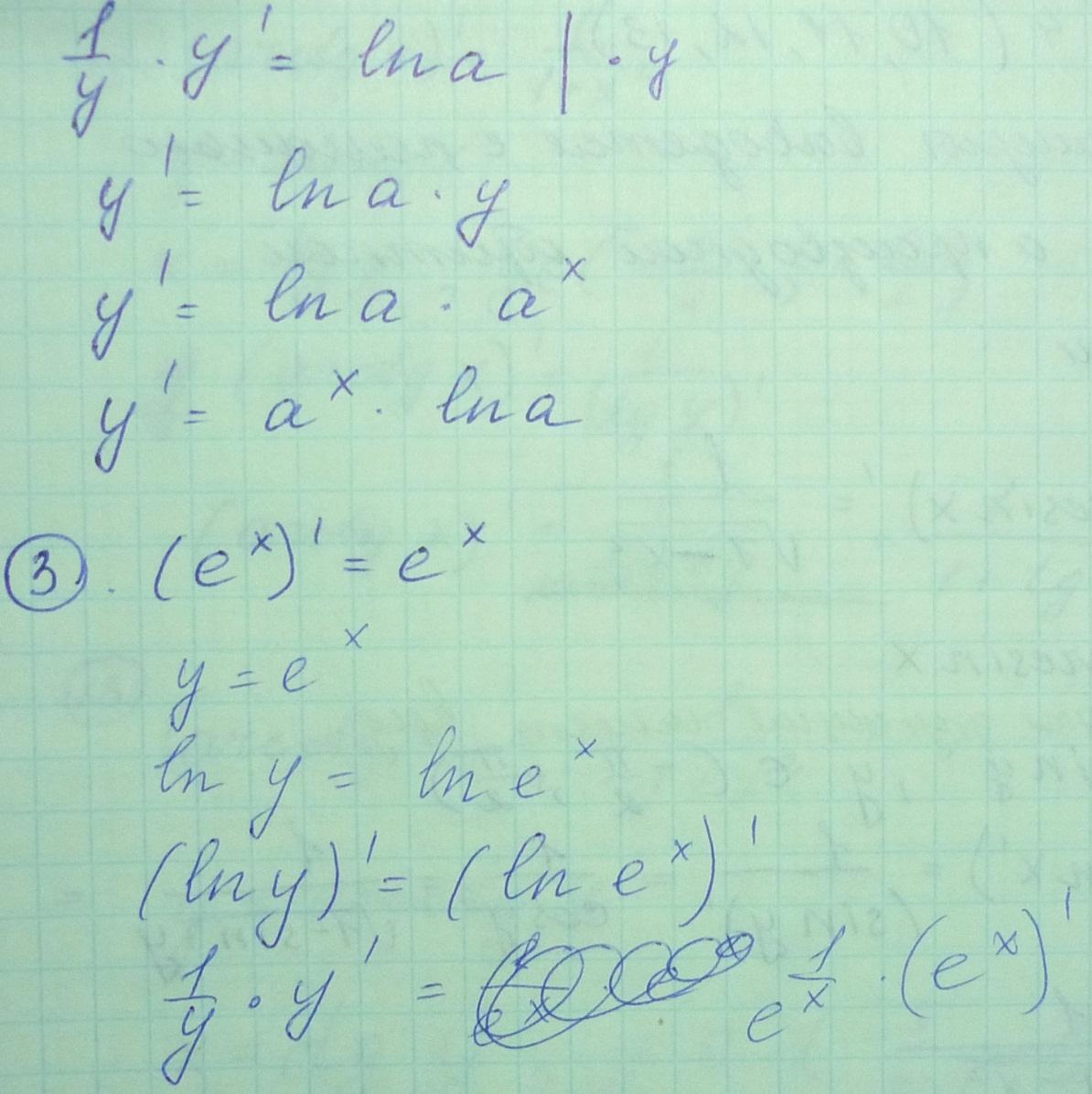

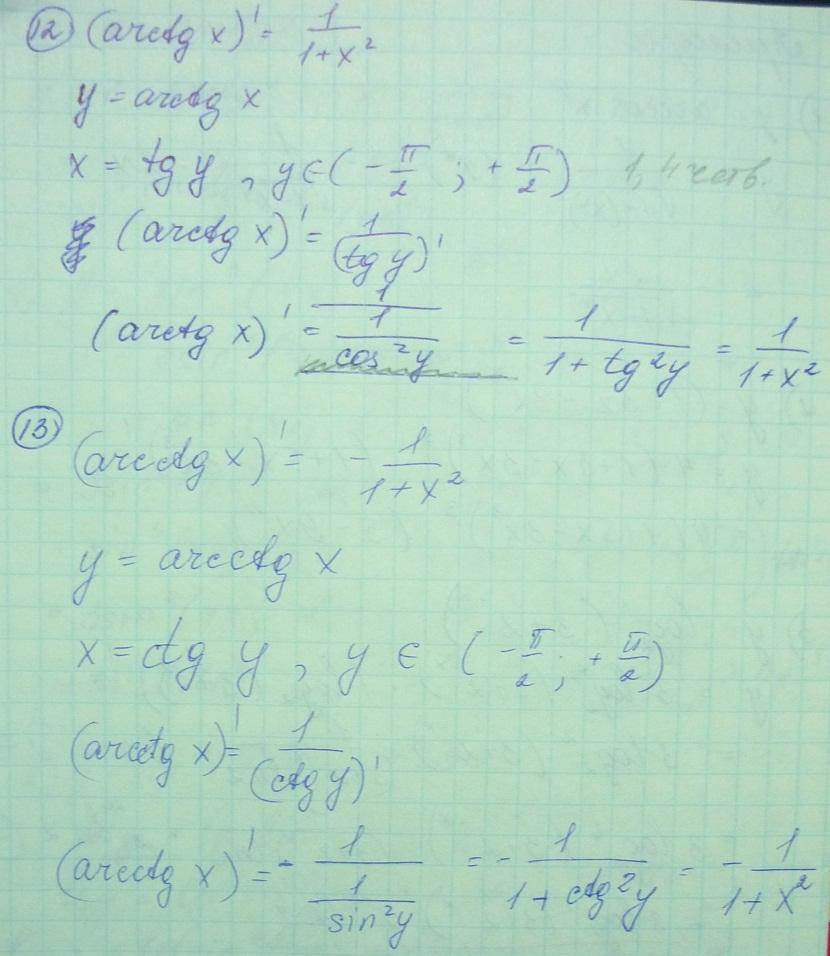
Производные неявно заданной функции.
Под неявным заданием функции понимают задание функции в виде уравнения, не разрешенного относительно y.
F(x;y) = 0.
Для нахождения производной y по x нет необходимости разрешать уравнение относительно y. Достаточно это уравнение продифференцировать по х, рассматривая при этом y как функцию х, и затем полученное уравнение разрешить относительно y’.
Пример:
y + 2x + cosy – 1 = 0
1*y’ + 2*1 – siny*y’ = 0
y’ (1-sin y) = -2
y’
=

Производная параметрически заданной функции.
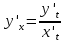
Логарифмическое дифференцирование - метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него.
Пусть дана функция y = f(x).
![]()
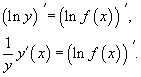
![]()
Производные высших порядков.
Производной второго порядка называется производная от её производной. y’’ = (y’)’
Производного n-го порядка от функции y=f(x) называется производная от производной порядка (n-1)
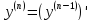
Если
функция задана параметрически, то
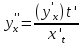 .
.
Теорема Ролля, её геометрический смысл.
Если функция f(x)
-
Непрерывна на
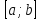
-
Имеет производную на интервале (a;b)
-
На концах
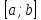 принимает одинаковое значение,
принимает одинаковое значение,
то найдётся хотя бы одна точка С из этого интервала, в которой производная f’(x) обращается в 0, то есть f’(C) = 0.
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Теорема Коши.
Если функция f(x) и g(x)
-
Непрерывна на отрезке
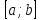
-
Имеет производную на интервале (a;b), причем g’(x) ≠ 0 для любых x ε (a;b),
То найдётся хотя бы одна точка C ε (a;b) такая, что выполняется равенство:

Теорема Лагранжа.
Если функция f(x)
-
Непрерывна на отрезке
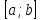
-
Имеет производную на интервале (a;b),
То найдётся хотя бы одна точка C ε (a;b) такая, что выполняется равенство
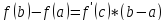 – приращений
функции на
– приращений
функции на
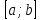 равно приращению аргумента, умноженного
на производную некоторой внутренней
точки этого отрезка.
равно приращению аргумента, умноженного
на производную некоторой внутренней
точки этого отрезка.
Правило Лопиталя.
Рассмотрим
2 функции f(x)
и g(x)
– бесконечно малые (или бесконечно
большие) в точке
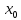 .
.
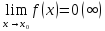
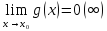
Если
существует предел в точке
 ,
то существует предел отношений производных
(
,
то существует предел отношений производных
(
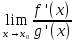 ),
то
),
то
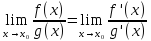
Замечание:
Правило
Лопиталя применяется для раскрытия
неопределённости
 как основных.
как основных.
Экстремум функции.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Точки минимума и максимума функции.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0.
Необходимое условие экстремума (теорема Ферма).
если
функция f(x) имеет
локальный экстремум в точке
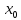 ,
то либо
1)
,
то либо
1) 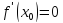 ,
либо
2)
производная
,
либо
2)
производная 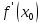 не
существует.
не
существует.
Критические точки.
Точка
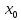 называется критической
точкой функции
f(x) ,
если f(x) непрерывна
в этой точке и либо
называется критической
точкой функции
f(x) ,
если f(x) непрерывна
в этой точке и либо 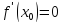 ,
либо
,
либо
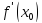 не
существует. В первом случае (то есть
при
не
существует. В первом случае (то есть
при 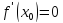 )
точка
)
точка
 называется
также стационарной
точкой функции f(x).
называется
также стационарной
точкой функции f(x).
Достаточные условия экстремума.
Если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума.
Монотонные функции.
Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Критерий монотонности функции.
Пусть
функция ![]() непрерывна
на
непрерывна
на ![]() и
имеет в каждой точке
и
имеет в каждой точке ![]() производную
производную
![]() Тогда:
Тогда:
![]() не
убывает на
не
убывает на ![]() тогда
и только тогда, когда
для любого x
ε (a;b)
f’(x)
≥ 0.
тогда
и только тогда, когда
для любого x
ε (a;b)
f’(x)
≥ 0.
F
не возрастает на ![]() тогда
и только тогда, когда
для любого x
ε (a;b)
f’(x)
≤ 0
тогда
и только тогда, когда
для любого x
ε (a;b)
f’(x)
≤ 0
Выпуклость и вогнутость графика функции.
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Точки перегиба.
Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует
Достаточное условие выпуклости (вогнутости).
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0
для любого x ![]() ( a, b ), то функция f ( x )
является вогнутой на интервале
( a, b );
( a, b ), то функция f ( x )
является вогнутой на интервале
( a, b );
если f '' ( x ) < 0
для любого x ![]() ( a, b ), то функция f ( x )
является выпуклой на интервале
( a, b ) .
( a, b ), то функция f ( x )
является выпуклой на интервале
( a, b ) .
Необходимое условие точки перегиба:
если
функция f(x), дважды дифференцируемая в
некоторой окрестности точки ![]() ,
имеет в
,
имеет в ![]() точку
перегиба, то
точку
перегиба, то ![]() .
.
Достаточное условие точки перегиба:
Если вторая производная дважды дифференцируемой функции при переходе через точку x0, в которой f''(x0) = 0 меняет свой знак, то x0 есть точка перегиба ее графика.
Асимптоты: определение, виды асимптот.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Наклонной
асимптотой графика
функции 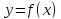 при
при  или
(
или
(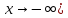 называется
прямая
называется
прямая 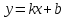 ,
если выполнены два условия:
1)
некоторый луч
,
если выполнены два условия:
1)
некоторый луч 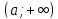 или
или
 целиком
содержится в D(f);
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
целиком
содержится в D(f);
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при 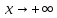 или
или
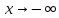 .
.
Формулы для нахождения уравнение асимптоты.
Общая схема исследования функции.
-
Найти ОДЗ и точки разрыва функции.
-
Найти точки пересечения графика функции с осями координат.
-
Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
-
Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
-
Найти асимптоты графика функции: а) вертикальные, b) наклонные.
-
На основании проведенного исследования построить график функции.
