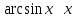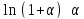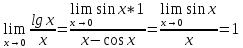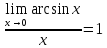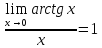- •Определители: определение, вычисление определителей 2-го и 3-го порядка. Решение слау методом Крамера.
- •Прямая на плоскости. Уравнения (вывод)
- •Плоскость. Уравнение (вывод).
- •Прямая в пространстве, уравнения (вывод).
- •Общее уравнение прямой
- •Кривые второго порядка.
- •Числовые последовательности: определение.
- •Непрерывность функции в точке. Точки разрыва, их виды, примеры. Свойства функции, непрерывной на отрезке.
- •Называется точкой разрыва первого рода:
- •Называется точкой разрыва второго рода:
- •Определение производной, её геометрический и физический смысл.
-
Кривые второго порядка.
Уравнение
второй степени относительно двух
переменных
![]() при
разных значениях переменных описывает
4 вида линий на плоскости: окружность,
эллипс, гипербола, парабола.
при
разных значениях переменных описывает
4 вида линий на плоскости: окружность,
эллипс, гипербола, парабола.
-
Окружность – множество точек плоскости, равноудаленных от данной точки.
Уравнение
окружности c
центром (х0; у0) и радиусом R
-
![]()
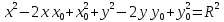
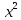 +
+
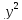 +
(
+
(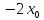 )*x
+ ( -
)*x
+ ( -
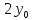 )*y + (
)*y + (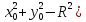 = 0
= 0
-
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой же плоскости (называемых фокусами) есть величина постоянная, большая, чем расстояние между фокусами. F1 (-c;0) F2(c;0)
![]()
F1F2 = 2C
2a > 2C
a > C


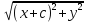 +
+
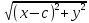 = 2a
= 2a
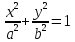 – каноническое
уравнение эллипса
– каноническое
уравнение эллипса
а – большая полуось
b – меньшая полуось
Форма эллипса зависит от величины эксцентриситета.
Эксцентриситет
эллипса может быть выражен через
отношение большой (![]() )
и малой (
)
и малой (![]() )
полуосей:
)
полуосей:
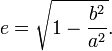
е = с/а, если а>b
e = c/b, если b>a
-
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек (называемых фокусами) есть величина постоянная, меньшая, чем расстояние между фокусами.
![]()
2a < 2c
a < c
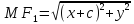
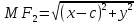
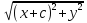 +
+
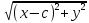 = ± 2a
= ± 2a
-
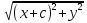 +
+
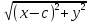 = 2a
= 2a -
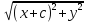 +
+
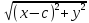 = - 2a
= - 2a
Рассмотрим уравнения в отдельности.
-
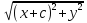 +
+
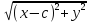 = 2a
= 2a
(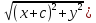 = (2a
+
= (2a
+

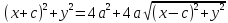 +
+
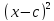 +
+
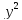
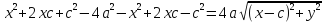
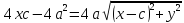 :4
:4
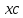 −
−
 ↑2
↑2
 +
+
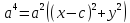
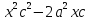 +
+
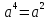 (
(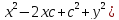
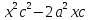 +
+
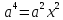 - 2
- 2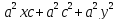
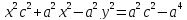
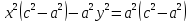 :
:
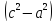 =
=
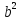
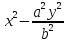 =
=
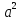 :
:
![]() ,
- каноническое уравнение гиперболы с
центром (о;о), действительной полуосью
а и мнимой полуосью b.
,
- каноническое уравнение гиперболы с
центром (о;о), действительной полуосью
а и мнимой полуосью b.
y
= ±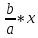 – уравнение асимптот
– уравнение асимптот
е(эксцентриситет) гиперьболы:
е = с/а, а – действительная полуось
e = c/b, b – мнимая полуось
-
Парабола – множество точек плоскости, одинаково удаленных от данной точки (называемой фокусом) и данной прямой (называемой директрисой). Расстояние от фокуса до директрисы называется параметром параболы (p>0).
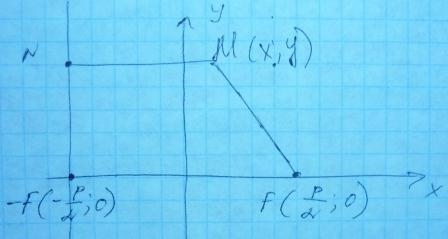
MN = MF
MN
=
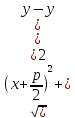
MF
=
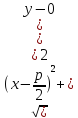
 =
=
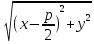
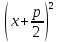 =
=

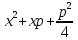 =
=
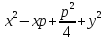
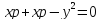
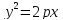 – каноническое
уравнение параболы, симметричной
относительно Ox
с вершиной в точке (0;0) и директрисой x
=
– каноническое
уравнение параболы, симметричной
относительно Ox
с вершиной в точке (0;0) и директрисой x
=
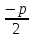
-
Числовые последовательности: определение.
Если
по некоторому закону каждому натуральному
числу n
поставлено в соответствие некоторое
число
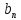 ,
то говорят, что задана числовая
последовательность
,
то говорят, что задана числовая
последовательность
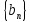
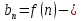 последовательность
можно рассматривать как функцию
натурального аргумента.
последовательность
можно рассматривать как функцию
натурального аргумента.
Определение
предела числовой последовательности:
число a
называется пределом числовой
последовательности
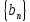 ,
если для любого положительного числа
ε найдётся
такое натуральное число N,
что при n
> N
выполняется неравенство |
,
если для любого положительного числа
ε найдётся
такое натуральное число N,
что при n
> N
выполняется неравенство |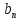 -
a|
< ε.
-
a|
< ε.
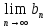 = a
= a
Теорема Вейерштрасса.
Всякая, монотонно возрастающая и ограниченная сверху числовая последовательность имеет предел.
Предел функции в бесконечности.
Число
А называется пределом функции y=f(x)
при x->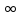 ,
если для любого положительного числа
ε существует
такое положительное число М, что для
всех |x|>M
выполняется равенство
,
если для любого положительного числа
ε существует
такое положительное число М, что для
всех |x|>M
выполняется равенство
|f(x) – A| < ε
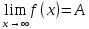
f(x)->
A
при x->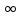
Предел функции в точке.
Пусть
функция y=f(x)
задана в некоторой окрестности точки
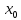 .
.
Число
А называется пределом функции y=f(x)
при
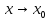 ,
если для любого ε
> 0 найдётся
такое положительное число
,
если для любого ε
> 0 найдётся
такое положительное число
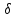 ,
что для всех
,
что для всех
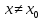 и удовлетворяющих условию |
и удовлетворяющих условию |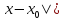 <
<
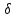 выполняется
неравенство |
выполняется
неравенство |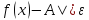 .
.
Односторонние пределы.
Если
при
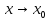 переменная x
принимает только значения
переменная x
принимает только значения
 или только значение
или только значение
 и при этом функция f(x)
-> A,
то говорят об односторонних пределах
функции.
и при этом функция f(x)
-> A,
то говорят об односторонних пределах
функции.
Операции над пределами функции.
-
Lim ( f(x)
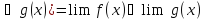
-
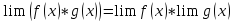
-
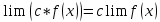
-

-
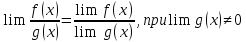
Теорема о пределе промежуточной функции.
Если функция ƒ(х) заключена между двумя функциями φ(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу.
Бесконечно малые и бесконечно большие функции.
Функция
 называется бесконечно малой, если её
называется бесконечно малой, если её
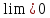
Функция
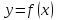 называется бесконечно большой, если её
называется бесконечно большой, если её
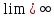
Раскрытие неопределённостей. Примеры.
-
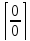 – разложить на
множители числитель и знаменатель
дроби. В результате сократятся множители,
дающие 0.
– разложить на
множители числитель и знаменатель
дроби. В результате сократятся множители,
дающие 0. -
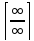 - и
числитель, и знаменатель делим на x
в наибольшей степени из присутствующих.
- и
числитель, и знаменатель делим на x
в наибольшей степени из присутствующих.
-
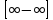 - выражение
представить в виде дроби
- выражение
представить в виде дроби
Первый замечательный предел.
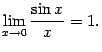
Следствия первого замечательного предела.
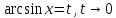
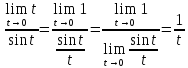 =1
=1
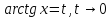
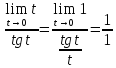 =1
=1
Второй
замечательный предел.
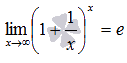 или
в другой записи
или
в другой записи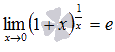
Следствия второго замечательного предела.
-
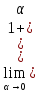 =
e
=
e -
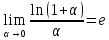
-

Сравнение бесконечно малых.
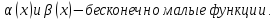
Если
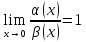 ,
то функция
,
то функция
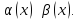
Sin
x