
- •Определители: определение, вычисление определителей 2-го и 3-го порядка. Решение слау методом Крамера.
- •Прямая на плоскости. Уравнения (вывод)
- •Плоскость. Уравнение (вывод).
- •Прямая в пространстве, уравнения (вывод).
- •Общее уравнение прямой
- •Кривые второго порядка.
- •Числовые последовательности: определение.
- •Непрерывность функции в точке. Точки разрыва, их виды, примеры. Свойства функции, непрерывной на отрезке.
- •Называется точкой разрыва первого рода:
- •Называется точкой разрыва второго рода:
- •Определение производной, её геометрический и физический смысл.
-
Прямая на плоскости. Уравнения (вывод)
На плоскости любая прямая определяется уравнением первой степени относительно переменных xи y, и обратно, каждое линейное уравнение вида Ax+By+C = 0 выражает прямую линию.
Рассмотрим задачу:
Составить
уравнение прямой, проходящей через
данную точку
 (
( ;
; ),
принадлежащей прямой L
),
принадлежащей прямой L
А) перпендикулярно n (A;B)
Б) параллельно a (m,n)
Решение:
А)
На искомой прямой L
выберем произвольную текущую точку
М(х,у). Рассмотрим вектор
 М.
М.
 М
(х-
М
(х- ;
у-
;
у- ).
).
Так
как
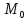 М
перпендикулярно n
==>
М
перпендикулярно n
==>
 М*n
= 0
М*n
= 0
(х- )*А
+ (у-
)*А
+ (у- )*В
= 0
)*В
= 0
Ах
- А + Ву - В
+ Ву - В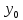 = 0
= 0
Ах+
Ву + ( - А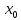 -
В
-
В )
= 0, где - А
)
= 0, где - А -
В
-
В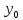 = С
= С
Ах+ Ву +С = 0 – общее уравнение прямой
(А;В) – координаты вектора, ортогонального прямой.
Б)
На искомой прямой L
выберем произвольную текущую точку
М(х,у). Рассмотрим вектор
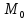 М.
М.
 М
(х-
М
(х- ;
у-
;
у- ).
).
Так
как вектор
 М
II
вектору а, то
М
II
вектору а, то
 =
=
 – каноническое
уравнение прямой, где (
– каноническое
уравнение прямой, где ( координаты
точки, лежащей на прямой.
координаты
точки, лежащей на прямой.
(m;n) – координаты направляющего вектора прямой.
n(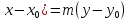
nx
- n – my - m
– my - m = 0
= 0
nx
– my
+ (m - n
- n )
= 0
)
= 0
Где
n
= А, -m
= В, (m - n
- n )
= С
)
= С
Ах+ Ву +С = 0 – общее уравнение прямой
Рассмотрим каноническое уравнение прямой:
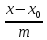 =
=
 = t
= t
 =
t
=
t
 = t
= t
 =tm
x =
=tm
x =
 +tm
+tm
 =tn
y=
=tn
y= +tn
+tn
x
=
 +tm
y=
+tm
y= +tn
- параметрические уравнения прямой,
где t
– любое рациональное число.
+tn
- параметрические уравнения прямой,
где t
– любое рациональное число.
Рассмотрим общее уравнение прямой:
Ах+ Ву +С = 0
Ах+ Ву = -С (: -С)
 x
+
x
+
 y
= 1
y
= 1
 +
+
 = 1, где
a =
= 1, где
a =
 ,
b =
,
b =

 +
+
 = 1 – уравнение прямой в отрезках,
отсекаемых на Ох и Оу.
= 1 – уравнение прямой в отрезках,
отсекаемых на Ох и Оу.
Рассмотрим общее уравнение прямой:
Ах+ Ву +С = 0
Ву = -Ах – С (:В)
У
=
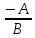 х -
х -

у= kx + b – уравнение прямой с k, равный tg ἀ, где ἀ - угол между прямой и положительным направлением Ох; b – отрезок, отсекаемый на Оу
-
Плоскость. Уравнение (вывод).
Всякая плоскость определяется уравнением первой степени с тремя неизвестными x, y, z и обратно: всякое уравнение вида Ax + By + Cz + D = 0 определяет плоскость.
Рассмотрим плоскость.
Точка М1 (x1; y1; z1) лежит на плоскости. Вектор N (А;В;С) перпендикулярен плоскости.
-
Обозначим на плоскости любую точку М (x;y;z)
-
Обозначим вектор ММ1. Так как вектор ММ1 перпендикулярен вектору N, то ММ1*N = 0.
MM1 (x-x1; y-y1; z-z1)
(x-x1)*A + (y-y1)*B + (z-z1)*C = 0
Ax – Ax1 + By – By1 + Cz – Cz1 = 0
Ax + By + Cz + (-Ax1 – By1 – Cz1) = 0 (-Ax1 – By1 – Cz1) = D
Ax + By + Cz + D = 0 – общее уравнение плоскости
(А; В; С) – координаты нормального вектора плоскости (нормали)
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость.

-
Прямая в пространстве, уравнения (вывод).
-
Общее уравнение прямой
Вектор S (направляющий вектор прямой) = N1 x N2 , где N1 (A1; B1; C1), N2 (A2; B2; C2) (оба вектора перпендикулярны своим плоскостям)
-
Уравнение прямой, проходящей через данную точку М1 (х1, y1, z1) в заданном направлении вектор а = {l, m, n}.
Возьмем
точку М (х, у, z), которая принадлежит
прямой. Вектор ![]() параллелен вектору а, тогда
по условию параллельности векторов их
координаты пропорциональны.
параллелен вектору а, тогда
по условию параллельности векторов их
координаты пропорциональны.
 -
каноническое уравнение прямой в
пространстве.
-
каноническое уравнение прямой в
пространстве.
(l;m;n) – координаты направляющего вектора прямой
(x1; y1; z1) – координаты точки, через которую проходит прямая
-
Рассмотрим каноническое уравнение прямой
 =
t
=
t
 t
; x
= x1
+ lt
t
; x
= x1
+ lt
 ;
y
= y1
+ mt
<<<=====параметрическое
уравнение прямой в пространстве
;
y
= y1
+ mt
<<<=====параметрическое
уравнение прямой в пространстве
 =
t;
z
= z1
+ nt
=
t;
z
= z1
+ nt
(l;m;n) – координаты направляющего вектора прямой
(x1; y1; z1) – координаты точки, через которую проходит прямая
