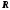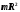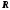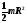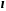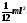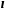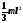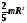- •1. Элементы кинематики Основные формулы и законы
- •2. Динамика материальной точки и поступательного движения твердого тела Основные законы и формулы
- •3. Вращательное движение твердых тел Основные формулы и законы
- •4. Механические колебания Основные формулы
- •Молекулярно-кинетическая теория идеального газа Основные формулы
- •Основное уравнение молекулярно-кинетической теории:
- •6. Основы равновесной термодинамики Основные формулы и законы
- •7. Основы неравновесной термодинамики. Явления переноса Основные формулы и законы
- •Общие методические указания
- •Электростатика Основные формулы и законы
3. Вращательное движение твердых тел Основные формулы и законы
Момент инерции материальной точки
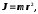
где
 —
масса точки;
—
масса точки; —
расстояние до оси вращения.
—
расстояние до оси вращения.
Момент инерции механической системы (тела) относительно неподвижной оси
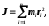
где
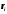 -
расстояние материальной точки массой
-
расстояние материальной точки массой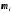 до оси вращения; в случае непрерывного
распределения масс
до оси вращения; в случае непрерывного
распределения масс
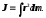
Моменты инерции тел правильной геометрической формы (тела считаются однородными;
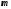 —
масса тела):
—
масса тела):
|
Тело |
Положение оси вращения |
Момент инерции |
|
Обруч
или полый тонкостенный цилиндр
радиусом |
Ось симметрии |
|
|
Сплошной
цилиндр или диск радиусом |
Ось симметрии |
|
|
Прямой
тонкий стержень длиной
|
Ось перпендикулярна стержню и проходит через его середину |
|
|
Прямой
тонкий стержень длиной
|
Ось перпендикулярна стержню и проходит через его конец |
|
|
Шар
радиусом
|
Ось проходит через центр шара |
|
Теорема Штейнера
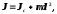
где
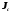 - момент инерции тела относительно оси,
проходящей через центр масс;
- момент инерции тела относительно оси,
проходящей через центр масс; - момент инерции относительно
параллельной оси, отстоящей от первой
на расстоянии
- момент инерции относительно
параллельной оси, отстоящей от первой
на расстоянии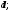
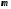 -
масса тела.
-
масса тела.
Момент силы относительно неподвижной точки
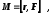
где
 -
радиус-вектор, проведенный из этой точки
в точку приложения силы
-
радиус-вектор, проведенный из этой точки
в точку приложения силы
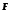 .
Модуль момента силы относительно
неподвижной оси
.
Модуль момента силы относительно
неподвижной оси
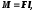
где
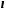 -
плечо силы (кратчайшее расстояние между
линией действия силы и осью вращения).
-
плечо силы (кратчайшее расстояние между
линией действия силы и осью вращения).
Основной закон динамики вращательного движения твердого тела

где
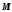 -
момент сил, приложенных к телу;
-
момент сил, приложенных к телу;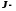 момент
инерции тела относительно оси вращения;
момент
инерции тела относительно оси вращения;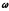 -
угловая скорость тела.
-
угловая скорость тела.
Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси
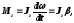
где
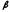 - угловое ускорение;
- угловое ускорение;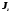 - момент инерции тела относительно осиz.
- момент инерции тела относительно осиz.
Момент импульса (момент количества движения) твердого тела относительно оси вращения
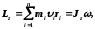
где
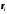 - расстояние от оси
- расстояние от оси до отдельной частицы тела;
до отдельной частицы тела; - импульс этой частицы;
- импульс этой частицы;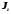 - момент инерции тела относительно
оси
- момент инерции тела относительно
оси ;
; - его угловая скорость.
- его угловая скорость.
Закон сохранения момента импульса для замкнутой системы
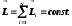
Работа при вращательном движении тела
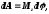
где
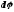 - угол поворота тела;
- угол поворота тела;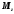 - момент силы относительно оси
- момент силы относительно оси .
.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси

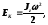
где
 - момент инерции тела относительно оси
- момент инерции тела относительно оси ;
; - его угловая скорость.
- его угловая скорость.
Кинетическая энергия тела, катящегося по плоскости без скольжения,
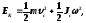
где
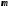 - масса тела;
- масса тела;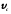 - скорость центра масс тела;
- скорость центра масс тела;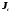 - момент инерции тела относительно оси,
проходящей через его центр масс;
- момент инерции тела относительно оси,
проходящей через его центр масс; - угловая скорость тела.
- угловая скорость тела.
Связь работы и кинетической энергии тела при вращательном движении
 ,
,
где
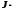 момент
инерции тела относительно оси вращения;
момент
инерции тела относительно оси вращения;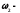 угловая
скорость тела в конечном состоянии;
угловая
скорость тела в конечном состоянии;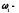 угловая скорость тела в начальном
состоянии.
угловая скорость тела в начальном
состоянии.
4. Механические колебания Основные формулы
Уравнение гармонических колебаний:
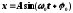 ,
,
где
 –
смещение точки от положения равновесия,А
–
амплитуда колебаний,
–
смещение точки от положения равновесия,А
–
амплитуда колебаний,
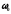 –
круговая (циклическая частота),t
– время,
–
круговая (циклическая частота),t
– время,
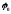 – начальная фаза колебаний.
– начальная фаза колебаний.
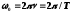 ,
,
где
 –
частота колебаний,
–
частота колебаний,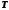 –
период колебаний.
–
период колебаний.
Скорость и ускорение при гармонических колебаниях:
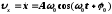 ,
,
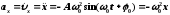 .
.
Возвращающая сила
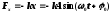 ,
,
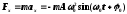 ,
,
где
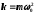 –
коэффициент упругой (квазиупругой)
силы,
–
коэффициент упругой (квазиупругой)
силы,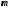 – масса материальной точки.
– масса материальной точки.
Максимальная возвращающая сила
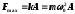
Кинетическая энергия колеблющейся точки
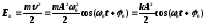
Потенциальная энергия колеблющейся точки
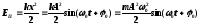
Полная энергия при гармонических колебаниях:
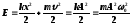 .
.
Периоды колебаний:
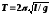 –математический
маятник (
–математический
маятник (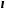 –
длина нити,
–
длина нити,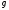 -
ускорение свободного падения),
-
ускорение свободного падения),
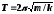 –пружинный
маятник (
–пружинный
маятник ( – масса тела,
– масса тела,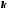 –
жесткость пружины),
–
жесткость пружины),
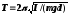 –физический
маятник (
–физический
маятник ( –
момент инерции тела относительно оси,
проходящей через точку подвеса,
–
момент инерции тела относительно оси,
проходящей через точку подвеса,
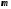 –
масса тела,
–
масса тела,
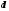 –
расстояние от точки подвеса до центра
масс).
–
расстояние от точки подвеса до центра
масс).
Уравнение затухающих колебаний:
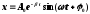 ,
,
где
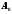 –
амплитуда колебаний в начальный момент
времени,
–
амплитуда колебаний в начальный момент
времени,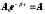 -
амплитуда затухающих колебаний,
-
амплитуда затухающих колебаний,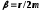 -коэффициент
затухания (
-коэффициент
затухания ( - коэффициент сопротивления,
- коэффициент сопротивления,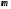 -масса
точки),
-масса
точки), -
частота затухающих колебаний.
-
частота затухающих колебаний.
Логарифмический декремент затухания
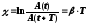 .
.
Амплитуда результирующего колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления:
 ,
,
где
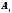 и
и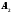 - амплитуды слагаемых колебаний,
- амплитуды слагаемых колебаний,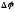 - разность фаз слагаемых колебаний.
- разность фаз слагаемых колебаний.
Начальная фаза результирующего колебания определяется из формулы:

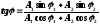 .
.
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами:
 ,
,
где
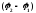 - разность фаз складываемых колебаний.
- разность фаз складываемых колебаний.