4.2. Элементы квантовой механики Основные формулы и законы

• Длина волны де Бройля

,

где – постоянная Планка; – импульс частицы (– масса частицы;– её скорость).

• Связь импульса частицы 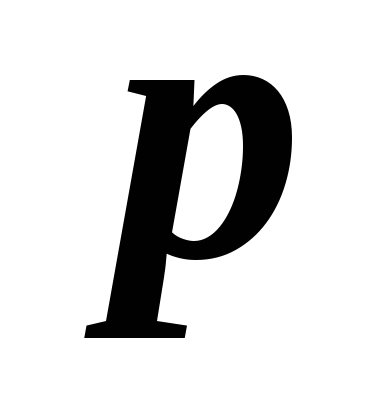с ее кинетической энергией:

,

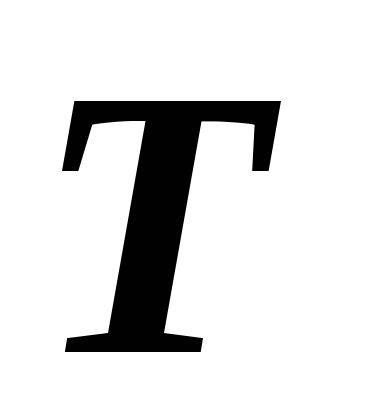где – масса покоя частицы. При малых скоростях .

• Соотношение неопределенностей Гейзенберга

,

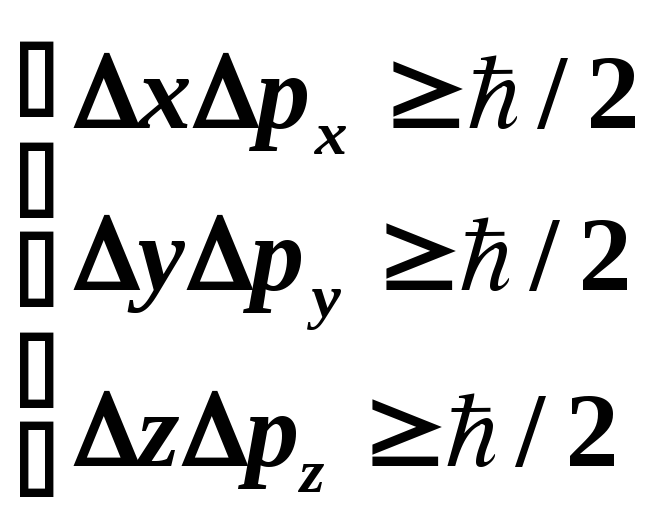
где ,– соответственно неопределенности координаты, импульса, энергии и времени,.

• Нестационарное уравнение Шредингера

.

• Уравнение Шредингера для стационарных состояний

,

где – волновая функция микрочастицы; – полнаяэнергия микрочастицы; =– потенциальная энергия частицы;– пространственная координата (=);t – время, ∆ = – оператор Лапласа (записан в декартовых координатах); – масса микрочастицы; – постоянная Планка; =– мнимая единица.

• Одномерное уравнение Шредингера для стационарных состояний

.

• Условие нормировки волновой функции

.

• Плотность вероятности

,

где – вероятность того, что частица может быть обнаружена вблизи точки с координатой на участке .

• Вероятность обнаружения частицы в интервале от 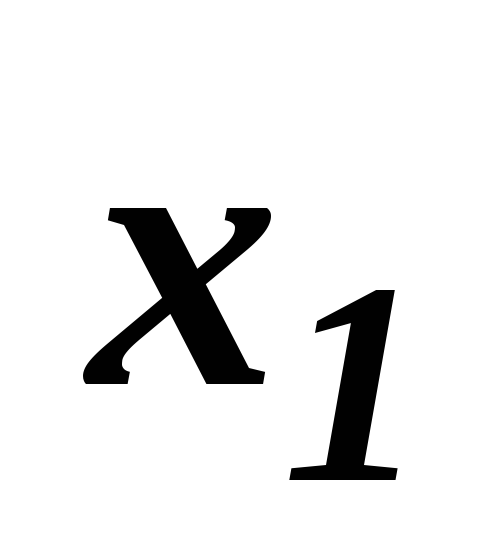до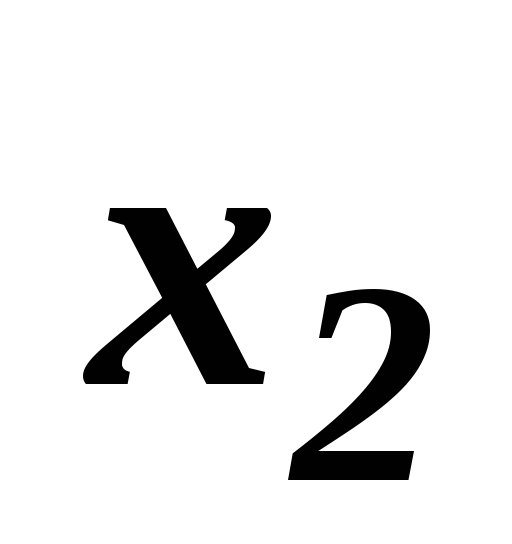

.

• Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной (0 ≥ ≥ )

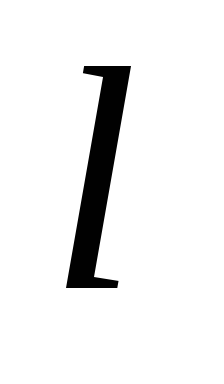(собственная нормированная волновая функция)

(собственное значение энергии),

где – главное квантовое число (= 1, 2, 3,…). В области 0≥≥ = ∞ и= 0.

• Коэффициент прозрачности прямоугольного потенциаль-ного барьера

,

где – постоянный множитель (можно приравнять единице);– высота барьера;– полная энергия частицы;– ширина барьера.

• Энергия квантового осциллятора

,

где – главное квантовое число (=0, 1, 2,…);– собственная частота колебаний осциллятора.

• Для частиц с целочисленными спинами (бозонов) справедлива статистика Бозе-Эйнштейна, а для частиц с полуцелыми спинами (фермионов) справедлива статистика Ферми-Дирака. Обобщенное уравнение для квантовых статистик

,

где - среднее число частиц в состоянии с номеромi, – энергия частицы в этом состоянии;  – так называемый химический потенциал, определяемый из условия , т. е. сумма всех частиц равна полному числу частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми-Дирака).

Задания Волновые свойства микрочастиц

4.16. Вычислить длину волны де Бройля для протона, прошедшего разность потенциалов U = 10 В. [9,1 пм].

4.17. При какой скорости электрона дебройлевская длина волны будет равна: а) 500 нм; б) 0,1 нм? (В случае электромагнитных волн первая длина волны соответствует видимой части спектра, вторая – рентгеновским лучам). [1,46 ∙10³ м/с; 0,73 ∙10⁷ м/с].

4.18. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислить длину волны де Бройля для такого электрона. [86 пм].

4.19. На грань кристалла никеля падает под углом 64^о к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Принимая расстояние между атомными плоскостями кристалла равным 200 пм, определить скорость электронов, если они испытывают дифракционное отражение первого порядка. [2 Мм/с].