
Задание 81
Найдите
длину дуги кривой ![]() между точками
между точками ![]() и
и ![]() :
:
|
|
|
|
|
|
1) |
|
-1,9 |
1,3 |
|
2) |
|
-2,2 |
1,6 |
|
3) |
|
-3 |
1,3 |
|
4) |
|
-3,3 |
2,7 |
|
5) |
|
-2,9 |
3,5 |
|
6) |
|
-3,9 |
1,2 |
|
7) |
|
-3,8 |
3,2 |
|
8) |
|
-4 |
3 |
|
9) |
|
2,5 |
1,4 |
|
10) |
|
-1 |
1,7 |
Задание 82
Найдите длину дуги кривой, заданной указанными уравнениями:
1) x = e-2tcos3t, y = e-2tsin3t, 0 t 6;
2) x = 4(t – sint), y = 4(1 – cost), 0 t 2;
3) x = 3(cost + tsint), y = 3(sint – tcost), 0 t 3;
4) x = e2tsin4t, y = e2tcos4t, 0 t 8;
5) x = (t2 – 2) sint + 2tcost, y = (2 – t2) cost+2tsint, 0 t ;
6) x = 3(1 – sint), y = 3(t – cost), 0 t 2;
7) x = e4tcos2t, y = e4tsin2t, 0 t 6;
8) x = 8cos3t, y = 8sin3t, 0 t 6;
9) x = 3(2cost – cos2t), y = 3(2sint – sin2t), 0 t 2;
10) x = e3tsin2t, y = e3tcos2t, 0 t 4.
Задание 83
Найдите
объем тела, образованного вращением
вокруг оси ![]() фигуры, ограниченной линиями
фигуры, ограниченной линиями ![]() и осью
и осью ![]() (a
(a![]() ):
):
|
№ |
|
|
|
№ |
|
|
|
|
1) |
-0,3x2+1,2x+4 |
-0,9 |
2,8 |
6) |
-0,6x2+1,1x+4 |
0,7 |
2,9 |
|
2) |
-0,3x2+1,4x+3 |
-0,1 |
2,2 |
7) |
0,6x2-0,6x+2 |
-0,2 |
1,4 |
|
3) |
-0,3x2+1,1x+6 |
-0,3 |
1,4 |
8) |
0,4x2-0,5x+4 |
-1 |
1,3 |
|
4) |
-0,5x2+1,2x+3 |
0 |
2 |
9) |
-0,6x2+1,3x+5 |
-0,6 |
1,3 |
|
5) |
-0,3x2+1,8x+5 |
0,1 |
2,6 |
10) |
-0,4x2+1,8x+3 |
-0,5 |
2,9 |
Задание 84
Найдите объём тела, образованного вращением вокруг оси 0x фигуры, ограниченной линией, заданной указанным уравнением:
1)
![]() ,
,![]() ;2)
;2)
![]() ,
,![]() ;
;
3)
![]() ,
,![]() ;4)
;4)
![]() ,
,![]() ;
;
5)
![]() ,
,![]() ;6)
;6)![]() ,
,![]() ;
;
7)
![]() ,
,![]() ;8)
;8)![]() ,
,![]() ;
;
9)
![]() ,
,![]() ;10)
;10)
![]() ,
,![]() .
.
ЗАДАНИЕ 85
Область
(D)
задана указанными неравенствами: 1)
постройте область (![]() );
2) запишите двойной интеграл
);
2) запишите двойной интеграл![]() в виде повторного; 3) измените порядок
интегрирования:
в виде повторного; 3) измените порядок
интегрирования:
1)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
2) а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
3)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
4)
а)
![]() ; в)
; в)![]()
б)
![]() ; г)
; г)![]() ;
;
5)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
6)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
7) а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
8)
а)
![]() ; в)
; в)![]()
б)
![]() ; г)
; г)![]() ;
;
9)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() ;
;
10)
а)
![]() ; в)
; в)![]() ;
;
б)
![]() ; г)
; г)![]() .
.
ЗАДАНИЕ 86
Измените порядок интегрирования:
1)
![]() ; 2)
; 2)![]() ;
;
3)
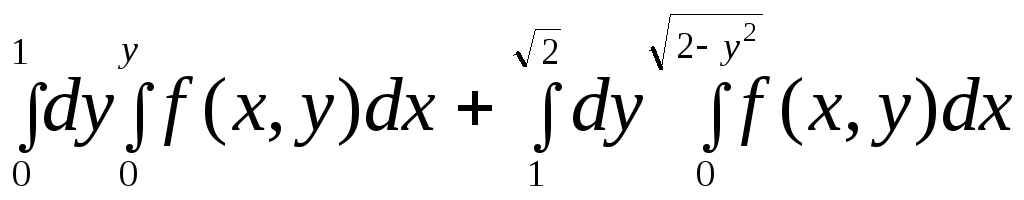 ; 4)
; 4)![]() ;
;
5)
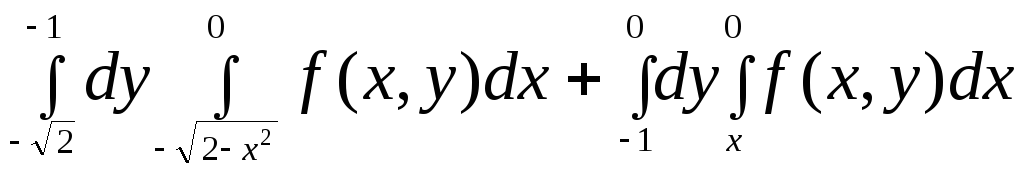 ; 6)
; 6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 87
Вычислите интегралы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)![]() ;
;
10)
![]() .
.
ЗАДАНИЕ 88
В
области
![]() ,
ограниченной заданными линиями,
вычислить двойной интеграл двумя
способами (т.е. изменяя порядок
интегрирования по
,
ограниченной заданными линиями,
вычислить двойной интеграл двумя
способами (т.е. изменяя порядок
интегрирования по![]() и по
и по![]() ).
Сделать рисунок:
).
Сделать рисунок:
1)
![]() ;
;
2)
![]() ;
;
3)![]() ;
;
4)
![]() ;
;
5)![]() ;
;
6)![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
