Глава II. Определенный интеграл

§1. Определение. Формула Ньютона–Лейбница

1. Пусть дана непрерывная на отрезке функция. Разобьемточками,наотрезков длиной(рис. 1) и составим сумму, которая называетсяинтегральной суммой для функции на отрезке.

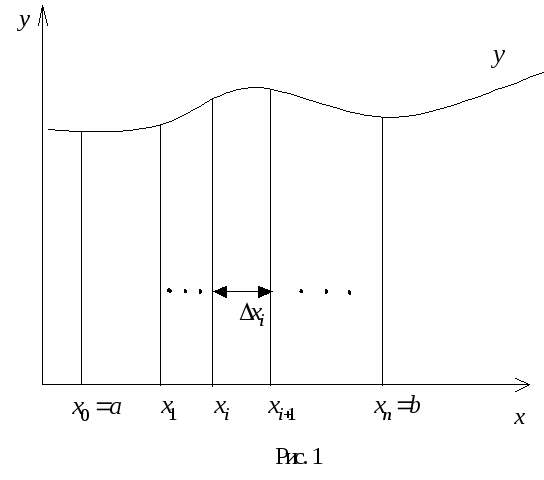
Каждое слагаемое этой суммы приближенно равно площади прямоугольника высотой и с основанием, поэтому вся сумма будет приближенно равна площади криволинейной трапеции, ограниченной прямыми,, отрезкомна осии кривой.

Если функция непрерывна на отрезке, то при всехсуществует предел суммы (13), не зависящий от способа разбиения отрезка. Этот предел называетсяопределенным интегралом от функции на отрезкеи обозначается. Т.о.:

.

Числа иназываютнижним и верхним пределами интегрирования, –подынтегральной функцией, а –переменной интегрирования.

В отличие от неопределенного интеграла, определенный интеграл представляет собой число, а не функцию. Если интеграл существует, то это число определяется однозначно и зависит только от вида функции и от чисели. Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для переменной интегрирования:

и т.д.

Пусть функция является интегрируемой на отрезке функцией. В этом случае будем писать . Здесьобозначает множество всех интегрируемых на функций (вспомните, что представляют из себя множества и).

2. Условия существования определенного интеграла

ТЕОРЕМА (необходимое условие интегрируемости функции)

Если ,то она ограничена на .

Замечание

Обратная теорема неверна, т.е. условие ограниченности функции является необходимым, но не достаточным условием интегрируемости функции.

ТЕОРЕМА (достаточное условие интегрируемости функции)

Если функция ограничена на отрезкеи имеет на нем конечное число точек разрыва, то .

Следствие

Если , то (т.е. имеет место включение .

Пусть функция является интегрируемой на отрезке функцией. В этом случае будем писать . Здесьобозначает множество всех интегрируемых на функций (вспомните, что представляют из себя множества и).

3. Свойства определенного интеграла

Сначала расширим понятие определенного интеграла. В определении мы считали, что . Распространим определение на случаии, полагая

и .

1) если – константа, то;

2) если и, то;

3) если , тодля любого отрезка;

4) аддитивность интеграла. Для любых чисел имеет место равенство

;

5) линейность интеграла. Если и, то для любыхфункция. При этом справедливо равенство

.

В частности (при),

(при );

6) Если идля, то

;

7) Если идля, то

.

8. ТЕОРЕМА (о среднем значении)

Если идля, тотакое, что

.

Данной теореме можно придать другую форму, если учесть включение .

Если , тотакое, что

.

Теорема о среднем имеет простой геометрический смысл: существует точка такая, что площадь криволинейной трапецииравна площади прямоугольника, имеющего высотуи основание(рис. 2).

9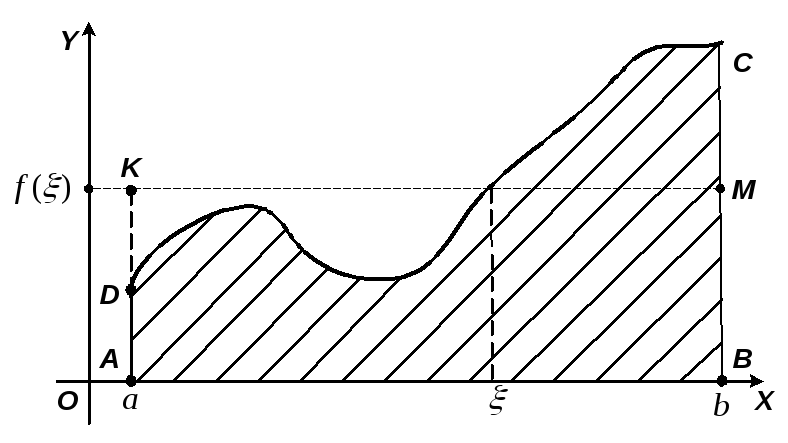. Интеграл с переменным верхним пределом.

Если , то интегрируема по любой части этого отрезка, и поэтому длясуществует интеграл, называемыйинтегралом с переменным верхним пределом.

Значение функции раскрывает следующая теорема.

ТЕОРЕМА

Если , то функциядифференцируема в любой внутренней точкеэтого отрезка (), причем.

Замечание. Любая непрерывная на отрезке функцияимеет на этом отрезке первообразную, а именно, функцию . Поскольку всякая другая первообразная для функции может отличаться оттолько на постоянную, то тем самым установлена связь между неопределенным и определенным интегралами в виде, где– произвольная постоянная.

10. ТЕОРЕМА

Если функция , то

,

где – первообразная для функции.

Данная формула называется формулой Ньютона-Лейбница.

Разность принято условно записывать в виде, поэтому

.