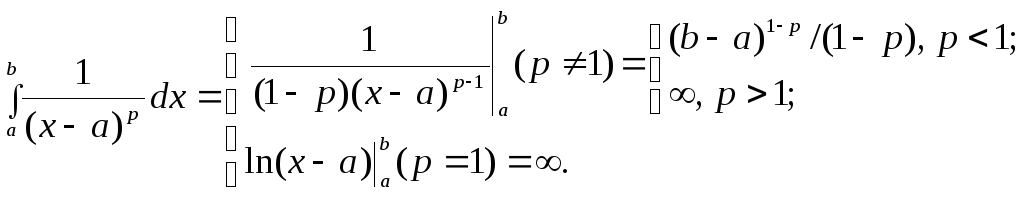- •Глава I. Неопределеннный интеграл
- •§1. Определение. Общие приемы и методы интегрирования
- •2. Свойства неопределенного интеграла
- •3. Таблица основных интегралов
- •4. Методы интегрирования
- •4.1. Непосредственное интегрирование
- •4.3. Интегрирование по частям Пусть две дифференцируемые функции изависят от. Тогда
- •§2. Интегрирование рациональных функций.
- •Интегрирование произвольных рациональных дробей Пусть дан интеграл вида
- •§3. Интегрирование тригонометрических функций
- •§4. Интегрирование иррациональных выражений
- •3. Интегрирование функций вида и
- •Глава II. Определенный интеграл
- •§1. Определение. Формула Ньютона–Лейбница
- •2. Условия существования определенного интеграла
- •3. Свойства определенного интеграла
- •§2. Методы вычисления определенных интегралов
- •1.2. Область задана в полярных координатах
- •2. Вычисление длин кривых
- •2.1. Определение спрямляемой кривой и длины кривой
- •2.2. Длина кривой в декартовых координатах
- •2.4. Кривая задана в полярных координатах
- •3. Объёмы тел вращения
- •3.2. Объём тела, получающегося при вращении кривой вокруг координатной оси
- •4. Площадь поверхности вращения
- •§4. Определенный интеграл в экономике
- •1. Экономический смысл определенного интеграла
- •2. Восстановление функций экономического анализа по их предельным характеристикам
- •3. Определенный интеграл в финансовом анализе
- •Глава III. Несобственные интегралы
- •§1. Интегралы с бесконечными пределами (несобственные интегралы первого рода)
- •2. Признак сравнения
- •3. Признак сравнения в предельной форме
- •§2. Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода).
- •2. Признаки сравнения
- •3. Признак сравнения в предельной форме
- •Главное значение
- •Глава I V. Кратные интегралы
- •§1. Двойной и тройной интегралы, их свойства. Геометрический смысл двойного интеграла
- •2. Свойства двойных интегралов
- •3. Тройной интеграл
- •4. Геометрический смысл двойного интеграла
- •5. Вычисление двойного интеграла в декартовых координатах путем сведения его к повторному
- •Вопросы промежуточного контроля
- •Типовые задания для контроля знаний и закрепления практических навыков
3. Признак сравнения в предельной форме
Пусть
неотрицательные функции f(x)
и g(x)
интегрируемы по любому отрезку [a,
b]
и пусть существует конечный
![]() .
Тогда несобственные интегралы
.
Тогда несобственные интегралы![]() и
и![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Сравнение
интеграла
![]() со "стандартным" интегралом
со "стандартным" интегралом![]() в предельной форме позволяет сформулировать
такое правило: если при
в предельной форме позволяет сформулировать
такое правило: если при![]() неотрицательная функцияf(x)
– бесконечно малая порядка малости
выше первого по сравнению с
неотрицательная функцияf(x)
– бесконечно малая порядка малости
выше первого по сравнению с
![]() ,
то
,
то![]() сходится; еслиf(x)
не является бесконечно малой или имеет
порядок малости единица или ниже, то
интеграл расходится.
сходится; еслиf(x)
не является бесконечно малой или имеет
порядок малости единица или ниже, то
интеграл расходится.
Типовые примеры
1.
![]() .
.
►При
![]()
![]() эквивалентна функции
эквивалентна функции![]() ,
поэтому интеграл сходится. ◄
,
поэтому интеграл сходится. ◄
2.
![]() .
.
►При
![]()
![]() эквивалентна функции
эквивалентна функции![]() ,
поэтому интеграл расходится. ◄
,
поэтому интеграл расходится. ◄
3.
![]() .
.
►При
![]()
![]() эквивалентна функции
эквивалентна функции![]() ,
поэтому интеграл расходится. ◄
,
поэтому интеграл расходится. ◄
4.
![]() .
.
►При
![]()
![]() эквивалентна функции
эквивалентна функции![]() ,
поэтому интеграл расходится. ◄
,
поэтому интеграл расходится. ◄
Типовые примеры
Исследовать интегралы на абсолютную сходимость:
1.
![]() .
.
►![]() ;
интеграл от большей функции сходится,
следовательно,
;
интеграл от большей функции сходится,
следовательно,
![]() сходится, следовательно, исходный
интеграл сходится абсолютно. ◄
сходится, следовательно, исходный
интеграл сходится абсолютно. ◄
2.
![]() .
.
►![]() ,
первый множитель,
,
первый множитель,
![]() ,
стремится к нулю при
,
стремится к нулю при![]() ,
следовательно, ограничен:
,
следовательно, ограничен:![]() ,
интеграл от последней функции сходится,
следовательно, исходный интеграл
сходится абсолютно. ◄
,
интеграл от последней функции сходится,
следовательно, исходный интеграл
сходится абсолютно. ◄
Приведённые
примеры показывают, что переход от
![]() к
к![]() и применение к последнему интегралу
методов исследования на сходимость
несобственных интегралов от неотрицательных
функций, в случае его сходимости,
позволяет сделать вывод и о сходимости
(притом, абсолютной) исходного интеграла.
Если же интеграл от |f(x)|
расходится, решение задач значительно
усложняется.
и применение к последнему интегралу
методов исследования на сходимость
несобственных интегралов от неотрицательных
функций, в случае его сходимости,
позволяет сделать вывод и о сходимости
(притом, абсолютной) исходного интеграла.
Если же интеграл от |f(x)|
расходится, решение задач значительно
усложняется.
§2. Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода).
1.
Пусть функция
![]() не определена в точке
не определена в точке![]() .
Тогда интеграл от нее на отрезке
.
Тогда интеграл от нее на отрезке![]() будет несобственным и вычисляется по
формуле
будет несобственным и вычисляется по
формуле
![]() .
.
Аналогично
определяется несобственный интеграл,
если функция
![]() не определена на нижнем пределе.
не определена на нижнем пределе.
Типовые примеры
1.
![]() .
.
►![]() –интеграл
расходится; ◄
–интеграл
расходится; ◄
2.
![]() .
►
.
►![]()
![]() –интеграл
сходится. ◄
–интеграл
сходится. ◄
3.
![]() .
.
►
![]() –интеграл
сходится.◄
–интеграл
сходится.◄
Если
функция
![]() не определена или имеет разрыв 2-го рода
в некоторой точке
не определена или имеет разрыв 2-го рода
в некоторой точке![]() внутри отрезка
внутри отрезка![]() (или внутри интервалов
(или внутри интервалов![]() ,
,![]() ),
то интеграл также будет несобственным
и определяется равенством:
),
то интеграл также будет несобственным
и определяется равенством:
![]() =
=![]() +
+![]() =
=![]() .
.
Типовой пример
![]() .
.
►![]()
![]()
![]() ,
и интеграл расходится, так как все три
предела бесконечны. ◄
,
и интеграл расходится, так как все три
предела бесконечны. ◄
2. Признаки сравнения
Как и для несобственных интегралов первого рода, для интегралов второго рода вводится понятие абсолютной сходимости, позволяющее в ряде случаев свести исследование сходимости интегралов от произвольных функций к исследованию сходимости интегралов от неотрицательных функции, и рассматриваются признаки сравнения для таких интегралов. Будем предполагать, что подынтегральная функция имеет особенность на левом конце промежутка интегрирования.
Признак сравнения
Пусть
функции
![]() и
и![]() интегрируемы по любому отрезку
интегрируемы по любому отрезку![]() и при
и при![]() удовлетворяют неравенствам
удовлетворяют неравенствам![]() .
Тогда:
.
Тогда:
если
сходится интеграл
![]() ,
то сходится интеграл
,
то сходится интеграл![]() ;
;
если
расходится интеграл
![]() ,
то расходится интеграл
,
то расходится интеграл![]() .
.
В
качестве "стандартного" интеграла,
с которым сравнивается данный, и в этом
случае обычно берётся интеграл от
степенной функции типа
![]() .
Этот интеграл сходится, еслиp
< 1, и расходится, если
.
Этот интеграл сходится, еслиp
< 1, и расходится, если
![]() :
: