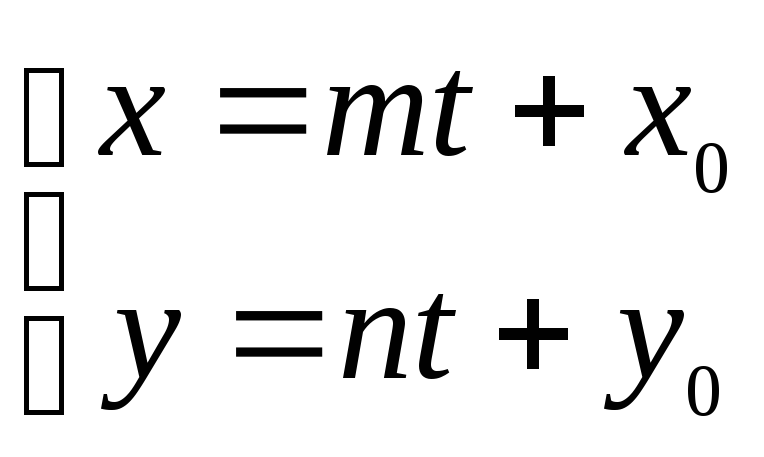6. Параметрическое уравнение

Пусть в каноническом уравнении , где– параметр,.

Тогда

(8) – параметрические уравнения прямой

Придавая в (8) параметру конкретные значения, мы будем получать координаты точек, лежащих на прямой.

7. Уравнение прямой с угловым коэффициентом

Положение всякой прямой однозначно определяется любой точкой , лежащей на этой прямой и углом , который образует эта прямая с положительным направлением оси. Тангенс угла(часто говорят: «угол наклона прямой к оси») называютугловым коэффициентом прямой. Обозначим .

Заметим, что для прямой, параллельной оси, угловой коэффициентравен нулю, а для прямой, перпендикулярной оси, угловой коэффициент не существует (в последнем случае иногда формально говорят, что угловой коэффициент «обращается в бесконечность»).

Пусть – общее уравнение прямой на плоскости. Предположим, что . Тогда  , где,.

Исследуем геометрический смысл коэффициента .

Пусть и . Поскольку точки и принадлежат прямой , их координаты удовлетворяют ее уравнению:

,

.

Вычитая первое уравнение из второго, имеем:

, где ,.

Таким образом, –уравнение прямой (9)

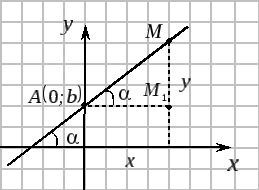
на плоскости с угловым коэффициентом .Здесь — угол, который прямая образует с осью ,— точка, в которой прямая пересекает ось(),— координаты текущих точек прямой . Если прямая проходит через точку и известен угловой коэффициент, то

(10) – уравнение прямой, проходящей через данную точку в данном направлении

Типовой пример. Пусть прямая задана общим уравнением: . Требуется написать ее уравнение с угловым коэффициентом.

►Имеем: =. Следовательно, угловой коэффициентравен. Очевидно,– координаты точки, в которой прямая пересекает ось,— координаты точки, в которой прямая пересекает ось.◄

Пример. Функция спроса является линейной убывающей функцией. Ее графиком является прямая, которая проходит через точкиA(0,100) и B (50,0).

Пример. Функция полных издержек некоторой фирмы задана уравнением (тыс. руб.), где- объем производства (число единиц продукции). При этом цена производимой продукции на рынке равнатыс. руб. за ед. продукции. При каких значениях объема производства прибыль фирмы положительна?

►В данном случае прибыль фирмы определяется как сумма доходов (выручка от продажи) минус полные издержки производства. Поэтому

откуда следует условие безубыточности , приводящее к решению. Итак, приприбыль отрицательна (в этом случае издержки производства превосходят выручку от продажи), а приприбыль положительна (в этом случае выручка от продажи превосходит издержки производства). Значениеназываютточкой безубыточности. ◄

Пример. Спрос на некоторый товар при цене 100 руб. за 1 ед. равен 1500 ед., а при цене 150 руб. за 1 ед. – 1200 ед. Предполагая, что спрос линейно зависит от цены, вывести уравнение функции спроса и определить спрос при цене 120 руб. за 1 ед.

►Для линейной функции спроса, которую удобно записать в виде , где , при P₁ =100, Q₁ =1500, P₂ =150, Q₂ =1200 получаем Q=1500- 6 (P-100), и, таким образом, функция спроса имеет вид Q=2100-6 P. Из этого уравнения легко вычислить значение функции спроса при цене P=120: Q(120)=2100-6·120=2100 – 720 =1380 (ед.). ◄

Прямая разделяет плоскость на две полуплоскости. В первой из этих полуплоскостей координаты любой точки удовлетворяют неравенству

а во второй – неравенству

.

Линейные неравенства данного вида используются для формализованного описания различных ограничений (ресурсных, бюджетных и пр.) в простейших задачах экономического анализа.

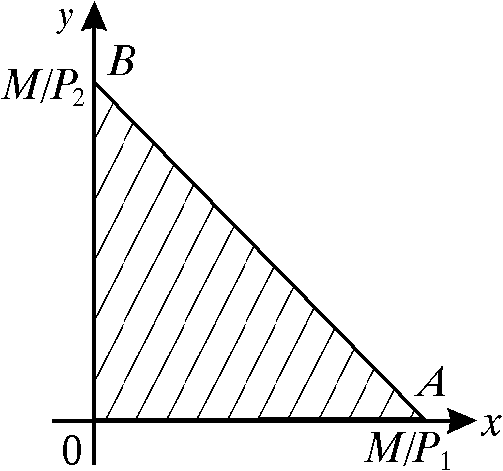
Пример. Построить бюджетное множество, которое отражает покупательные возможности потребителя двух товаров, если на приобретение этих товаров можно израсходовать не более 10000 руб. Известно, что цены товаров равны 250 руб. и 500 руб. соответственно.

►Если покупатель приобретает первый товар в количестве единиц, а второй – в количествеединиц, то в силу условия задачи получаем:

,

где руб./ед.,руб./ед.,руб.

Равенство задает на плоскостипрямую, которая отсекает на координатных осях отрезки длинойи. Эта прямая называется – бюджетной линией. Данные неравенства определяют треугольник , точки которого и задают бюджетное множество. Точки иимеют координаты) и соответственно. Верхняя граница бюджетного множества – бюджетная линия .◄