§4. Непрерывность функции

1. Непрерывность функции в точке

Пусть функция определена в точкеи в некоторой окрестности точки.

Функция называетсянепрерывной в точке , если предел её в этой точке равен значению функции в этой точке, т.е. если

= . (1)

Следствие. Если функция непрерывна в точке , то к пределу можно перейти под знаком функции, т.е.

= . (2)

Функция называетсянепрерывной в точке , если выполняется условие.

Разность – =называютприращением аргумента, а разность – = – = –приращением функции в точке = .

Функция называетсянепрерывной в точке , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, т.е. .

Типовой пример

Доказать, что функция непрерывна в точке.

►1) По второму определению: .

2) Доказательство на языке приращений

. ◄

Типовой пример

Доказать, что функция непрерывна в точкех₀=3.

►П

риведем два доказательства.Доказательство на языке . Рассмотрим- окрестность точки. Дляимеем:или. Далее дляимеем:

Для числителя имеем: . Для знаменателя имеем:x-3 достаточно мало и поэтому 4+x-3>0. Тогда , так как. Следовательно,. Пусть. Тогда. Итак, дляможно подобратьтакое, чтодля всехх: . Очевидно, чтоможно выбирать и меньше полученного числа, т.е..

Доказательство на языке приращений. Имеем: .

Так как , то функция непрерывна в точкех₀=3. Преимущество второго метода доказательства несомненно. ◄

2. Точки разрыва функции

Если требования непрерывности функции в точке не выполняются, т.е. функция не определена в точкеили предел функции в точкене существует, или существует, но не равен значению функции в этой точке, то функция называетсяразрывной в точке , а сама точканазываетсяточкой разрыва функции.

Если функция имеет предел в точке , но он не совпадает со значением функции в этой точке или функция не определена в этой точке, то разрыв называетсяустранимым.

Если функция имеет в точке односторонние пределы, не равные между собой, тоназываетсяточкой разрыва первого рода. При этом –= называетсяскачком функции в точке .

Если хотя бы один из односторонних пределов не существует или бесконечный в точке , то этаточка разрыва второго рода.

Итак, функция терпитразрыв в точке в одном из следующих случаев:

1), но, либоне определено (рис.1); в этом случае говорят, что– точкаустранимого разрыва;

2) – конечные, но не равные между собой пределы; такая точка называетсяточкой разрыва первого рода (говорят, чтотерпит в точкескачок) (рис.2);

3) по крайней мере одного из односторонних пределов в точкене существует (т.е. не существует конечного предела); в таком случае говорят, чтоx₀ – точка разрыва второго рода (рис.3).

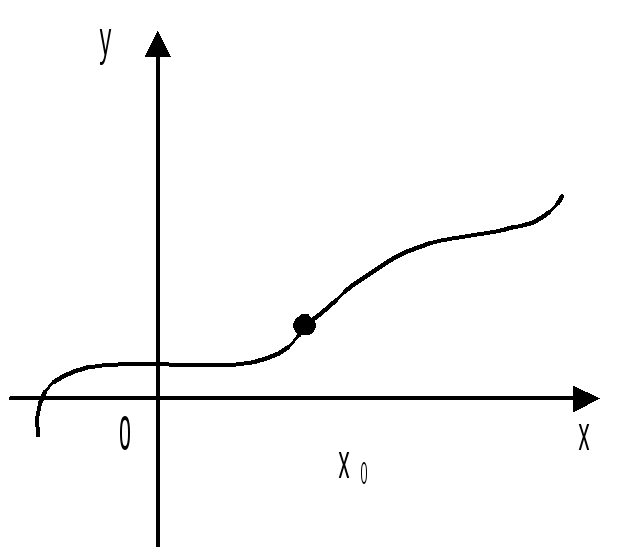
Рис.1	Рис.2
Рис. 3

Если функция непрерывна в каждой точке интервала (,), то она называетсянепрерывной на этом интервале. Если = , то функция называется непрерывной в точке слева. Аналогично при = – непрерывной в точке справа.

Если функция непрерывна в каждой точке интервала (,),<и в точке = она непрерывна справа, а в точке = – слева, то она называетсянепрерывной на отрезке [,].

Все основные элементарные функции непрерывны в своих областях определения. Напомним, что под основными элементарными функциями понимают следующие пять функций:

1. степенную =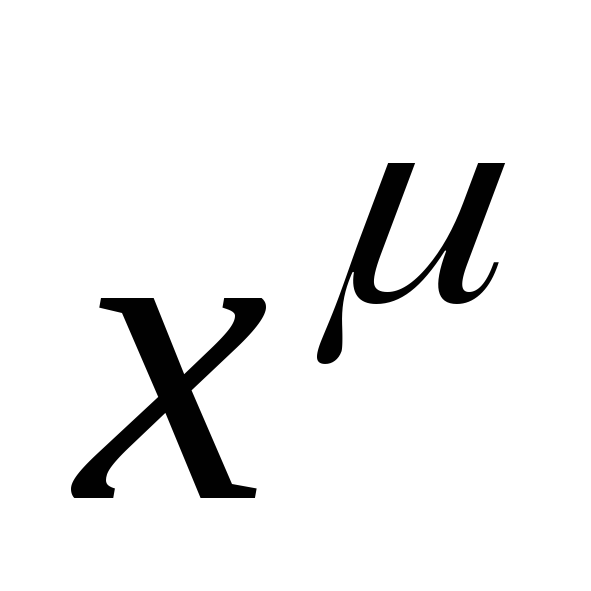, R;

2. показательную = , > 0, 1;

3. логарифмическую =, 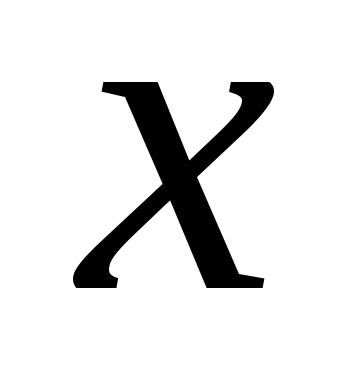> 0, > 0, 1;

4. тригонометрические =sin, =cos;

5. обратные тригонометрические=arcsin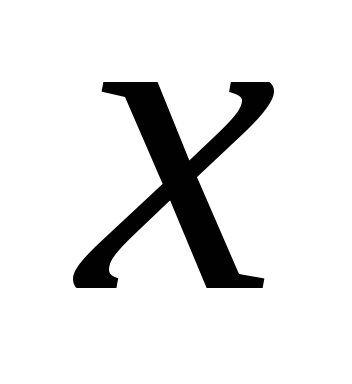, [–1, 1],

Типовой пример

Исследовать функцию на непрерывность.

►–точка разрыва. не существует, в других точках.,,– устранимый разрыв.

Функцию в точке можно доопределить

. ◄

Типовой пример

Найти точки разрыва функции и определить их вид.

.

►Пусть . Имеем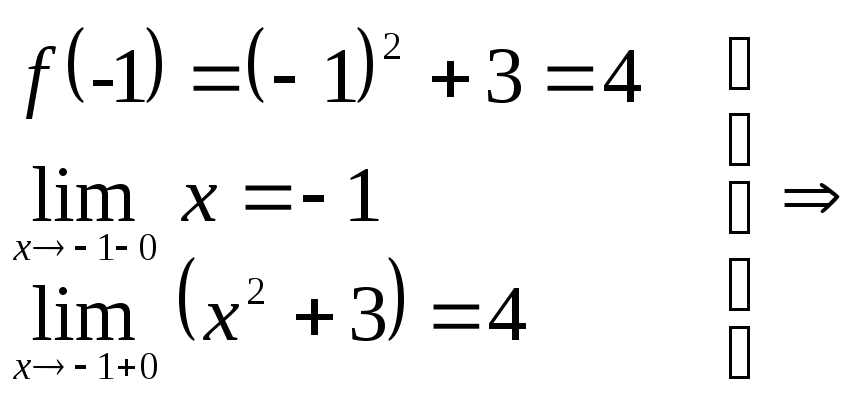в точкеразрыв первого рода.

Пусть . Имеемв точкефункция непрерывна. ◄

Типовой пример

Исследовать функцию на непрерывность

в точках и.

►1) – функция непрерывна.

2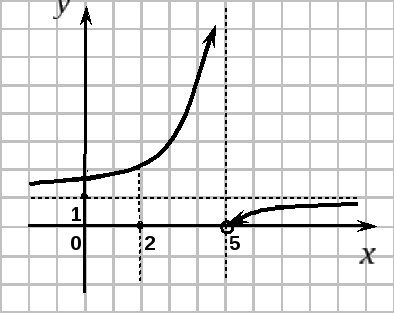)не существует – следовательно,- точка разрыва

; ..

Имеем разрыв II рода.◄

Типовой пример

Исследовать функцию на непрерывность. Построить график функции. Указать точки разрыва функции, если они существуют.

.

►В интервалах функция непрерывна. Исследуем на непрерывность функцию в точкахи.. Приимеем:.Таким образом, в точке х=0 функция непрерывна. Прифункция имеет разрыв 1-го типа. Строим график функции, выбирая удобный масштаб:◄

Типовой пример

Указать значения параметров a и b, при которых функция

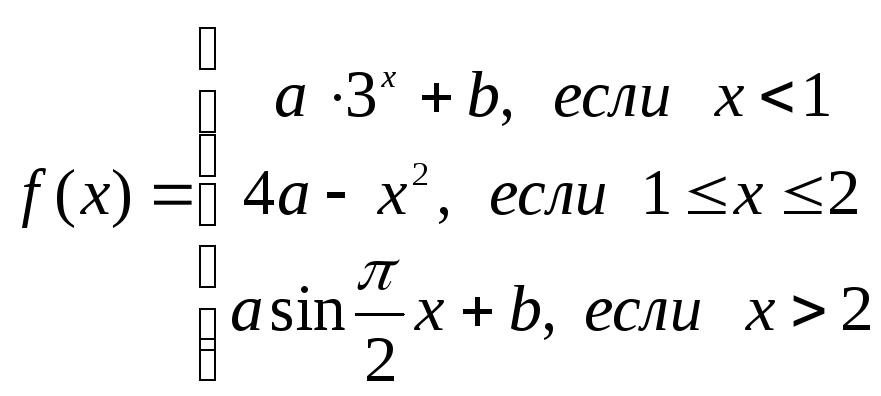непрерывна.

►Функция может иметь точки разрыва лишь в точках x₁=1 и x₂=2. Чтобы функция была непрерывна в этих точках, односторонние пределы в каждой из этих точек должны быть равны. Имеем:

,,

,.

Получаем систему уравнений:

.

Итак, при а=1 и b=0 получаем непрерывную функцию

.◄