3. Бесконечно малые величины и их сравнение

Функция называется бесконечно малой при(или), если(или). Так как, то при-бесконечно малая. Однако не является бесконечно малой при, так какОдна и та же функция может быть бесконечно малой или не быть в зависимости от предельного значенияx₀. Есть функции, например, x²+1, которые не могут быть бесконечно малыми ни при каких условиях.

ТЕОРЕМА 1. Сумма конечного числа бесконечно малых функций есть функция бесконечно малая.

ТЕОРЕМА 2. Произведение бесконечно малой в точке =функциина ограниченную в этой точке функциюесть функция бесконечно малая.

ТЕОРЕМА 3. Если — бесконечно малая в точке=и не обращается в нуль в некоторой окрестности этой точки, то= – бесконечно большая функция в этой точке.

Лемма. Для того, чтобы число было пределом функциив точке=, необходимо и достаточно, чтобы разность–была бесконечно малой в этой точке.

Пусть и– бесконечно малые функции в точке.

Определение 1. Если = 0, то функциюназываютбесконечно малой более высокого порядка малости по сравнению с и пишут=o() при  .

Определение 2. Если =c  0, то иназывают бесконечно малымиодного порядка малости и пишут =O() при  . В частности, если=c  0, то говорят, что имеет k-й порядок малости по сравнению с при  . Действительное числоk называют порядком малости, а сравнивают чаще всего с функцией = – .

Типовой пример

Пусть . Сравнить бесконечно малыеи.

►Рассмотрим предел отношения данных бесконечно малых.

Так как , то.

Так как , тоесть бесконечно малая 2-го порядка относительно.◄

Определение 3. Если = 1,иназываютсяэквивалентными, или асимптотически равными бесконечно малыми в точке . Пишут~ при  0

Если =+o, A  0, > 0, то выражениеназываетсяглавной степенной частью бесконечно малой функции в точке = .

ТЕОРЕМА. Если ~,~при  исуществует, то=.

Отметим также: если , то.

Основные формулы эквивалентности бесконечно малых

Известна формула первого замечательного предела:

_. Используя это равенство, получим _,

_{, ,}

_.

Отсюда получаем первую группу формул эквивалентности бесконечно малых.

При . (1)

Вторая группа формул связана с логарифмической функцией.

Имеем:

_,.

Если при , тои получаем вторую группу формул:

_, (2) Третья группа формул связана с показательной функцией. Имеем:

_. Отсюда _.

Тогда _{, ,}

_.

Итак, третья группа формул эквивалентности бесконечно малых

,,,(3)

.

Четвертая группа формул связана со степенной функцией.

Имеем: ,

.

Итак, четвертая группа формул эквивалентности бесконечно малых

,,,

,,, (4)

_,

_{, .}

Все эти четыре группы формул составляют таблицу эквивалентных бесконечно малых.

Типовые примеры

Найти пределы функций.

1) _.

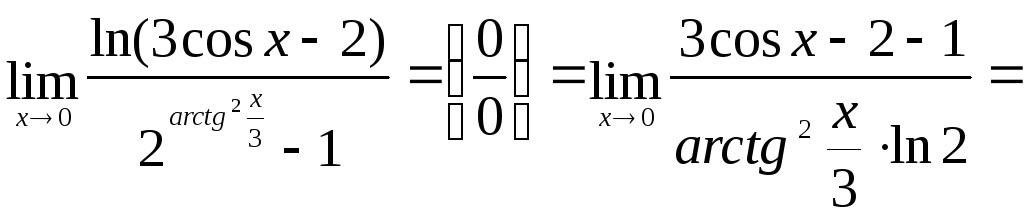
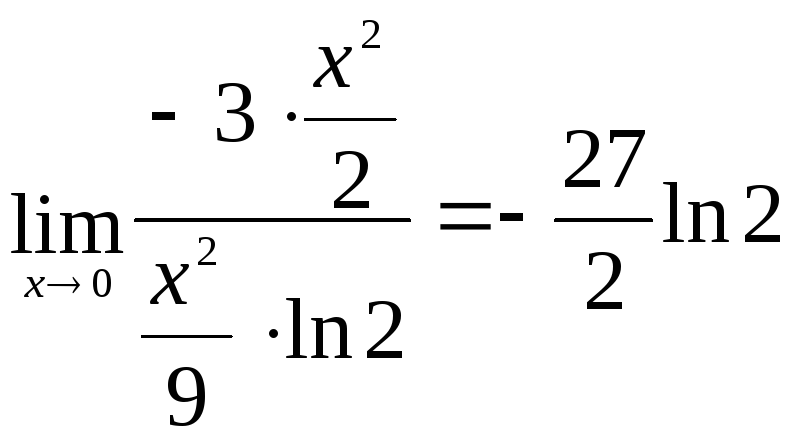►. Здесь при и поэтому применяем формулу из группы (2) . Так как, то применяем формулы и.◄

2) _.

►

.◄

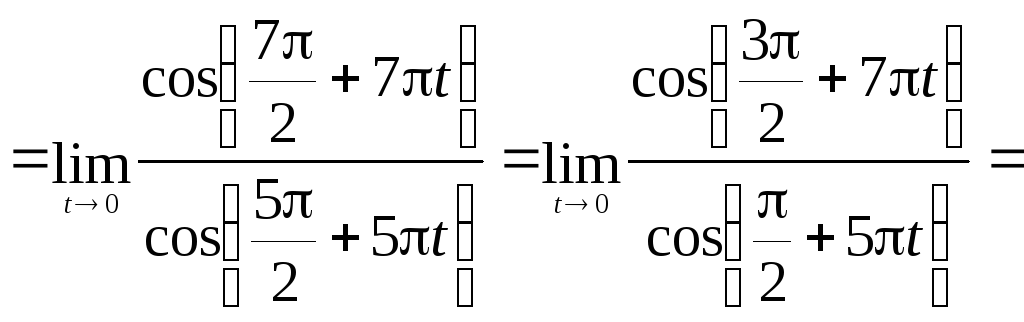
3) _.

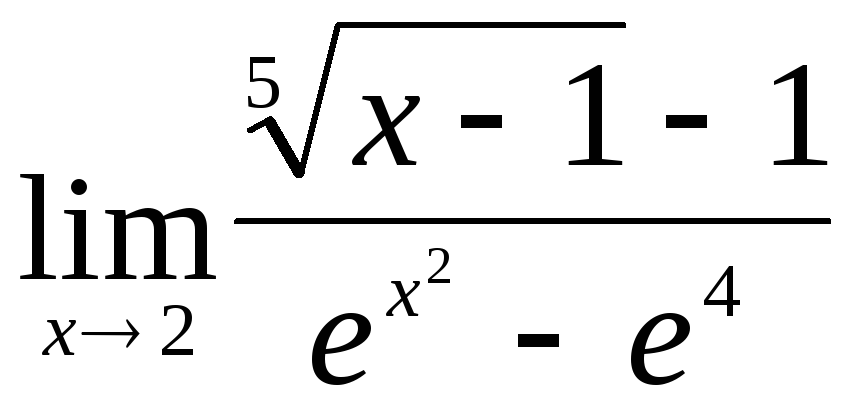►_.Здесь применены формулы .◄

4) .

► ◄

5) .

►. Имеем

,

, ,. Учитывая это, получаем

= .◄

6) .

►Имеем ~ = , ~. Отсюда находим ===

= ==.◄

Следует помнить, что принцип эквивалентности не всегда можно применять. Это прежде всего касается случая, когда эквивалентность применяют к сумме. Так, если при применять эквивалентность к выражениюtgx-sinx, то получите не переменную, а 0. По этой же причине нельзя применять эквивалентность при в выражениях,. Как быть в таком случае? Надо данные выражения путем элементарных преобразований привести к виду, где можно применить эквивалентность.

Отметим, что все формулы эквивалентности можно использовать для приближенных вычислений.

Типовой пример

Вычислить приближенно.

1)

► Имеем . Тогда.◄

2) ln 0,95.

► . Применена формула .◄

3) cos 0,1.

► . Применена формула .◄