
- •Глава I . Функции. Пределы.
- •§1. Числовые множества
- •1. Множества и операции над ними
- •2. Декартово произведение. Соответствия
- •4. Числовые промежутки
- •5. Границы числовых множеств
- •§2. Функции действительной переменной
- •1. Отображение
- •2. Основные характеристики функции
- •§3. Пределы
- •1. Предел числовой последовательности
- •2. Предел функции
- •Для определения пределов последовательностей и функций используются некоторые известные приемы.
- •3. Бесконечно малые величины и их сравнение
- •§4. Непрерывность функции
- •1. Непрерывность функции в точке
- •2. Точки разрыва функции
- •3. Свойства непрерывных функций
- •Последовательности в экономических задачах
- •1. Задачи о непрерывном начислении процентов
- •2. Потоки платежей. Финансовая рента
- •3. Рекуррентное уравнение динамики основного капитала
- •4. Паутинообразная модель рынка
- •Вопросы промежуточного контроля
2. Предел функции
К элементарным
функциям
относятся: 1) простейшие
элементарные функции:
постоянная с, степенная
![]() ,
показательная
,
показательная![]() ,
логарифмическая
,
логарифмическая![]() ,
тригонометрическая
,
тригонометрическая![]() ,
обратные тригонометрические
,
обратные тригонометрические![]() ;
2) всефункции,
получающиеся из простейших элементарных
функций
путем применения конечного числа
следующих четырех операций: сложение,
умножение, деление, суперпозиция функций
(сложная функция). В класс элементарных
функций попадают: а) многочлен; б)
рациональная дробь (отношение двух
многочленов); в)
;
2) всефункции,
получающиеся из простейших элементарных
функций
путем применения конечного числа
следующих четырех операций: сложение,
умножение, деление, суперпозиция функций
(сложная функция). В класс элементарных
функций попадают: а) многочлен; б)
рациональная дробь (отношение двух
многочленов); в)![]() ,
т.к.
,
т.к.![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ,
т.к.
,
т.к.![]() ,
и множество других.
,
и множество других.
Пусть
функция
![]() определена во всех точках интервала
определена во всех точках интервала![]() ,
за исключением, быть может, точки
,
за исключением, быть может, точки![]() .
Число А называетсяпределом
функции
.
Число А называетсяпределом
функции
![]() в точке
в точке![]() ,
если для любого
,
если для любого![]() существует число
существует число![]() такое, что для любогоx,
удовлетворяющего неравенству
такое, что для любогоx,
удовлетворяющего неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство![]() ,
при этом пишут
,
при этом пишут![]() .
Можно дать другое, равносильное
приведенному, определение: числоA
называется пределом функции
.
Можно дать другое, равносильное
приведенному, определение: числоA
называется пределом функции
![]() в точкеx0,
если для любой последовательности чисел
в точкеx0,
если для любой последовательности чисел
![]() ,
сходящейся к
,
сходящейся к![]() ,
,![]()
![]() .
Если
.
Если![]() определена в интервале
определена в интервале![]() ,то
числоA
называется пределом
,то
числоA
называется пределом
![]() при
при
![]() ,если
для любого
,если
для любого
![]() существует число
существует число![]() ,
такое, что неравенство
,
такое, что неравенство![]() влечет за собой неравенство
влечет за собой неравенство![]() .
При этом пишут
.
При этом пишут![]() или
или![]() .
Аналогично определяется
.
Аналогично определяется![]() .
.
Типовые примеры
Доказать (найти
![]() ,
что:
,
что:
1)
![]() ,2)
,2)![]() .
.
1)
►Надо доказать, что для
![]() ,
для которых
,
для которых![]() ,
выполняется неравенство
,
выполняется неравенство![]() для
для![]() .
Имеем:
.
Имеем:
![]()
Примем
![]() .
Тогда
.
Тогда![]() .
Итак, для
.
Итак, для![]()
![]() такое, что
такое, что![]() для
для![]() ,
для которых
,
для которых![]() .◄
.◄
2)
►Пусть
![]() ,
,![]() .
Тогда
.
Тогда![]() .
Здесь в числителе пользуемся неравенством
.
Здесь в числителе пользуемся неравенством![]() а в знаменателе пользуемся неравенством
а в знаменателе пользуемся неравенством
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда![]() .
Итак, для
.
Итак, для![]()
![]() такое, что неравенство
такое, что неравенство![]() выполняется для всехx,
для которых
выполняется для всехx,
для которых
![]() .◄
.◄
Число A
называют пределом
функции
![]() в точке
в точке
![]() слева (справа)
и пишут
слева (справа)
и пишут
![]() или
или![]()
![]() ,
или
,
или![]() ,
если для любого
,
если для любого![]() найдется
найдется![]() такое, что для
такое, что для![]()
![]() (для
(для![]()
![]() )
справедливо неравенство
)
справедливо неравенство![]() .
ЧислоA
является пределом
.
ЧислоA
является пределом
![]() в точке
в точке![]() ,
если совпадают пределы
,
если совпадают пределы![]() в этой точке слева и справа:
в этой точке слева и справа:![]() .
.![]()
Если функция
![]() определена в интервале
определена в интервале![]() (в интервале
(в интервале![]() ) и для любогоM
существует
) и для любогоM
существует
![]() такое, что для любого
такое, что для любого![]() (для любого
(для любого![]() справедливо неравенство
справедливо неравенство![]() ,
то говорят, что левый (правый) предел
функции
,
то говорят, что левый (правый) предел
функции![]() в точке
в точке![]() равен
равен![]() ,
и при этом пишут
,
и при этом пишут![]() или
или![]()
![]() или
или![]() Аналогично определяются
Аналогично определяются![]() и
и![]() .
.
Предел функции
обладает теми же свойствами, что и предел
последовательности: если
![]() ,
,![]() ,
то
,
то
(последнее при
![]() ).
То же верно для односторонних пределов.
).
То же верно для односторонних пределов.
Имеют место равенства
![]() ,
,
![]() ,
,
называемые первым и вторым замечательными пределами. Можно доказать, что
1)![]()
![]() = e, 4)
= e, 4)
![]()
![]() =
=
![]() ,
,
2)
![]()
![]() =
=
![]() , 5)
, 5)
![]()
![]() = 1,
= 1,
3)
![]()
![]() = 1, 6)
= 1, 6)
![]()
![]() =
=
![]() .
.
Заметим, что если
![]() то в указанных равенствах можно заменитьx
на
то в указанных равенствах можно заменитьx
на
![]()
Например,
![]()
При нахождении
пределов вида
![]() следует иметь в виду, что:
следует иметь в виду, что:
1)если существуют
конечные пределы
![]() и
и![]() ,
то
,
то![]() ;
;
2)если
![]() и
и![]() ,
то вопрос о нахождении данного предела
решается непосредственно, при этом
помним, что
,
то вопрос о нахождении данного предела
решается непосредственно, при этом
помним, что и
и ;
;
3)если
![]() и
и![]() ,
то полагают
,
то полагают![]() ,
где
,
где![]() при
при![]() и, следовательно,
и, следовательно,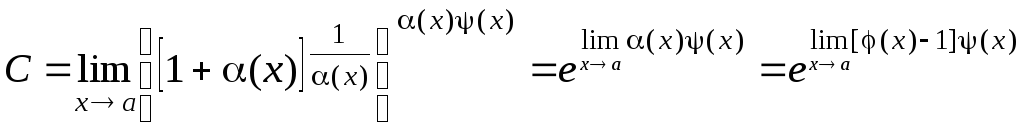 ,
где
,
где![]() .
.
Для определения пределов последовательностей и функций используются некоторые известные приемы.
Типовые примеры
1)
![]() .
.
►Если необходимо
найти предел
![]() ,
можно предварительно привести к общему
знаменателю
,
можно предварительно привести к общему
знаменателю
![]() .
.
Поделив на член, имеющий максимальную степень, получим в числителе постоянную величину, а в знаменателе – все члены, стремящиеся к 0,то есть
 .◄
.◄
2)
![]()
►Данный пример решается аналогично предыдущему:
 ◄
◄
3)
![]() .
.
►При подстановке
![]() ,
получим
,
получим![]() .◄
.◄
4)
![]() .
.
►В этом пределе,
если подставить
![]() ,
то получится неопределенность, которую
можно преодолеть, если разложить разность
кубов в знаменателе
,
то получится неопределенность, которую
можно преодолеть, если разложить разность
кубов в знаменателе![]() ,
а числитель в виде:
,
а числитель в виде:
![]() .
.
Тогда
![]() и подставив
и подставив
![]() ,
получим:
,
получим:
![]() .◄
.◄
5)
![]() .
.
►Если необходимо
найти предел рациональной функции
![]() ,
то при делении на член с минимальной
степенью, получим
,
то при делении на член с минимальной
степенью, получим![]() ;
и, устремив
;
и, устремив![]() к 0, получим:
к 0, получим:
![]() .◄
.◄
6)
![]() ►Имеет
место неопределенность вида
►Имеет
место неопределенность вида
![]() Так как
Так как![]() является корнем многочленов из числителя
и знаменателя, то
является корнем многочленов из числителя
и знаменателя, то![]() выделяется как сомножитель в числителе
и знаменателе. Для разложения на множители
выполним деление «уголком» Имеем
выделяется как сомножитель в числителе
и знаменателе. Для разложения на множители
выполним деление «уголком» Имеем
![]() ◄
◄
Если в пределах содержатся иррациональные выражения, то приходится вводить новые переменные для получения рационального выражения, или же переводить иррациональности из знаменателя в числитель и наоборот.
7)
![]() .
.
►Сделаем замену
переменной. Заменим
![]() ,
при
,
при![]() ,
получим
,
получим .◄
.◄
8)
![]() .
.
►Если числитель
и знаменатель умножить на одно и то же
число, то предел не изменится. Умножим
числитель на
![]() и разделим на это же выражение, чтобы
предел не изменился, а знаменатель
умножим на
и разделим на это же выражение, чтобы
предел не изменился, а знаменатель
умножим на![]() и разделим, на это же выражение. Тогда
получим:
и разделим, на это же выражение. Тогда
получим:
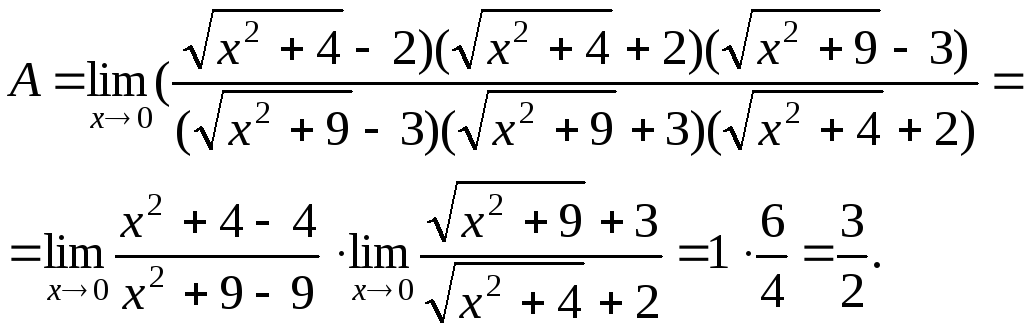 ◄
◄
9)
![]() .
.
►![]() [
[![]() ]=(Умножим
числитель и знаменатель на выражение,
сопряженное числителю) =
]=(Умножим
числитель и знаменатель на выражение,
сопряженное числителю) =
 ◄
◄
10)
![]()
►Имеет место
неопределенность вида
![]() Произведем замену
Произведем замену![]() Тогда при
Тогда при![]()
 ◄
◄
11)
![]() .
.
►Для вычисления
такого предела сведем его к 1-му
замечательному пределу. Для этого
умножим и разделим числитель на
![]() ,
а знаменатель на
,
а знаменатель на![]() ,
тогда
,
тогда .◄
.◄
12)
![]() .
.
►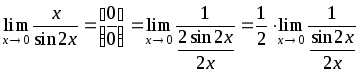 =
[ по первому замечательному пределу ] =
=
[ по первому замечательному пределу ] =
![]() ◄
◄
13)
![]() .
.
►
◄
14)![]() .
.
►Для вычисления
этого предела сведем его ко второму
замечательному пределу. С этой целью
из рационального выражения в скобках
выделим целую часть и представим ее в
виде правильной дроби. Так поступают в
тех случаях, когда
![]() ,
где
,
где![]() ,
а
,
а![]() ,
где
,
где![]() ;
;
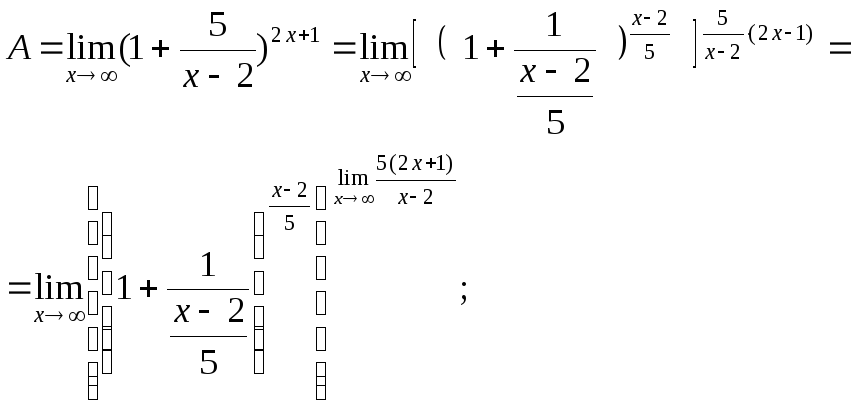
 , а
, а
![]() ,
то окончательно
,
то окончательно![]() .
Здесь использовалась непрерывность
композиции непрерывных функций. ◄
.
Здесь использовалась непрерывность
композиции непрерывных функций. ◄
15)
► =[
по второму
замечательному пределу
] =
=[
по второму
замечательному пределу
] =
 ◄
◄
16)
![]() .
.
►
◄
17)![]() .
.
►Имеем
 и
и![]() .
Поэтому
.
Поэтому![]() .◄
.◄
18) Найдите
![]() и
и
![]() ,
если
,
если
 .
.
► Рассмотрим
нахождения левого и правого пределов.
Пусть
 Если
Если![]() Следовательно,
Следовательно,![]() Если же
Если же![]()
![]() и
и
![]()
Таким образом,
![]() Это означает, что не существует
Это означает, что не существует![]() ◄
◄
