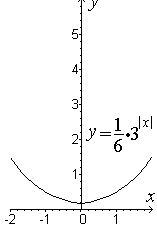§2. Функции действительной переменной

1. Отображение

Мы говорим, что задано отображение множестваво множество, и пишем, если каждому элементуиз области определениясопоставлен однозначно определенный элементиз области действия, называемыйобразом элемента при отображении(такое сопоставление символически принято обозначать так:). При этом не исключается возможность, что одному элементуотвечает при отображениинесколько элементов, таких, что. Подмножествовсех таких элементов называетсяпрообразом элемента при отображениии обозначается, т.е..

Более общо, образом множества при отображенииназывается множество.Прообразом множества при отображении(обозначают:) называется объединение прообразов всех элементов, входящих в, т.е.

.

Отображение называют такжепреобразованием множества (в себя). Вместо термина «отображение» часто употребляют термин «оператор» (особенно в функциональном анализе и линейной алгебре). а также «функция» (особенно в случае, когда– числовое множество).

Переменную называютаргументом или независимой переменной, а переменную –зависимой переменной от х; множество –областью определения функции , а множество–множеством значений функции ,– закон соответствия.– множество значений аргумента, при которых формулаимеет смысл.

Кроме буквы для обозначения функций используют и другие буквы греческого и латинского алфавитов:,,,и так далее.

Примеры

1) ,.

2) ,.

3) или,.

4) ,.

Если элементами множеств иявляются действительные числа, то функция называетсячисловой.

Частное значение функции при обозначают так:.

Пример

График функции – это множество точек плоскости с координатами, где, для каждой из которыхявляется значением аргумента, аявляется соответствующим значением функции.

2. Основные характеристики функции

Функция , определенная на множестве, область определения которой симметрична относительно начала координат, называется:четной, если выполняются условияи;нечетной, если выполняются условияи. В противном случае функцияназывается функциейобщего вида.

График четной функции симметричен относительно оси , график нечетной функции симметричен относительно начала координат.

Например, функция - четная, а функция–функция общего вида.

Пусть функция определена на множестве, интервал.

Если для любых ииз интервала, причем, выполняется неравенство:

1) , то функцияназываетсянеубывающей на ;

2) , то функцияназываетсяневозрастающей на ;

3) , то функцияназываетсявозрастающей на ;

4) , то функцияназываетсяубывающей на .

Во всех рассмотренных случаях функции называютсямонотонными, а возрастающая и убывающая функции строго монотонными.

Пример

На рисунке функция настрого монотонная; намонотонная.◄

Типовой пример

Докажите, что функция строго убывает, если .

►Функция строго убывает на , если для любых значений и из этого полуинтервала таких, что, следует, что.

Рассмотрим разность:

так как при и, кроме того, выполнены условия; в силу . Итак, мы доказали, что для любых значений аргументов из промежутка , из условия , следует, чтот.е. функция строго убывает на .◄

Функция , определенная на множестве, называетсяпериодической на этом множестве с периодом , где– положительное число, если выполняются условия:и. Если– период, то периодом функции также будут числа, где

Пример

Для функции периодами будут числа

Функция, определенная на множестве, называетсяограниченной на этом множестве, если существует такое число , что для всехвыполняется неравенство. Коротко можно

записать так:

.

График ограниченной функции расположен между прямыми и. Например, функцияограничена, так как.

3. Классификация функций и построение графиков

Отображение называетсясюръективным (или отображением «на»), если каждый элемент из имеет, по крайней мере, один прообраз, т.е..

Примерами сюръективных отображений являются функции,.

Отображение называетсяинъективным (или вложением), если из следует, т.е. каждый образобладает ровно одним прообразом.

Примерами инъективных отображений могут служить монотонные функции,,и т.д.

Отображение называетсябиективным, если оно одновременно и инъективно и сюръективно.

Обратимость отображений

Пример

Пусть зависимость спроса от цены при прочих неизменных условиях определяется уравнением . Если требуется определить, при каком значении цены спрос будет равен 80, то в этом случае мы решаем обратную задачу: по значению функции определяем значение аргумента. ◄

Пусть . Рассмотрим уравнение, порожденное отображением:

, (1)

где – неизвестное,– параметр.

Ясно, что если инъективно, но не сюръективно, то существуют такие значения параметра, при которых уравнение (1) не имеет решений, а для тех значений параметра, при которых у уравнения есть решения, это решение для каждого значения параметра единственно.

Если сюръективное отображение, но не инъективное, то уравнение (1) имеет решения при любом значении параметра, и существует хотя бы одно такое значение параметра, при котором уравнение (1) имеет более одного решения.

В случае, когда – биективное отображение, уравнение (1) имеет при каждом значении параметра единственное решение. В этом случае отображениеопределяет другое отображение, которое каждому элементуставит в соответствие решение уравнения (1). Это решение обозначается. Отображениеназывается обратным для отображения.

Нетрудно убедиться, что и.

Отображение называетсяобратимым, если существует отображение такое, что

, ,

, .

При этом отображение называетсяобратным к .

ТЕОРЕМА (критерий обратимости). Для того чтобы отображение было обратимым, необходимо и достаточно, чтобы оно было биективным.

Примеры

1) не является обратимым;

2) не является обратимым;

3) не является обратимым;

4) обратим,.

Таким образом, чтобы найти функцию=, обратную к функции , достаточно решить уравнениеотносительно. Традиционно независимую переменную обозначают, а зависимую. Итак, если уравнениеможно разрешить относительно, то полученное явное выражение задает функцию, обратную по отношению к функции . При этом для всех допустимых значенийвыполнено соотношение.

Пример

Функции ивзаимно обратные. Графики их симметричны относительно биссектрисыI и III координатных углов.

Из определения обратной функции следует, что для любой строго монотонной функции существует обратная. При этом если возрастает, то итакже возрастает. Например, функциянастрого возрастает. На этом промежутке существует обратная ей функция, которая также возрастает.

Пример

В формуле функции спроса ценаявляется аргументом, а количество товара, которое покупатели готовы приобрести ‑ функцией. Разрешив уравнение функции спроса относительно переменной , получим функцию, обратную данной:. Эта функция определяет максимально возможную цену, при которой товар в количестве может быть продан на рынке. ◄

Композиция функций (сложная функций)

Пусть ,.Композицией (или суперпозицией) функций иназывается функция, обозначаемаяи определяемая следующим равенством:

.

Правая часть этого равенства показывает, что значение композиции в точке вычисляется в результате последовательного действия сначала, а затем (на полученный результат) функции.

Пример

Пусть и,и. Тогда,. Попутно мы доказали, что во множестве функций, на которых определены ии, композиция не является коммутативной операцией.

Основные элементарные функции и их графики

Основными элементарными функциями называют следующие функции.

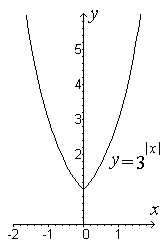
1. Степенная функция ,.

Примеры графиков степенных функций, соответствующих различным показателям степени, показаны на рисунках.

2. Показательная функция ,,.

На рисунке показаны графики функций, соответствующие различным основаниям.

3. Логарифмическая функция ,,.

Графики логарифмических функций, соответствующие различным основаниям логарифма, показаны на рисунке.

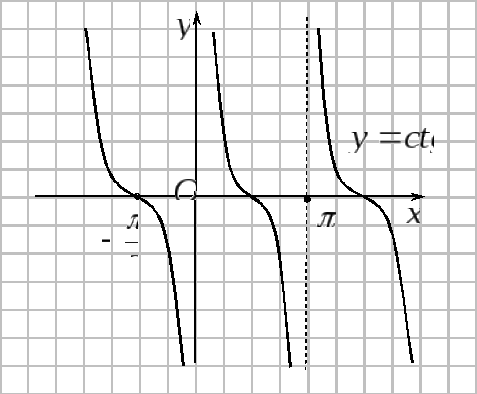
4. Тригонометрические функции ,,,.

Графики тригонометрических функций показаны на рисунках.

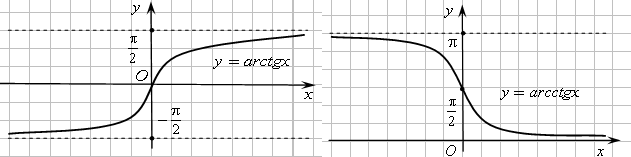
5. Обратные тригонометрические функции ,,,.

Графики обратных тригонометрических функций показаны на рисунках

Все функции, получаемые из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными функциями.

Пример

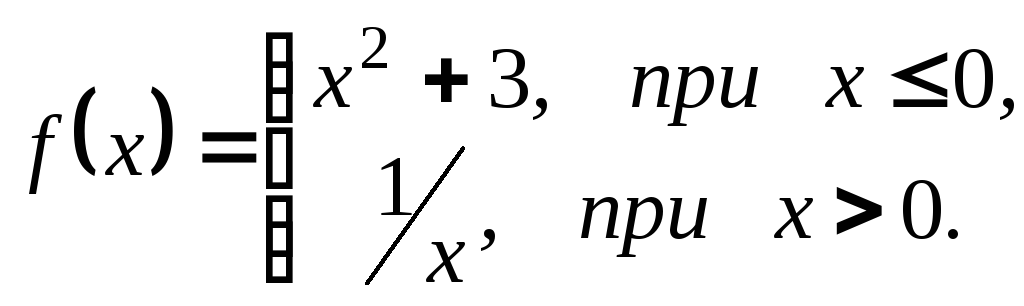Функции ,,– элементарные; функцияне является элементарной.В качестве примера неэлементарной функции укажем модуль действительного числа x

Напомним, что графиком функции называется множество точек плоскости с координатами (x, ), где. Из определения функции следует, что график функцииимеет ровно одну точку пересечения с вертикальной прямойx = a для любого элемента На рис. (а) изображен график функцииy=| x |, а на рис. (б) - пример кривой L, не являющейся графиком никакой функции.

а	б

Правила преобразования графиков функций

ФУНКЦИЯ	ДЕЙСТВИЯ С ГРАФИКОМ	ДЕЙСТВИЯ С ОСЯМИ
	Переместить график наединиц по оси(вверх прии вниз при)	Перенести ось абсцисс на единиц вниз при(вверх при).
	Переместить график наединиц по оси (вправо при , влево при).	Перенести ось ординат на единиц (влево при, вправо при).
	Отобразить график симметрично относительно оси абсцисс (оси)(иногда говорят о «зеркальном» отображении).
	График отобразить симметрично относительно оси ординат (оси).
	Увеличить ординаты «базового» графика в раз приили уменьшить враз при
	У базового графика уменьшить абсциссы в раз приили увеличить их враз при
	Оставить график без изменения там, где; фрагменты графика, соответствующие условию, отобразить симметрично относительно оси.

Типовые примеры

Построить графики данных функций, исходя из основных элементарных функций. Указать их области определения и области значений. Проверить, являются ли функции четными, нечетными или периодическими. В случае периодичности найти период:

►1) . Преобразуем данную функцию к видуВ качестве исходного возьмем график функцииИмеемk=2 (сжатие в 2 раза вдоль оси Ox); раза вдоль оси Oy c последующей симметрией относительно оси Ox ).

На рисунке изображены последовательные преобразования, приводящие к построению искомого графика.

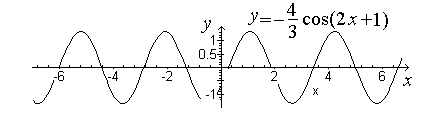
Очевидно, что данная функция определена на всей числовой прямой, т.е. и для всех x, т.е.

Так как график не симметричен ни относительно оси Ox, ни относительно начала координат, функция не является ни четной, ни нечетной. Из периодичности функции с периодомследует периодичность данной функции с периодом

2) .

►Построим сначала график функции . Так как |-x| = |x|, то эта функция четная, и ее график получается из графика функции симметрией относительно осиOy и сжатием в 6 раз вдоль оси Oy, поскольку .

Искомый график образуется из полученного графика сдвигом на 2 единицы вправо, так как а=2.

Поскольку график функции не симметричен ни относительно осиOy, ни относительно начала координат, функция не является ни четной, ни нечетной. По графику видно, что функция непериодична,

3) С помощью преобразования графика гиперболы построить график функции.

►Сначала необходимо выделить «целую часть» данной дробно-рациональной функции: .

Далее последовательно выполняются следующие действия:

1) построить график функции ;

2) сдвинуть его на 3 единицы влево по оси OX (получить график функции );

3) полученный график симметрично отобразить относительно оси OX (график функции );

5) сдвинуть его на единицу вверх вдоль оси OY (график заданной функции).

Результат построений можно видеть на рисунке 1.1.