§3. Пределы

1. Предел числовой последовательности

Числовой последовательностью называют правило, по которому каждому натуральному числу ставится в соответствие действительное (комплексное) число. Последовательность обозначают символом(). Можно сказать, что последовательность является функцией().Числовую последовательность задают формулойn-го члена: . Например, еслито, , ... и т.д.

Числовую последовательность также можно задать рекуррентным соотношением: ,. Тогда ,, и т.д.

Пример

Арифметическая прогрессия ‑ числовая последовательность, в которой каждый член, начиная со второго, отличается от предыдущего на одно и то же число , называемое разностью прогрессии:. Любая арифметическая прогрессия имеет вид Общий член арифметической прогрессии определяется так: .

Арифметическая прогрессия применяется при выполнении финансово-коммерческих расчетов, когда при начислении дивидендов, прибыли и т.д. используются простые проценты .

Пример

Первого марта 2008 г. некто положил в банк сумму в 500 тыс. рублей из расчета 60 процентов годовых. Известно, что сумма вклада растет линейно (простые проценты). Какова сумма вклада на 1 июля того же года?

►Для ответа на поставленный вопрос обозначим через сумму вклада в начальный момент (в данном случае 1-го марта), через год и на момент времени соответственно. Тогда из условия задачи получаем , где- учетная ставка (в данном случаеa = 0,6). Из полученного уравнения следует, что . Значение суммы вклада на момент времени можно получить из уравнения прямой, проходящей через две точки и:

,

откуда следует , где. Поскольку в данном примере=, то значение суммы вклада на 1 июля составит 500(1+0,61/3) = 5001,2 = 600 (тыс.руб.). ◄

Пример

Геометрическая прогрессия ‑ числовая последовательность, в которой каждый член, начиная со второго, отличается от предыдущего на один и тот же множитель , называемый знаменателем прогрессии. Любая геометрическая прогрессия имеет вид Общий член геометрической прогрессии определяется по формуле .

Геометрическая прогрессия применяется при выполнении финансово-коммерческих расчетов, когда при начислении дивидендов, прибыли и т. д. используются сложные проценты.

Пример

Банк ежемесячно производит перерасчет суммы вклада, начисляя дополнительную сумму, пропорциональную значению текущего счета. Через сколько месяцев первоначальная сумма вклада удвоится?

►Обозначим через исумму вклада в начальный момент и через месяцев соответственно. Тогда по условию задачи имеем:

, , ,

где ‑ заданная учетная ставка (100%, если учетная ставка измеряется в процентах). Таким образом, последовательные значения суммы вклада на конец -го месяца образуют геометрическую прогрессию, общий член которой имеет следующий вид:

.

Из полученного соотношения следует, что если , то для нахождения соответствующего значения нужно решить уравнение . Логарифмируя это уравнение по основаниюе, получим , откуда следует . Если, например, ежемесячно начисляется 5%, то=0.05, и для получаем=14.2. Итак, через 15 месяцев сумма вклада увеличится более чем вдвое (через 14 месяцев она увеличится в 1.05¹⁴=1.98 раз, а через 15 месяцев ‑ в 2.08 раз по сравнению с первоначальной).◄

Очевидным образом определяются сумма, произведение, частное двух последовательностей. Мы будем иметь дело лишь с последовательностями действительных чисел.

Число называетсяпределом последовательности если для любогонайдётся номертакой, что для любоговыполняется неравенство. При этом пишутилии говорят, что последовательностьсходится к числу.

Геометрически это означает, что для любой O (,) найдётся такой номер, что всеприn > будут принадлежать этой–окрестности. (> 0 (n >   O (,))). Если=C = const, то =C, т.к. = 0 <для любыхn.

Чтобы найти предел последовательности, используя только его определение, следует поступить так:

1. предположить, что предел равен ;

2. решить неравенство <относительноn для любого > 0;

3. если решение неравенства имеет вид n > , то предположение, что предел равен, верно и предел найден.

ТЕОРЕМА 1. Если последовательность имеет предел, то он единственный.

Свойства предела.

Если ,, то:

1) ;

2) ;

3) ;

4) при ().

Последовательность называетсябесконечно малой, если .

Последовательность называетсябесконечно большой, если для любого найдётся номерn₀ такой, что для любого справедливо неравенство ; записывается это так:. Если при этом, начиная с некоторого номера, сохраняют положительный (отрицательный) знак, то пишут() . Если последовательность имеет конечный предел, то она называется сходящейся. В противном случае – расходящейся. Последовательность называетсянеубывающей, если  для любогоn. Если  , – то этоневозрастающая последовательность. Невозрастающая и неубывающая последовательности называются монотонными. Если неравенства строгие (<,>), то последовательности называются строго монотонными.

ТЕОРЕМА 2. Монотонная ограниченная последовательность сходится.

Важную роль играет последовательность Доказывается, что эта последовательность сходится, и ее предел обозначается буквой е; е2,718.

Типовой пример

Доказать, пользуясь определением предела последовательности, что .

►Имеем:

. Решив неравенство , получими ясно, что достаточно выбрать, чтобы длянеравенствовыполнялось для всех. Что и требовалось.

Типовой пример

Дана последовательность . Найдите: 1); 2)такое, что для всехвыполняется неравенство.

1) ►Имеем

.

2) ►Найдём требуемое . Из проделанных выше выкладок следует, чтодолжно быть подобрано так, чтобы для всех

или ; отсюда следует , . Следовательно, можно взять.

Предел отношения многочленов

Пусть x_n и y_n многочлены от n степени k и m соответственно, т.е.

x_n=P_k(n)=a₀ n^k+a₁n^k-1+...+a_k, y_n=Q_m(n)=b₀n^m+b₁n^m-1+...+b_m

Докажем, что предел отношения многочленов равен пределу отношения их старших членов, т.е.

.

Имеем: , что и требовалось.

Итак,

Типовые примеры

Найти пределы:

1)

►Раскроем скобки, приведем подобные и воспользуемся приемом из предыдущего примера

◄

2) . ►.◄

3). ►. ◄

4) . ►.◄

Следует отметить, что полученные формулы справедливы не только для многочленов целой степени, но и для многочленов дробной степени, так как для любогоa>0.

При вычислении пределов, в которых присутствуют суммы арифметической или геометрической прогрессии, используются формулы для суммы арифметической прогрессии идля суммы геометрической прогрессии.

Типовые примеры

1) .►◄

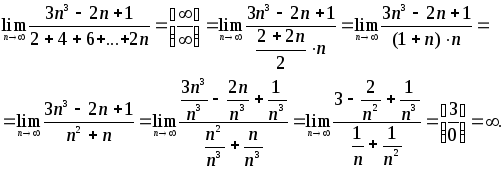2) .►

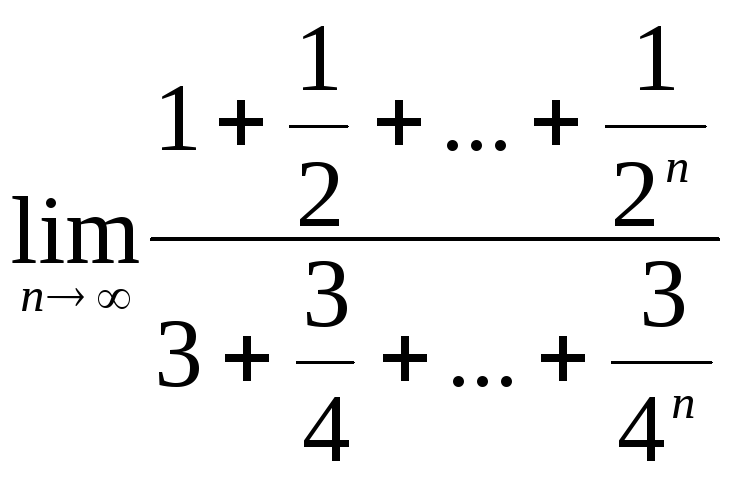=[используем формулу суммы геометрической прогрессии]= =◄

3) ►В данном выражении участвует функция n! (читается n-факториал), которая определяется равенством Имеем

,

◄

4) . ►В числителе три слагаемых соответственно степени:Следовательно, степень числителя равна, а главный член в числителе равен. Аналогично, главный член в знаменателеИмеем:.◄

5) . ►.◄

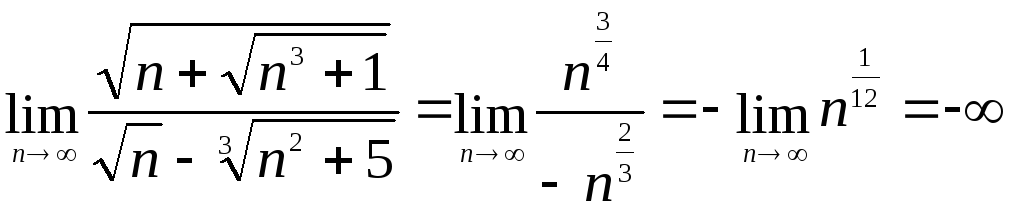6) . ►т.к.◄

7) . ►.

Как видите, идея о главном старшем члене здесь также дает быстрое решение.

Обычно этот предел вычисляется так:

◄

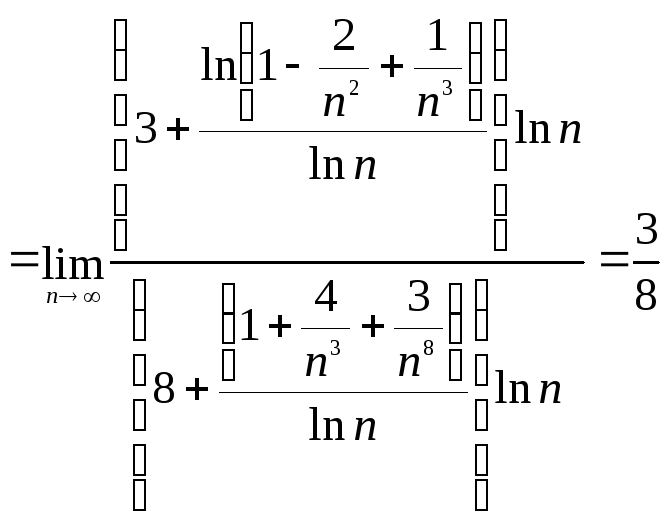8). ►

◄

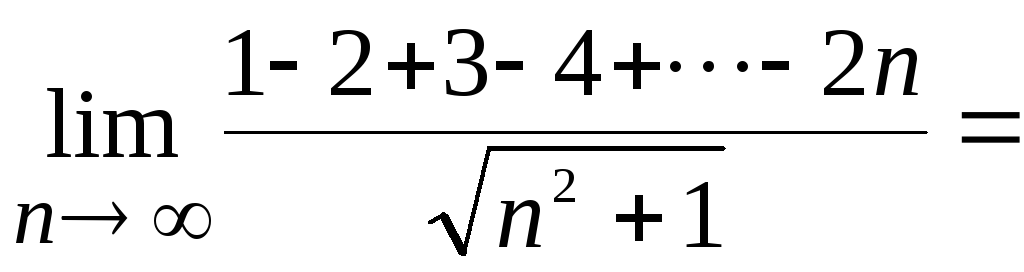
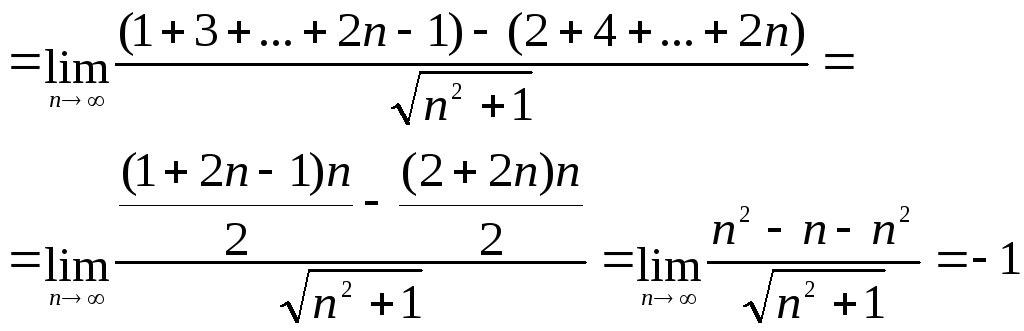9) . ► Напомним: . Имеем:

.◄

Для избавления от неопределенности здесь следует избавиться от иррациональности в числителе, умножив и разделив данное выражение на соответствующее сопряженное выражение.

Типовые примеры (неопределенности ).

1) . ►Используем формулу

Для данного примера

Имеем:

◄

2) . ►Напоминаем, чтои при.

Имеем:

=.◄

3) .

►

◄